Графические методы исследования.
В подразделе описаны виды относительных величин и методика их расчета. Вопросы для изучения: —Когда используются относительные величины? —Как адекватно выбрать вид относительной величины и графического изображения для характеристики явления? Цель - ознакомить со значением относительных величин для медицинской статистики; научить рассчитывать и адекватно использовать относительные величины в практике врача; научить графическому изображению относительных величин. Полученные во время исследования данные об отдельной единице совокупности подлежат первичной обработке — сведению в таблицы и группировке, после чего собранная информация подаётся в виде статистических показателей. Такие показатели уже носят обобщающий характер и в зависимости от признака, который исследуется, представляются через абсолютные, относительные и средние величины. Абсолютные величины — это характеристика всего исследуемого явления по отдельному признаку. Они есть результат первичного учета, первичной регистрации, в соответствующих учетных документах. В большинстве случаев абсолютные величины интересны и сами по себе, характеризуя, например, численность населения, число рождений, прирост населения, число врачей, число больничных коек или поликлинических посещений, количество различных инфекционных заболеваний и т. д.
Но неправильно было бы рассматривать абсолютные величины только как промежуточный этап, как сырье для получения производных величин и не считаться с их самостоятельным значением и ценностью. Кроме того, абсолютные числа необходимы для оперативного управления в здравоохранении. Например, из абсолютного числа рождений выходят при планировании родильных коек, из абсолютного числа детей — при планировании количестве мест в детсадах и школах, из численности населения — при расчетах числа больничных коек, поликлинических посещений, числа и категорийности санитарно эпидемиологических станций, при расчете необходимого медицинского персонала. И, наконец, без абсолютных чисел мы не можем оценить значение и достоверность относительных и средних чисел, а также невозможно вычислить средние ошибки. Однако в подавляющем большинстве случаев ряды абсолютных чисел мало доступны для обзора и недостаточны, а иногда совсем непригодны для сравнения - наиглавнейшей цели статистического анализа. Именно сравнение, сопоставление во времени, пространстве и для разных контингентов является основой выявления связей и закономерностей, оценки уровня, сдвигов и качественных особенностей, исследуемых процессов.
По абсолютным числам заболеваний или случаев смерти в разных городах или в отдельные годы нельзя судить о размерах заболеваемости и смертности, потому что это число может быть предопределено расхождениями в численном и возрастном составе населения. Также нельзя по абсолютному количеством случаев заболеваний с временной потерей трудоспособности судить о здоровье работников промышленных предприятий разной мощности. При сравнении размеров таких явлений, как рождение, смерть, заболевание, травмы, осложнения, или изучении их изменений во времени, нужны абсолютные числа, которые помогают эти явления привести к одному знаменателю, отнести к одному и тому же количеству населения. Абсолютные числа нужны и при распределении общих чисел этих явлений на составные части. Например, в больнице № 1 умерло 20 лиц из 2000 пролеченных больных, а в больнице № 2 за тот же промежуток времени умерло соответственно 30 лиц из 4000 больных. Пытаясь сравнить абсолютное количество умерших (явление), можно сделать ошибочный вывод, будто летальность более высока в больнице № 2, но и количество пролеченных больных (среда) там больше. Если определить количество умерших в каждой из больниц на 100 больных, то окажется, что летальность более высока в больнице № 1 — 1 % против 0,75 % в больнице № 2. Этот пример демонстрирует необходимость расчета относительных величин для характеристики интенсивности распространения явления в среде. Поэтому прибегают к вычислению статистических коэффициентов, виды которых зависят от того, что сопоставляется: явление ли со средой, откуда оно происходит, или составные элементы того же явления, или независимые явления, сравниваемые между собой. Существуют две группы производных величин: относительные — как обобщающая характеристика явления качественным признаком, средние, — обобщающая характеристика по количественному признаку. Интенсивные показатели являются важнейшим видом относительных величин. Среда, в статистическом смысле этого слова, — это основная статистическая совокупность, в которой происходят исследуемые процессы (население определенного города или региона, детский коллектив школы или детсада, коллектив работников предприятия).
Показатели интенсивности разделяют на: • Общие - характеризуют явление в целом относительно всей среды; это общие уровни смертности, рождаемости, заболеваемости, инвалидности и тому подобное; • специальные — по отдельным группами (возраст, пол, причина, стаж работы и тому подобное). Для расчета специальных показателей выбирается часть среды (знаменатель) — показатели плодовитости, повозрастные показатели смертности, — или часть явления (числитель) — заболеваемость населения отдельными болезнями, уровень смертности населения от отдельных причин. Иногда часть явления и среды обосабливаются одновременно (например, коэффициент смертности детей первого года жизни от пневмонии). Относительные величины могут быть выражены в процентах (%), если за основу берется 100, в промилле (°/оо), если за основу берется 1000 и тому подобное.
Размер основы для определения явления выбирают таким образом: чем больше оно распространено, тем меньшая основа. Так общие показатели смертности, рождаемости, заболеваемости, травматизма, инвалидности и тому подобное определяются на 1000 населения; специальные показатели этих явлений часто — на 10 тысяч или 100 тысяч населения; показатели заболеваемости с временной потерей трудоспособности — на 100 работающих, летальности — на 100 больных. Для определения интенсивного показателя нужно брать только ту среду, где имеет место явление, которое изучается. Например, заболеваемость среди всего населения или отдельных его групп, летальность среди всех госпитализированных в больнице или только среди больных, госпитализированных после 24 часов с начала заболевания и тому подобное. Явление и среда должны быть связаны между собой.
Формула расчета общего интенсивного показателя:
Общий уровень(коэффициент)заболеваемости =
Формула расчета специального интенсивного показателя:
Частота распространения гипертонической болезни среди населения:
Основой при расчете частоты или уровня обычно служит численность населения. В других случаях средой могут быть контингенты больных, относительно которых можно получить показатели последствий лечения: выздоровления, летальности, инвалидности. Можно также обнаружить частоту проявлению тех или других симптомов, осложнений, которые сопровождают заболевание. Например, это оперированные больные, относительно которых вычисляют частоту послеоперационных осложнений и летальных последствий. Интенсивные показатели можно сравнивать по времени и в пространстве (в статике и динамике) благодаря приведению их к общему знаменателю (100, 1000, 10000 и тому подобное). Экстенсивными коэффициентами можно характеризовать рождаемость (деление рожденных по полу, росту, весу), смертность и летальность (распределение умерших по возрасту, полу и причинам смерти), заболеваемость (деление больных по нозологическим формам, по срокам госпитализации и тому подобное). С их помощью можно проанализировать состав населения по полу, возрасту, по социальным группами, распределение врачей по специальностям или больничных коек по профилю, распределение инвалидов по причинам и группам инвалидности. В некоторых случаях возможно применение только экстенсивных показателей (формула элементов белой крови, распределение случаев производственного травматизма по причинам и обстоятельствам травм).
Экстенсивный показатель можно определить при наличии общих размеров совокупности и ее составляющих частей. Определение экстенсивного показателя проводится по формуле:
Экстенсивный показатель =
Экстенсивный показатель определяется в процентах. Между интенсивными и экстенсивными величинами существует определенная взаимосвязь и в то же время они являются разными по сути и назначению. Так, например, при изучении структуры заболеваемости может вырасти удельный вес какого-либо отдельного заболевания. Это может состояться в таких случаях: а) при настоящем его росте, то есть при увеличении интенсивного коэффициента; б) при том же уровне — если число других заболеваний в этот период снизилось; в) при снижении уровня данного заболевания, если отмечается уменьшение числа других заболеваний более быстрым темпом.
В тех случаях, когда статистическая природа коэффициентов не полностью понятна, мы рекомендуем помнить о таком критерии: при интенсивных коэффициентах мы всегда имеем дело с двумя четко разграниченными статистическими совокупностями, с двумя самостоятельными, качественно разными совокупностями, одна из которых характеризует среду, а вторая — явление (население и число рожденных, число больных и число умерших). Нельзя считать, что больные «разделились на тех, кто выздоровел, и умерших»: умершие — это другое явление, самостоятельная совокупность. При экстенсивных коэффициентах мы имеем дело лишь с одним статистическим контингентом — только с больными, только с умершими и так далее. Потому, как бы детально не дифференцировался их внутренний состав, информацию о частоте получить нельзя, потому что отсутствуют среда, основа. Это стоит твердо помнить, потому, что наиболее частая ошибка при анализе статистических данных это вывод о частоте на основании данных о распределении. Можно привести пример значительного несоответствия интенсивных и экстенсивных показателей заболеваемости мужчин и женщин (рабочих предприятия).
Заболеваемость работников предприятия.
Экстенсивные коэффициенты дают представления об удельном весе того или другого заболевания (или классе болезней) только в данной группе населения и только за этот год. Поэтому сравнение структурных сдвигов в динамике недопустимо. Следующим видом относительных величин являются показатели соотношения, которые характеризуют численное соотношение двух не связанных непосредственно между собой самостоятельных, разнородных явлений, совокупности или величин (обеспеченность населения койками, врачами, число лабораторных исследований на 100 поликлинических посещений и тому подобное). Эти показатели определяются на 100, 1000, 10000 население. Методика их расчета такая же, как и интенсивных показателей. Отличие заключается в том, что последние характеризуют частоту явления, порожденного данной средой, и с ним связанные. Это не свойственно показателям соотношения.
Пример расчета коэффициента соотношения:
Обеспеченность населения врачебными койками =
Показатели соотношения можно сравнивать между собой в динамике и в пространстве.
Методика расчета показателя соотношения похожа на такую для интенсивных показателей, хотя, в сущности эти показатели разные. Примером расхождений между показателями интенсивности и соотношения могут быть результаты изучения рождаемости и частоты абортов.
Показатель наглядности иногда называют показателем сравнения, поскольку он отображает изменения, которые происходят с тем или другим явлением во времени, показывает их расхождение на отдельных территориях или в разных группах населения. Он показывает, во сколько раз или на сколько процентов изменилось явление в динамике, отличается ли по регионам, не обнаруживая при этом размер последнего.
Для расчета показателя наглядности одна из сравниваемых величин берется за 1, 100 или 1000, а другие рассчитываются по отношении к ней.
При наличии значительных отличий двух сравниваемых величин показатель наглядности лучше отображать в кратности — в сколько раз одна величина больше или меньше другой. Показатели наглядности можно определять, используя абсолютные числа, показатели интенсивности, соотношения или средние величины. Они используются для того, чтобы показать направление, тенденцию изменения явления (увеличение или уменьшение), но не раскрывают, ни абсолютные размеры явления, ни его уровень.
Существует еще одна разновидность относительных величин коэффициент относительной интенсивности, что используется как вспомогательный прием в тех случаях, когда не удаётся получить прямые интенсивные коэффициенты. Коэффициент относительной интенсивности — это числовое соотношение двух структур. Он используется при изучении структурных особенностей разных статистических совокупностей, которые имеют отношение к одной среде, то есть являются численным соотношением двух структур. Коэффициенты относительной интенсивности должны использоваться только в тех случаях, когда нет возможности определить прямые интенсивные коэффициенты.
Например, удельный вес болезней системы кровообращения в структуре первичной заболеваемости составляет 7,4%, в структуре инвалидности 32,4%, в структуре смертности 63,2%. Коэффициенты относительной интенсивности показывают, что болезни системы кровообращения в 9 раз более весомы чем причины смертности и в 4 разы — чем причины инвалидности в сопоставлении с ранговым местом среди причин заболеваемости. При пользовании статистическими коэффициентами могут случаться некоторые ошибки, о которых стоит вспомнить с целью их предотвращения. Самой распространенной среди ошибок является замена интенсивных и экстенсивных коэффициентов в попытке сделать выводы о частоте на основании данных распределения. Нужно помнить, что интенсивные коэффициенты указывают на вероятность данного события в определенной среде, а экстенсивные — на вероятность события или признака лишь по отношению и связью с другими событиями и признаками (так называемая относительная частота). Достаточно типичной ошибкой является попытка сравнить годовой показатель с квартальными или месячными. Так неправомерным является изучение летальности больных в связи с применением новых методов лечения по срокам, которые не совпадают с контрольным периодом применительно к данным методам. При расчете групповых показателей нужно тщательно подбирать среду, то есть выделять определенную её часть, адекватную для данного показателя. Например, летальность от послеоперационных осложнений нельзя вычислять относительно числа всех оперируемых, а только относительно тех из них, кто имел послеоперационные осложнения. Иногда проводят сравнение показателей с разными единицами измерения: показатели частоты заболевания населения, выраженные в %о, сравнивают с заболеваемостью рабочих, которая рассчитывается на 100 работающих.
Табличная сводка статистического материала часто нуждается в наглядном изображении в виде графиков. График, в отличие от таблицы, более наглядно показывает общую картину распределения или тенденцию развития явления. При его использовании прослеживаются более выразительные взаимосвязи между показателями.
Графики используются с целью облегчения восприятия материала, его статистического анализа, сравнения полученных данных. Они помогают лучше понять численные соотношения признаков, закономерности и взаимосвязь отдельных явлений, сделать выводы наглядными. Графические изображения способствуют также популяризации и распространению статистических данных. Только правильно построенный график поможет проиллюстрировать обнаруженную закономерность или тенденцию. Графический образ — это геометрические знаки, линии, фигуры, с помощью которых изображаются статистические данные. Он должен отвечать цели и быть как можно более выразительным. Поле графика — это место размещения графических образов. Пространственные ориентиры — это системы координатных сеток. Часто используют систему прямоугольных координат, кроме того, есть криволинейные шкалы. Они целесообразны в секторных диаграммах. Масштабом графика называется определенная мера перевода количественной величины в графическую. Масштабные ориентиры определяются системой масштабных шкал, которые бывают равномерными и неравномерными. При равномерных масштабных шкалах отрезки пропорциональны числам. Если, например, число удваивается, то отрезок между числами тоже должен быть в два раза большим.
Експликация — это название с коротким изложением содержания, времени и места данных. На диаграмме также должны быть подписи вдоль масштабных шкал, объяснения определённых элементов графика.
Линейные диаграммы (рис. 8) используют для наглядного изображения процессов, которые показывают развитие явления во времени, его динамику, представленную в виде сплошной линии при непрерывности процесса. Явление на такой диаграмме подается в виде линии, которая может быть прямой, ломанной, кривой (температурный листок больного, помесячный вес ребенка, заболеваемость, в зависимости от возраста и др.).
При построении линейной диаграммы осью абсцисс является горизонтальная линия (ось X). На ней откладывают отрезки для воспроизводимых групп (например, количество лет, за которые сравнивают данные). Они должны быть равные и непрерывные. Если статистические данные охватывают разные периоды времени, интервалы между периодами (длина отрезка) на абсциссе должны быть пропорциональные величинам продолжительности периодов. На вертикальной линии (осьY), ординате, наносят отметки, каждая из которых отвечает определенному количественному значению явления. Подсчет по масштабной линии проводится от базисной линии. После того, как на оси абсцисс и ординат нанесена шкала по определённому масштабу в соответствии с приведенными данными, обозначают точки (координаты) на поле диаграммы, которые образуются пересечением двух прямых, проведенных перпендикулярно к соответствующим точкам на осях координат. Точки соединяются линиями. Радиальной диаграммой можно изобразить, например, частоту вызовов скорой помощи к детям при заболеваниях пневмонией по месяцам года (рис. 9). Для построения такой диаграммы нужно иметь соответствующее распределение вызовов. Радиусом произвольной длины описывают круг. Шестью диаметрами делят его на ровные отрезки. Дальше определяем:
1) среднее число вызовов в день за каждый месяц; 2) среднее число вызовов в день за год; 3) для каждого месяца определяем относительный показатель в процентах:
На сделанных таким образом двенадцати радиусах (по числу месяцев), или их продолжениях, откладываем значения рассчитанного показателя пропорционально принятому масштабу. За масштаб принимается величина радиуса, который отвечает среднесуточному числу вызовов за год. Рассчитанные значения откладывают на принятой длине радиуса, и отмеченные точки соединяют линиями. Полученный многоугольник отображает колебание вызовов по месяцам. Среди плоскостных диаграмм самыми распространенными являются столбиковые, внутристолбиковые и секторные. При построении столбиковой диаграммы необходимо начертить систему прямоугольных координат, обозначить размеры каждого столбика и интервалы между ними. Основа столбиков, которая должна быть одинакового размера, размещается на оси абсцисс, а верхняя его часть будет соответствовать величине показателя, который нанесен в соответствующем масштабе относительно оси ординат.
Каждый отдельный столбик отвечает отдельному явлению или одному явлению за разные периоды времени. Расстояние между столбиками должно быть одинаковым, однако иногда они размещаются друг около друга. Пример столбиковой диаграммы приведен на рис. 10.
Рис. 10. Сравнительная характеристика демографических показателей городского и сельского населения Украины за 1990-2007 гг.
Столбиковые диаграммы используются не только для сравнения явления в динамике, но и для демонстрации состава определенного явления (внутристолбиковые диаграммы).
Составляющие части явления подаются в виде процентов к общему числу (рис. 11).
Рис. 11. Структура госпитализированных больных по классам болезней в Украине, в 2005 г.
При этом высота столбика берется за 100% и делится на части пропорционально удельному весу отдельных частей в процентах. Их размещают в порядке снижения (роста) процентов.
Для построения секторной диаграммы радиусом произвольной величины описывают круг. На нём откладывают в градусах части круга, пропорциональные процентному распределению изображенных данных, которые определяют по формуле: X = 360: 100 • а = 3,6 • а, где X — число градусов, а — число процентов. Размеченные отрезки круга соединяют линиями с центром, образовывая секторы, размер которых наглядно демонстрирует структуру явления. Для большей наглядности используют объемные диаграммы, представляя данные в виде геометрических фигур, рисунков, символов. Например, фигуры людей, рисунок кровати, — для изображения числа больных, коек и др.
Структуру наблюдаемого явления (заболеваемости, смертности и др.) можно подать также в виде секторной диаграммы (рис. 12). Картограммы и картодиаграммы дают представление о территориальной распространенности определенного явления в абсолютных или относительных величинах, которые размещают на географических картах. Картограммы — способ наглядного изображения практических показателей, которые характеризуют отдельные географические единицы (районы, области, государства) по тому или другому признаку. Для этого на географическую карту наносят штрихованием или цветом разных оттенков разную интенсивность и распространенность явления. Если принять для каждой группы районов определенный способ штриховки, то будет хорошо видно, как расположены на территории области разные районы по распространенности заболеваний или других явлений (рис. 13). Условные обозначения по качественной шкале оценивания уровней показателей (комплексное оценивание по Полякову - Малинскому).
Недостатком таких картограмм является то, что они дают только общее представление об отличиях статистических показателей в районах, но не показывают их абсолютных значений. Картодиаграмма отличается от картограммы тем, что на географическую карту определенной территории наносят в небольшом масштабе линейные, столбиковые диаграммы, которые могут отображать абсолютные или относительные числа. Это позволяет определить колебание показателей в регионах. При этом соответствующим цветом фона самой территории могут быть изображены другие показатели.
Вопросы для обсуждения: 1. Какие значения имеют абсолютные величины, в каких случаях они используются? 2. Какие ошибки чаще всего случаются при нахождении и анализе относительных величин? 3. Какие относительные величины можно использовать для сравнения явлений, которые изучают в динамике, по территориям, в отдельных группах? 4. С какой целью используют графики? 5. Какие основные элементы графика? 6. Какие величины используют для построения графических изображений?
|



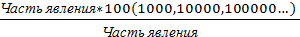



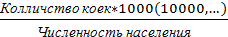
 0
Интенсивный показатель частоты абортов составляет:
0
Интенсивный показатель частоты абортов составляет:  = 86,6%0
Коэффициент соотношения равен:
= 86,6%0
Коэффициент соотношения равен:  , то есть на 100 родов припадает 216 абортов.
Из приведенного примера видно. Что показатели здоровья выражается преимущественно интенсивными коэффициентами. Потому что население представляет собой среду, в которой происходят процессы, определяющие здоровье.
, то есть на 100 родов припадает 216 абортов.
Из приведенного примера видно. Что показатели здоровья выражается преимущественно интенсивными коэффициентами. Потому что население представляет собой среду, в которой происходят процессы, определяющие здоровье.
 В нашем примере базовая величина, с которой другая составляется, равна 8%0. Для того чтоб сделать вывод, необходимо от определенной величины отнять 100%.
Вывод: уровень рождаемости а районе увеличился на 12,5%.
В нашем примере базовая величина, с которой другая составляется, равна 8%0. Для того чтоб сделать вывод, необходимо от определенной величины отнять 100%.
Вывод: уровень рождаемости а районе увеличился на 12,5%.










