Год 2000-й Апрельский день Часть первая. Construction is growing from year to year in our great country
Construction is growing from year to year in our great country. Millions of people get new flats and houses built by modern methods and materials. How are the houses built? What are the main strategies in building operations? The first step in any building is the designing and complete planning of all the operations. If a house is to be built architects and designers draw the plans and define the size of the walls, floor joists, beams, girders and other parts which make up the framework. All the parts of the building should be correctly designed and well proportioned. Building operations on the site begin with the clearing and grading the site area. This work is done by the bulldozers and scrapers. The traditional way of building a house is to dig an excavation for the basement. Earth moving is carried out by excavators. After this foundations are built. Foundations carry the weight of the building and transfer it to the basement. Foundation walls are constructed below the ground level. They may be constructed of brick, stone or concrete panels and slabs. The part upon which the stability of the structure depends is the framework. Its ability is to carry the loads which will be imposed upon it. The framework is raised upon the foundation and infilled with brickwork, window-frames, panels and so on. Walls are constructed to enclose areas and to support the weight of floors and the roof. Exterior walls are usually made of brick, stone, concrete blocks or large panels. In the case of a brick structure raising the walls follows directly the foundation work. Making brick walls, bricklayers lay down courses of brick and bond them together with mortar. The instruments used by bricklayers are a trowel, a brick chisel and a hammer. For windows and doors openings are left in the walls. Window-frames and door-frames are placed in position but later. Walls and partitions are made to divide the floor space into rooms. Floors divided the building into stories. Stairs are provided for going up and down. The whole structure is covered by the roof. Today most of the blocks of the flats are assembled on the site from prefabricated units. All the units for houses are manufactured at house building plants and delivered to the construction site by powerful lorries and trailers. Efficient cranes pick up the prefab units from the lorries and install them into position. Erection is simple. A team of assembly workers of 709 men complete erection in a short time. Nowadays a lorry brings to the site a complete flat with interior decoration. A powerful gantry crane lifts the 29ton flat, carefully sets it on the foundation. The electricians, plumbers and gas men begin their work on the installation service.
Answer the following questions: 1. What is the first step in any building? 2. What work is done by architects and designers? 3. Should all the parts of the building be correctly designed? 4. How do building operations begin on the site? 5. What work is done by bulldozers and scrapers? 6. What work is carried out by excavators? 7. What is the function of the foundations? 8. What materials are foundation walls made of? 9. What does the stability of the structure depend on? 10. What is its ability? 11. What is the framework infilled with? 12. For what are walls constructed? 13. What materials are exterior walls made of? 14. What specialists lay down courses of brick? 15. What instruments do they use? 16. What is the function of partitions, floors and stairs? 17. What is the crowning part of a house? 18. What units are block flats assembled from? 19. Where are the units for houses manufactured? 20. How are they delivered to the site? 21. How are they hoisted into position? 22. What specialists carry out erection? 23. Whom is the installation of services done by?
ВЫСШАЯ МАТЕМАТИКА Контрольная работа №2 Для экономических специальностей заочной формы обучения Вариант A Задание 1. Вычислить неопределенные интегралы:
Решение. а) При вычислении данного интеграла, сделаем подстановку t =5–9ln x, в результате получим
б) При вычислении данного интеграла, сделаем подстановку t =5+4 x 10, в результате получим
в) При вычислении данного интеграла воспользуемся формулой интегрирования по частям
Тогда получим
г) При вычислении данного интеграла также воспользуемся формулой интегрирования по частям. В результате получим
д) Разложим подынтегральную функцию, т.е. правильную рациональную дробь, на сумму простейших дробей:
Приведем правую часть равенства к общему знаменателю и приравняем числители левой и правой частей:
Чтобы найти неопределенные коэффициенты A, B, C, придадим переменной x три каких-либо значения (обычно выбирают такие значения, чтобы получались нулевые значения в правой части):
Таким образом,
Далее, вычисляем исходный интеграл
е) Для вычисления исходного интеграла применим тригонометрические формулы:
Тогда получим
Задание 2. Вычислить определенные интегралы:
Решение. а) При вычислении данного интеграла, преобразуем подынтегральное выражение
б) При вычислении данного интеграла применим метод замены переменной (обратим внимание, что в определенных интегралах, кроме подынтегрального выражения, преобразуются также и пределы интегрирования):
в) При вычислении данного интеграла применим метод интегрирования по частям:
Задание 3. а) В урне содержатся 3 синих, 5 красных и 2 белых шара. Из нее наудачу извлекаются сразу два шара. Найти вероятность того, что будут вынуты либо два белых шара, либо два разных цветных шара. б) Наудачу взятый телефонный номер состоит из 5 цифр. Какова вероятность, что в нем все цифры разные? Решение. Вспомним классическое определение вероятности: вероятностью события А называется отношение числа m благоприятствующих этому событию исходов к общему числу n всех равновозможныхнесовместных элементарных исходов, образующих полнуюгруппу:
Вероятность P (A) события А должна удовлетворять следующим условиям: 1о. P (A)=1, если А – достоверное событие; 2о. P (A)=0, если А – невозможное событие; 3о. 0< P (A)<1, если А – случайное событие. Для подсчета вероятностей по классической формуле обычно используют методы комбинаторики. Комбинаторика – это раздел математики, посвященный решению задач выбора и расположения элементов в соответствии с каким-либо правилом. Существует две принципиально различные схемы выбора. В первой схеме выбор осуществляется без возвращения элементов. Это означает, что в выборке невозможны повторения элементов. Во второй схеме выбор осуществляется по-элементно с обязательным возвращением отобранного элемента при каждом шаге. Это означает, что в выборке возможны повторения. После того, как выбор тем или иным способом осуществлен, отобранные элементы могут быть либо упорядочены, либо неупорядочены. В первом случае, выборки, состоящие из одних и тех же элементов, но отличающиеся порядком следования этих элементов, объявляются различными. Во втором случае порядок следования элементов не принимается во внимание, и такие выборки объявляются тождественными.
а) Поскольку в данной задаче неважен порядок, то для решения будем применять сочетания без повторения (шары не возвращаются обратно в урну). Найдем общее число возможных исходов:
Теперь найдем число благоприятствующих возможных исходов. Два белых шара можно вынуть m 1= C 22=1 способом, два разных цветных шара m 2= C 31× C 51=3×5=15 способами. Тогда общее число благоприятствующих исходов, в соответствии с принципом сложения, равно m = m 1+ m 2 = 16. Таким образом,
б) Всего имеется 10 цифр. Поскольку при составлении пятизначным номеров важен порядок и возможны повторения, то общее число возможных пятизначных номеров будет равно
Номера, у которых все цифры разные, – это размещения без повторений
Таким образом, искомая вероятность равна
Задание 4. а) В урне содержатся 3 синих, 5 красных и 2 белых шара. Из нее наудачу извлекаются сразу два шара. Найти вероятность того, что будут вынуты либо два белых шара, либо два разных цветных шара. б) Наудачу взятый телефонный номер состоит из 5 цифр. Какова вероятность, что в нем все цифры разные? Решение. Вспомним теоремы сложения и умножения вероятностей: Теорема сложения вероятностей несовместных событий. P (A+B) = P (A) + P (B). Теорема сложения вероятностей совместных событий. P (A+B) = P (A)+ P (B)– P (AB). Теорема умножения вероятностей независимых событий. P (AB) = P (A) P (B). Теорема умножения вероятностей зависимых событий. P (AB) = P (A) PA (B) = P (B) PB (A). Достоверное событием обычно обозначается символом W, невозможное событие – символом Æ. Тогда
а) Пусть событие В состоит в том, что выстрел произошел, тогда событие P (AB) = P (B) PB (A) = 0б98×0б8 = 0б784. б) Пусть A 1={первый стрелок попал по цели}, A 2={второй стрелок попал по цели}. Мишень будет поражена (событие В), если произойдет событие А 1+ А 2. Поскольку события А 1 и А 2 совместны, но независимы, то P(А 1+ А 2) = P (А 1)+ P (А 2)– P (А 1) P (А 2) = 0,7+0,8–0,7×0,8 = 0,94. Отметим, что событие В можно записать также в виде P (B) = P (A 1) P ( Задание 5. а) Вероятность изготовления на станке-автомате нестандартной детали равна 0,02. Какова вероятность того, что среди наудачу взятых шести деталей окажется более четырех стандартных? б) Вероятность того, что сошедшая с конвейера деталь стандартная равна 0,9. Найти вероятность того, что из 400 сошедших с конвейера деталей: 1) 356 окажутся стандартными; 2) более 350 деталей окажутся стандартными. Решение. а) Проведем n испытаний Бернулли, т.е. что все n испытаний независимы и вероятность появления события А в каждом отдельном взятом испытании постоянна и от испытания к испытанию не изменяется (т.е. испытания проводятся в одинаковых условиях). Обозначим вероятность P (A) появлений события А в отдельном испытании буквой p, т.е. P (A)= p, а вероятность противоположного события P (
Это есть формула Бернулли. По условию задачи, вероятность того, что наудачу взятое изделие окажется нестандартным равна q =0,02. Вероятность того, что изделие окажется стандартным равна p= 1– q =0,98. Поскольку эти вероятности постоянны и не изменяются от испытания к испытанию, то для подсчета вероятности можно применить формулу Бернулли. Появление более четырех стандартных изделий означает, что среди 6 взятых деталей окажутся 5 или 6 стандартных. Следовательно
= 5×0,985×0,021 + 1×0,986×0,020» 0,9943. б) Применим к случаю 1 локальную теорему Муавра-Лапласа: если в схеме Бернулли число испытаний n велико (обычно nt50), при этом npq ‡1, то справедлива приближенная формула
где Ввиду важности функции j(x), которая называется плотностью стандартного нормального распределения, для нее составлены специальные таблицы. При использовании таблиц следует учитывать, что функция j(x) четная, т.е. j(– x)=j(x). Согласно условию задачи: n =400, m =356, p =0,9, q =0,1. Поскольку n >100 и npq =36>10, то можно применить теорему Муавра-Лапласа. Найдем
После этого находим значение функции j(–0,6667)=0,31945. В результате, получаем
Применим теперь к случаю 2 интегральную теорему Муавра-Лапласа: если в схеме Бернулли число испытаний n велико, то для вероятности P n (k 1£ m £ k 2) того, что число успехов заключено в пределах от k 1 до k 2, справедливо приближенная формула
где Отметим, что функция Лапласа – нечетная функция, т.е. Ф(– x) = –Ф(x), для которой составлены специальные таблицы. Обратите внимание, что 0£Ф(x)£0,5. В нашем случае k 1=300, k 2=400:
Задание 6. Дискретная случайная величина Х имеет только два возможных значения: x 1 и x 2, причем x 1 < x 2. Вероятность того, что Х примет значение x 1 равно 0,6. Найти закон распределения Х, зная математическое ожидание М[ X ] = 1,4 и дисперсию D[ X ] = 0,24. Решение. Сумма вероятностей всех возможных значений X равна единице, поэтому вероятность того p 2, что X примет значение x 2, равна 1–0,6=0,4. Запишем закон распределения дискретной случайной величины X:
Для отыскания x 1 и x 2 составим два уравнения. По определению M[ X ] = Учитывая, что по условию М[ X ] = 1,4, запишем первое из уравнений:
Принимая во внимание, что по условию D[ X ] = 0,24, и используя равенство
напишем второе уравнение:
В результате получается следующая система уравнений:
Выразив x 1 из первого уравнения и подставив его во второе, получим квадратное уравнение
Отсюда находим два решения:
Задание 7. Непрерывная случайная величина Х задана функцией распределения.
Решение. Найдем плотность распределения f (x)= F' (x):
Параметр k определим из условия
В нашем случае
Таким образом, плотность распределения имеет вид
Найдем теперь математическое ожидание
Найдем теперь дисперсию, для этого предварительно вычислим
Тогда
Задание 8. Известны математическое ожидание а =165 и среднее квадратичное отклонение s=5 нормально распределенной случайной величины Х. Найти вероятность: а) попадания этой величины в заданный интервал Решение. Плотность функции нормального распределения имеет вид:
Функция нормального распределения имеет вид
Однако часто вместо функции нормального распределения используется функция Лапласа F(x):
где а) Вероятность того случайная величина X, описываемая нормальным распределением, примет значение, принадлежащее интервалу (a,b), имеет вид
В нашем случае получим
б) Вероятность того, что отклонение случайной величины X от математического ожидания по абсолютной величине меньше заданного положительного числа d, вычисляется по формуле:
В нашем случае получим
ТАБЛИЦА ПРОСТЕЙШИХ ИНТЕГРАЛОВ
Год 2000-й Апрельский день Часть первая 1 Сон теперь бежал его чаще — не единожды-дважды в неделю, а раза четыре, пять. Что он делал тогда? Долгих прогулок в развертке зари не предпринимал. Излюбленного друга, чтобы терзать звонками, у него нет. Да и что скажешь? Тут в молчании суть, не в словах. Пытался убаюкивать себя чтением, но лишь просыпался больше. Читал науку и стихи. Ему нравилась скудная поэзия, точно размещенная в белом пространстве, шеренги штрихов, выстроенные по ранжиру алфавита, выжженные на бумаге. От поэзии он сознавал свое дыхание. Стихотворение обнажает миг для того, что обычно не готов замечать. Таков оттенок каждого стихотворения — по крайней мере, для него по ночам, все эти долгие недели, один вдох за другим, в комнате, что вращалась на верхушке трехэтажной квартиры. Как-то ночью попробовал спать стоя в отсеке для медитаций, однако не обнаружилось в нем должного послушничества, не монах. Он превозмог сон и постепенно уравновесил его — в безлунном спокойствии, где всякая сила уравновешена другой. Кратчайшее облегчение, крохотная пауза в возне неуемных личностей. На вопрос ответа не было. Он пробовал успокоительные и гипноз, но те его подсаживали, отправляли вовнутрь по тугим спиралям. Что ни действие, то призрак себя, неестественное. За самой блеклой мыслью тащилась суетливая тень. Что же он делал? К аналитику в высокое кожаное кресло не садился. С Фрейдом покончено, следом пойдет Эйнштейн. Ночью читал «Специальную теорию относительности» — по-английски и по-немецки, — но в итоге книгу отложил, а сам лег совсем неподвижно, стараясь собраться с силами и выговорить то единственное слово, от которого свет погаснет. Вокруг ничего нет. Только шум в голове, рассудок во времени. Когда умрет, он ведь не кончится. Кончится мир вокруг.
Он стоял у окна и рассматривал грандиозную дневную зарю. Вид открывался на мосты, протоки и проливы, за ними дальние районы и умывальные пригороды, а дальше — толики суши и неба, которые иначе как глубокой далью и не назвать. Он не знал, чего ему хочется. На реке еще лежала тьма, полуночь, а над дымовыми трубами на другом берегу подрагивали пары пепла. Он представлял себе, что все шлюхи уже разбежались из-под фонарей на перекрестках, потряхивая утиными попками, а прочая деловая архаика только начинает копошиться, с рынков выезжают фуры с провизией, из экспедиций — фуры с газетами. По городу снуют хлебные фургоны да тачки из бедлама, отбившиеся от стай, выписывают зигзаги по проспектам, а из динамиков несется тяжкий грохот. Зрелище благороднее некуда — мост через реку, за ним уже принимается реветь солнце. Он смотрел, как сотня чаек не отстает от качкой баржи, идущей вниз по реке. Мощные у них сердца, крупные. Он знал это: непропорционально размерам тела. Некогда его интересовала анатомия птиц, и он освоил ее несметные подробности. У птиц полые кости. Невероятно, сколько всего он тогда выучил за полдня. Поди пойми, чего ему хочется. И тут понял. Ему хочется подстричься. Он еще немного постоял, глядя, как в свитке воздуха взмывает и трепещет одинокая чайка, повосхищался птицей, повдумывался в нее, стараясь ее познать и ощущая всем собой крепкое искреннее биенье алчного сердца помойной твари.
Надел костюм и галстук. Костюм скрадывал выпуклость перекачанной груди. Разминаться ему нравилось по ночам — тягать металлические штанги по салазкам, гнуться и качать пресс, стоически повторяя одно и то же, от чего съедались все дневные дрязги и натиски. Прошел по квартире — сорок восемь комнат. Он так делал, если сомневался и унывал, — шагал мимо бассейна с дорожками, карточного салона, спортзала, мимо аквариума с акулой и кинозала. Остановился у загона с борзыми, поговорил с собаками. Потом зашел в пристройку, где отслеживались валюты и просматривались исследовательские отчеты. Курс иены за ночь поднялся, против ожиданий. Он вернулся в жилые апартаменты — уже медленно, задерживаясь в каждой комнате, впитывая все, что там есть, прозревая глубь, ухватывая всякую крупицу энергии, лучами и волнами. Живопись — почти сплошь цветовые поля и геометрия, огромные холсты господствовали в комнатах, а в атрии, с его световым куполом, высокими белыми полотнами и фонтанной струйкой, нагнетали молитвенную тишь. В атрии висели напряжение и тревога — такая громоздящаяся пустота требует почтительной тишины, лишь в ней это пространство можно рассмотреть и прочувствовать как полагается, это мечеть тихих шагов и сизарей, что курлычут под сводами. Ему нравились такие картины, на которые гости не знали, как смотреть. Белые полотна многим были неизвестны — мазки тонированной слизи наносились мастихином. Работа еще опаснее оттого, что не нова. В новом никакой опасности уже нет.
На лифте, где играл Сати,[2] он спустился в вестибюль. У него асимметричная простата. Вышел наружу и пересек авеню, обернулся и посмотрел на дом, в котором живет.[3] Он чувствовал себя смежным. В доме восемьдесят девять этажей, простое число в неприметном футляре дымчатого бронзоватого стекла. У них с домом общий край или граница — небоскреб и человек. Высота — девятьсот футов, высочайшее жилое здание на свете, банальный параллелепипед, примечательный лишь размером. В нем та пошлость, чья взаправдашняя грубость проявляется лишь со временем. Потому дом ему и нравился. Он любил стоять и смотреть на дом, когда ему бывало так же, как сейчас. А ему настороженно, сонно и незначительно. От реки подуло вприпрыжку. Он вынул ручной органайзер и набил себе заметку об анахронизме самого слова «небоскреб». Ни одна из нынешних конструкций не должна носить такого имени. Оно целиком принадлежит былой душе, исполненной благоговения, тем стрельчатым башням, что были повествованием задолго до того, как он родился. Сам ручной приборчик — объект, чья первоначальная культура уже почти исчезла. Надо выбросить, это он точно знал. Башня внушила ему силу и глубину. Он знал, чего хочет — подстричься, — но еще немного постоял в воспаряющем уличном шуме, поизучал масштабы и массу башни. У ее поверхности одно достоинство — она бегло просматривает и преломляет свет реки и передразнивает приливы и отливы распахнутого неба. В ней чудятся характер и рефлексия. Он пробежал взглядом всю ее длину и ощутил связь с башней — они с ней делили одну поверхность и среду, которая вступала с этой поверхностью в контакт, причем с обеих сторон. Поверхность отъединяет то, что внутри, от того, что снаружи, а сама одному принадлежит не больше, чем другому. Он думал о поверхностях как-то раз в душе.
Надел темные очки. Затем перешел через дорогу обратно, к рядам белых лимузинов. Всего десять машин — пять у обочины Первой авеню прямо перед домом, еще пять на боковой улице, смотрят на запад. С первого взгляда все одинаковые. Ну, может, некоторые на фут-другой длиннее — все зависит от деталей растяжки и особых требований владельца. Шоферы курили и общались на тротуаре — простоволосые, в темных костюмах, все бдительные, но это заметно лишь потом, когда у них вспыхивают глаза, они отбрасывают окурки и непринужденные позы, засекши объекты своего внимания. Пока же они беседовали, некоторые с акцентами, другие на родных языках, — поджидая каждый своего инвестиционного банкира, застройщика, венчурного капиталиста, производителя ПО, владельца глобальных спутниковых и кабельных сетей, дисконтного брокера, клювастого медиамагната, главу государства в изгнании, сбежавшего из сокрушенного пейзажа глада и войны. В скверике через дорогу стояли стилизованные железные деревца и бронзовые фонтаны, на дне всеми цветами радуги переливались разбросанные монетки. Мужчина в женской одежде выгуливал семерку элегантных собак. Ему нравилось, что машины практически неотличимы друг от друга. Самому хотелось такой автомобиль, поскольку это платоническая копия, несмотря на размер, не обладающая собственной плотностью, скорее идея, нежели объект. Но он знал, что это не так. Такое он говорил, исключительно чтобы произвести впечатление, сам же не верил ни секунды. Секунду, то есть, верил, но едва-едва. Ему хотелось машину не только потому, что она чрезмерного размера, но потому, что она чрезмерна агрессивно, презрительно, метастатически — неохватный мутант, встающий на пути у любых доводов против себя. Его начальник службы безопасности любил эту машину за ее обезличенность. Длинные белые лимузины давно стали самым незаметным транспортным средством в городе. Он теперь ждал на тротуаре — Торваль, лысый, шеи нет, казалось, голова у него отвинчивается на техобслуживание. — Куда? — спросил он. — Хочу подстричься. — В городе президент. — Нам до лампочки. Нам нужно подстричься. Нам надо на другой конец города. — Пробки будут разговаривать с вами четверть-дюймами. — Известное дело. О каком президенте речь? — Соединенных Штатов. Все перегородят, — сообщил он. — Целые улицы сотрут с карты. — Покажи мою машину, — сказал он начальнику. Шофер придержал дверцу, изготовясь обежать машину сзади к своей двери, что в тридцати пяти футах. Где заканчивался ряд белых лимузинов — параллельно входу в Японское общество,[4] — начинался другой: городских легковых, черных или сине-фиолетовых, и шоферы там ждали работников дипломатических миссий, делегатов, консулов и атташе в темных очках. Торваль сел к шоферу впереди, где в приборную доску встроены компьютерные экраны, а внизу ветрового стекла — монитор ночного видения, производное инфракрасной камеры, вмонтированной в решетку радиатора. В машине его ждал Шайнер — руководитель отдела технологических разработок, мелкий, с мальчишеским лицом. На Шайнера он больше не смотрел. Уже три года. Только посмотришь — и все ясно. Виден костный мозг в мензурке. На нем была линялая рубашка и джинсы, а сидел он, мастурбационно скрючившись. — Так что мы узнали? — Наша система надежна. Мы неприступны. Никаких вредоносных программ, — ответил Шайнер. — И тем не менее. — Эрик, нет. Мы все тесты прогнали. Никто систему не завешивает, нашими сайтами не манипулирует. — И когда мы все это сделали? — Вчера. В комплексе. Наша команда быстрого реагирования. Уязвимой точки входа нет. Наш страховщик провел анализ угроз. У нас буфер против атак. — Повсюду. — Да. — Включая машину. — Включая, абсолютно, да. — Мою машину. Эту машину. — Эрик, да, прошу тебя. — Мы с тобой вместе со времен того паршивенького стартапа. Скажи мне еще раз, что тебе по-прежнему хватает выдержки на эту работу. Преданности. — Эта машина. Твоя машина. — Непреклонной воли. Потому что мне все время рассказывают про нашу легенду. Мы все молоды, умны, и воспитали нас волки. Однако репутация — явление нежное. Человек взлетает словом и падает слогом. Я знаю, что не у того спрашиваю. — Что? — Где вчера вечером была машина после того, как мы прогнали тесты? — Не знаю. — Куда по ночам вообще ездят все эти лимузины? Шайнер уныло просел в глубины вопроса. — Я знаю, что меняю тему. Мало сплю. Смотрю на книги и пью бренди. Но что происходит с вытянутыми лимузинами, которые целыми днями рыщут по неугомонному городу? Где они ночуют?
Машина застряла в пробке, не доехав до Второй авеню. Он сидел в клубном кресле в заднем конце салона, смотрел на батарею видеотерминальных устройств. На каждом экране — попурри данных, текучие знаки и хребты графиков, пульсируют многоцветные числа. Он впитывал материал пару долгих недвижных секунд, не обращая внимания на звуки речи, издававшиеся лакированными головами. Еще микроволновка и кардиомонитор. Он взглянул на скрытую камеру на вертлюге, и она глянула на него. Бывало, он держал это пространство руками, но теперь всё. Контекст почти бесконтактный. По слову его большинство систем включается, от одного взмаха руки пустеют мониторы. Сбоку втиснулось такси, водитель жал на клаксон. Это разбудило сотню других клаксонов. Шайнер поерзал на откидном сиденье у встроенного бара, лицом назад. Он цедил свежевыжатый апельсиновый сок через пластиковую соломинку, торчавшую из стакана под тупым углом. Между приемами жидкости он, похоже, что-то насвистывал в стебель соломинки. Эрик спросил: — Что? Шайнер поднял голову. — У тебя бывает иногда чувство, когда ты не знаешь, что происходит? — спросил он. — Мне переспрашивать, что ты имеешь в виду? Шайнер говорил в соломинку, словно она бортовое передающее устройство. — Весь этот оптимизм, весь расцвет и парение. Все бац — и происходит. Одновременно то и это. Протягиваю руку — и что я чувствую? Я знаю, что каждые десять минут ты анализируешь тысячи разных вещей. Паттерны, коэффициенты, индексы, целые поля информации. Я обожаю информацию. Она у нас сладость и свет.[5] Такое чудо, что ебтвоюмать. И для нас в мире есть смысл. Люди едят и спят под сенью того, что мы делаем. Но в то же время — что? Повисла долгая пауза. Наконец он посмотрел на Шайнера. Что он ему сказал? Реплика не прозвучала направленно: остро и резко. Вообще-то ничего он и не сказал. Они сидели в прибое клаксонов. Шум звучал так, что Эрику не хотелось его отменить. Тональность какой-то подлежащей боли, причитания столь древнего, что казалось первобытным. Ему представились оборванные шайки мужчин — церемонно ревут, ячейки общества учреждены ради убийства и поедания. Сырое мясо. Вот к чему этот зов, эта тяжкая нужда. Сегодня в кулере ехали напитки. Для микроволновки — ничего существенного. Шайнер спросил: — А мы по особому поводу в машине, а не в конторе? — Откуда ты знаешь, что мы в машине, а не в конторе? — Если я отвечу. — На основании какого допущения? — Я знаю, что
|




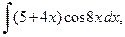


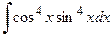 .
.

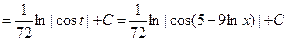 .
.
 .
. .
.
 .
.
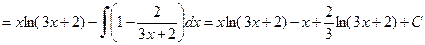 .
. .
.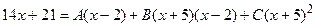 .
.
 .
.
 .
.
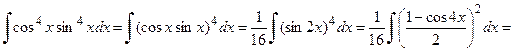

 .
.

 .
.

 .
.
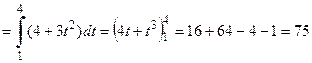 .
.

 .
.
 Набор
Выбор
Набор
Выбор






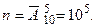


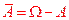
 означает противоположное событие, т.е. что произошла осечка. По условию P (
означает противоположное событие, т.е. что произошла осечка. По условию P ( . Тогда получим
. Тогда получим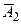 )+P(
)+P( )P(A 2)+ P (A 1) P (A 2) == 0,8×0,3+0,2×0,7+0,7×0,8 = 0,94.
)P(A 2)+ P (A 1) P (A 2) == 0,8×0,3+0,2×0,7+0,7×0,8 = 0,94. ) – буквой q, т.е. P (
) – буквой q, т.е. P ( .
.
 ,
,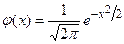 ,
,  .
. .
. .
. ,
, ,
,  – функция Лапласа.
– функция Лапласа.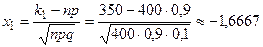 ,
,  ,
,
 = x 1 p 1+ x 2 p 2+... + xnpn.
= x 1 p 1+ x 2 p 2+... + xnpn. .
. ,
, , или
, или  .
.
 .
. и
и  (отсюда получаем также, что
(отсюда получаем также, что  и
и  ). По условию
). По условию  , поэтому задаче удовлетворяет только первое решение. Таким образом, искомый закон распределения имеет вид
, поэтому задаче удовлетворяет только первое решение. Таким образом, искомый закон распределения имеет вид

 .
. .
.

 .
.
 .
. .
. .
.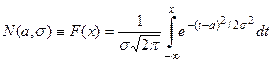 .
. ,
, – функция Лапласа.
– функция Лапласа.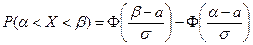 .
.
 .
.

 ,
,
 ,
,
 , a ¹1,
, a ¹1,
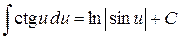 ,
,
 ,
,
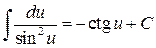 ,
,
 ,
,
 ,
,
 ,
,
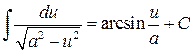 ,
,
 ,
,
 ,
,
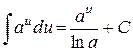 ,
,
 ,
,
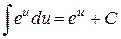 ,
,
 ,
,
 ,
,
 ,
,
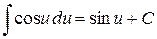 ,
,
 .
.



