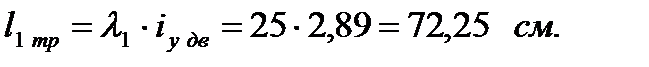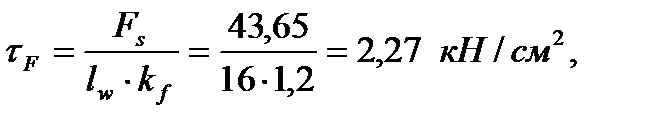Конструирование и расчет стержня сквозной колонны
Расчетная схема колонны проведена на рисунке 3.1. Определяем фактическую длину колонны, учитывая, что база заглублена ниже отметки уровня пола на 600...800 мм (рисунок 3.1): а) при поэтажной схеме сопряжения балок:
где Hвн – отметка верха настила; hбн = 270 мм – высота балки настила из примера 1; tн = 8 мм – толщина настила из примера 1; h = 1460 мм – высота главной балки из примера 2; a = 30 мм – выступающая часть опорного ребра главной балки из примера 2.
Расчетная длина колонны в обеих плоскостях при шарнирномопирании стержня в верхнем и опорном узлах равна:
Расчетная нагрузка на колонну:
где qp – расчетная нагрузка на главную балку из примера 2 (кН/м); 1,01 – коэффициент, учитывающий собственный вес колонны; l – пролет главной балки.
Задаемся гибкостью стержня колонны
Принимаем сечение из двух двутавров №36 (рисунок 4.1). Геометрические характеристики сечения двутавра: Aдв= 61,9 см2, Jxдв = 13380 см4, ixдв= 14,7см, Jyдв= 516 см4, iyдв = 2,89 см. Проверяем сечение относительно материальной оси (ось Х). Гибкость колонны:
По таблице 72 [1] jх = 0,763. Устойчивость колонны относительно материальной оси:
Недонапряжение составляет:
Поэтому оставляем сечение из двух двутавров №36. Из условия равноустойчивости колонны относительно обеих осей (Х и У) принимаем lх = lef. Для двухветвевых стержней необходимо учитывать повышенную гибкость относительно свободной оси (ось У) за счет деформативности решетки. Задаемся гибкостью ветви l1 = 25 (рекомендуется 20…40) и определяем требуемую гибкость относительно оси У:
после чего вычисляем требуемый радиус инерции:
По таблице 3.1 определяем коэффициент ay = 0,52 и вычисляем требуемую ширину сечения:
Принимаем b = 32 см. Зазор b1 между полками двутавров не должен быть менее 15,0 см из условия окраски внутренних поверхностей колонны. Проверяем условие:
где bп = 14,5 см – ширина полки двутавра №36. Проверяем сечение относительно оси Y. Требуемая длина ветви (расстояние между планками):
Принимаем окончательно длину ветви l 1 = 75 см. Уточняем ее гибкость:
Задаемся сечением планки: hs= 0,5×b = 0,5×32 = 16см (рекомендуется hs = 0,5b...0,75b); ts = 10 мм (рекомендуется (1/10...1/25)×hs или 6...10 мм). Момент инерции планки:
Длину планки принимаем на 8…12 см больше величины зазора:
Определяем момент инерции сечения колонны относительно оси Y:
Определяем соотношение погонной жесткости планки к погонной жесткости ветви:
В соответствии с таблицей 7 [1] при таком соотношении приведенная гибкость определяется по формуле:
где ly – гибкость стержня относительно свободной оси:
n – коэффициент, равный:
По таблице 72 [1] по приведенной гибкости вычисляем коэффициент jу = 0,764 и проверяем устойчивость стержня относительно свободной оси:
Устойчивость стержня относительно свободной оси обеспечена.
Расчет планок сквозной колонны
Расчет планок выполняем на условную перерезывающую силу Qfic, которая вычисляется согласно п. 5.8* [1] по формуле:
Условная поперечная сила распределяется поровну между планками и их расчет сводится к расчету элементов безраскосных ферм (рисунок 4.2).
Рисунок 4.2 – К расчету планок сквозной колонны
Планки рассчитываются на следующие усилия: а) на силу среза планки FS, определяемую по формуле:
б) на момент в планке MS
Планка приваривается к полкам двутавров угловыми швами (рисунок 4.3). Задаемся параметрами сварки: сварка полуавтоматическая в среде углекислого газа, положение шва – нижнее, диаметр сварочной проволоки 2 мм. Сварочная проволока марки СВ-08Г2С (таблица 55* [1]), расчетное сопротивление металла шва Rwf = 21,5 кН/см2 (таблица 56 [1]), расчетное сопротивление металла границы сплавлении:
где Run = 37 кН/см2 – нормативное сопротивление листового проката стали С245 толщиной 2...20 мм по временному сопротивлению (таблица 51* [1]). Предварительно задаемся катетом шва kf = 12 мм, тогда коэффициенты проплавления шва по таблице 34* [1] равны bf= 0,8, bz= 1,0. Сравниваем расчетные сопротивления шва с учетом этих коэффициентов:
следовательно, расчет ведем по металлу границы сплавления. Расчетная длина шва при высоте планки hs= 17 см равна:
Определяем напряжения в шве от силы FS:
и от моментаMS:
где момент сопротивления шва:
Суммарные напряжения в шве:
Прочность шва обеспечена.
|


 а) б)
а) б)

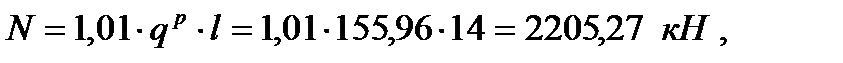
 l = 40 и по таблице 72 [1] определяем значение коэффициента j = 0,894 для стали класса С245 при Ry = 24 кН/см2. Требуемая площадь сечения:
l = 40 и по таблице 72 [1] определяем значение коэффициента j = 0,894 для стали класса С245 при Ry = 24 кН/см2. Требуемая площадь сечения: