Тела действуют друг на друга с силами, равными по модулю и противоположными по направлению.
Силы, возникающие при взаимодействии тел, всегда имеют одинаковую природу. Они приложены к разным телам и поэтому не могут уравновешивать друг друга. Складывать по правилам векторного сложения можно только силы, приложенные к одному телу.
../../../../Program Files/Physicon/Open Physics 2.5 part 1/design/images/Fwd_h.gif../../../../Program Files/Physicon/Open Physics 2.5 part 1/design/images/Bwd_h.gif Вес и невесомость Силу тяжести Весом тела называют силу, с которой тело вследствие его притяжения к Земле действует на опору или подвес. При этом предполагается, что тело неподвижно относительно опоры или подвеса. Пусть тело лежит на неподвижном относительно Земли горизонтальном столе (рис. 1.11.1). Систему отсчета, связанную с Землей, будем считать инерциальной. На тело действуют сила тяжести FT=mg направленная вертикально вниз, и сила упругости Fу=N с которой опора действует на тело. Силу N называют силой нормального давления или силой реакции опоры. Силы, действующие на тело, уравновешивают друг друга: FT=Fу=--N В соответствии с третьим законом Ньютона тело действует на опору с некоторой силой
Если тело неподвижно висит на пружине, то роль силы реакции опоры (подвеса) играет упругая силы пружины. По растяжению пружины можно определить вес тела и равную ему силу притяжения тела Землей. Для определения веса тела можно использовать также рычажные весы, сравнивая вес данного тела с весом гирь на равноплечем рычаге. Приводя в равновесие рычажные весы путем уравнивая веса тела суммарным весом гирь, мы одновременно достигаем равенства массы тела суммарной массе гирь, независимо от значения ускорения свободного падения в данной точке земной поверхности. Например, при подъеме в горы на высоту 1 км показания пружинных весов изменяются на 0,0003 от своего значения на уровне моря. При этом равновесие рычажных весов сохраняется. Поэтому рычажные весы являются прибором для определения массы тела путем сравнения с массой гирь (эталонов). Рассмотрим теперь случай, когда тело лежит на опоре (или подвешено на пружине) в кабине лифта, движущейся с некоторым ускорением a относительно Земли. Система отсчета, связанная с лифтом, не является инерциальной. На тело по-прежнему действуют сила тяжести mg и сила реакции опоры N но теперь эти силы не уравновешивают друг друга. По второму закону Ньютона
Сила P действующая на опору со стороны тела, которую и называют весом тела, по третьему закону Ньютона равна --N Следовательно, вес тела в ускоренно движущемся лифте есть
Пусть вектор ускорения a направлен по вертикали (вниз или вверх). Если координатную ось OY направить вертикально вниз, то векторное уравнение для P можно переписать в скалярной форме:
В этой формуле величины P, g и a следует рассматривать как проекции векторов
Из формулы (*) видно, что если a < g, то вес тела P в ускоренно движущемся лифте меньше силы тяжести. Если a > g, то вес тела изменяет знак. Это означает, что тело прижимается не к полу, а к потолку кабины лифта («отрицательный» вес). Наконец, если a = g, то P = 0. Тело свободно падает на Землю вместе с кабиной. Такое состояние называется невесомостью. Оно возникает, например, в кабине космического корабля при его движении по орбите при выключенных реактивных двигателях. Если вектор ускорения a направлен вертикально вверх, то a < 0 и, следовательно, вес тела всегда будет превышать по модулю силу тяжести. Увеличение веса тела, вызванное ускоренным движением опоры или подвеса, называют перегрузкой. Действие перегрузки испытывают космонавты, как при взлете космической ракеты, так и на участке торможения при входе корабля в плотные слои атмосферы. Большие перегрузки испытывают летчики при выполнении фигур высшего пилотажа, особенно на сверхзвуковых самолетах. ../../../../Program Files/Physicon/Open Physics 2.5 part 1/design/images/Fwd_h.gif../../../../Program Files/Physicon/Open Physics 2.5 part 1/design/images/Bwd_h.gifЗакон всемирного тяготения. По второму закону Ньютона причиной изменения движения, т. е. причиной ускорения тел, является сила. В механике рассматриваются силы различной физической природы. Многие механические явления и процессы определяются действием сил тяготения. Закон всемирного тяготения был открыт И. Ньютоном в 1682 году. Еще в 1665 году 23-летний Ньютон высказал предположение, что силы, удерживающие Луну на ее орбите, той же природы, что и силы, заставляющие яблоко падать на Землю. По его гипотезе между всеми телами Вселенной действуют силы притяжения (гравитационные силы), направленные по линии, соединяющей центры масс (рис. 1.10.1). У тела в виде однородного шара центр масс совпадает с центром шара.
В последующие годы Ньютон пытался найти физическое объяснение законам движения планет, открытых астрономом И. Кеплером в начале XVII века, и дать количественное выражение для гравитационных сил. Зная как движутся планеты, Ньютон хотел определить, какие силы на них действуют. Такой путь носит название обратной задачи механики. Если основной задачей механики является определение координат тела известной массы и его скорости в любой момент времени по известным силам, действующим на тело, и заданным начальным условиям (прямая задача механики), то при решении обратной задачи необходимо определить действующие на тело силы, если известно, как оно движется. Решение этой задачи и привело Ньютона к открытию закона всемирного тяготения. Все тела притягиваются друг к другу с силой, прямо пропорциональной их массам и обратно пропорциональной квадрату расстояния между ними:
Коэффициент пропорциональности G одинаков для всех тел в природе. Его называют гравитационной постоянной
Многие явления в природе объясняются действием сил всемирного тяготения. Движение планет в Солнечной системе, движение искусственных спутников Земли, траектории полета баллистических ракет, движение тел вблизи поверхности Земли – все эти явления находят объяснение на основе закона всемирного тяготения и законов динамики. Одним из проявлений силы всемирного тяготения является сила тяжести. Так принято называть силу притяжения тел к Земле вблизи ее поверхности. Если М – масса Земли, R З – ее радиус, m – масса данного тела, то сила тяжести равна
где g – ускорение свободного падения у поверхности Земли:
Сила тяжести направлена к центру Земли. В отсутствие других сил тело свободно падает на Землю с ускорением свободного падения. Среднее значение ускорения свободного падения для различных точек поверхности Земли равно 9,81 м/с2. Зная ускорение свободного падения и радиус Земли (R З = 6,38·106 м), можно вычислить массу Земли М:
При удалении от поверхности Земли сила земного тяготения и ускорение свободного падения изменяются обратно пропорционально квадрату расстояния r до центра Земли. Рис. 1.10.2 иллюстрирует изменение силы тяготения, действующей на космонавта в космическом корабле при его удалении от Земли. Сила, с которой космонавт притягивается к Земле вблизи ее поверхности, принята равной 700 Н.
Примером системы двух взаимодействующих тел может служить система Земля–Луна. Луна находится от Земли на расстоянии r Л = 3,84·106 м. Это расстояние приблизительно в 60 раз превышает радиус Земли R З. Следовательно, ускорение свободного падения a Л, обусловленное земным притяжением, на орбите Луны составляет
С таким ускорением, направленным к центру Земли, Луна движется по орбите. Следовательно, это ускорение является центростремительным ускорением. Его можно рассчитать по кинематической формуле для центростремительного ускорения:
где T = 27,3 сут – период обращения Луны вокруг Земли. Совпадение результатов расчетов, выполненных разными способами, подтверждает предположение Ньютона о единой природе силы, удерживающей Луну на орбите, и силы тяжести. Собственное гравитационное поле Луны определяет ускорение свободного падения g Л на ее поверхности. Масса Луны в 81 раз меньше массы Земли, а ее радиус приблизительно в 3,7 раза меньше радиуса Земли. Поэтому ускорение g Л определится выражением:
В условиях такой слабой гравитации оказались космонавты, высадившиеся на Луне. Человек в таких условиях может совершать гигантские прыжки. Например, если человек в земных условиях подпрыгивает на высоту 1 м, то на Луне он мог бы подпрыгнуть на высоту более 6 м. Рассмотрим теперь вопрос об искусственных спутниках Земли. Искусственные спутники движутся за пределами земной атмосферы, и на них действуют только силы тяготения со стороны Земли. В зависимости от начальной скорости траектория космического тела может быть различной Мы рассмотрим здесь только случай движения искусственного спутника по круговой околоземной орбите. Такие спутники летают на высотах порядка 200–300 км, и можно приближенно принять расстояние до центра Земли равным ее радиусу R З. Тогда центростремительное ускорение спутника, сообщаемое ему силами тяготения, приблизительно равно ускорению свободного падения g. Обозначим скорость спутника на околоземной орбите через υ1. Эту скорость называют первой космической скоростью. Используя кинематическую формулу для центростремительного ускорения, получим:
Двигаясь с такой скоростью, спутник облетал бы Землю за время На самом деле период обращения спутника по круговой орбите вблизи поверхности Земли несколько превышает указанное значение из-за отличия между радиусом реальной орбиты и радиусом Земли. Движение спутника можно рассматривать как свободное падение, подобное движению снарядов или баллистических ракет. Различие заключается только в том, что скорость спутника настолько велика, что радиус кривизны его траектории равен радиусу Земли. Для спутников, движущихся по круговым траекториям на значительном удалении от Земли, земное притяжение ослабевает обратно пропорционально квадрату радиуса r траектории. Скорость спутника υ находится из условия
Таким образом, на высоких орбитах скорость движения спутников меньше, чем на околоземной орбите. Период T обращения такого спутника равен
Здесь T 1 – период обращения спутника на околоземной орбите. Период обращения спутника растет с увеличением радиуса орбиты. Нетрудно подсчитать, что при радиусе r орбиты, равном приблизительно 6,6 R З, период обращения спутника окажется равным 24 часам. Спутник с таким периодом обращения, запущенный в плоскости экватора, будет неподвижно висеть над некоторой точкой земной поверхности. Такие спутники используются в системах космической радиосвязи. Орбита с радиусом r = 6,6 R 3 называется геостационарной.
../../../../Program Files/Physicon/Open Physics 2.5 part 1/design/images/Fwd_h.gif../../../../Program Files/Physicon/Open Physics 2.5 part 1/design/images/Bwd_h.gif Кинетическая и потенциальная энергии Если тело некоторой массы m двигалось под действием приложенных сил, и его скорость изменилась от υ 1 до υ2,то силы совершили определенную работу A. Между изменением скорости тела и работой, совершенной приложенными к телу силами, существует связь. Эту связь проще всего установить, рассматривая движение тела вдоль прямой линии под действием постоянной силы F. В этом случае векторы силы
Отсюда следует, что
Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела: Работа приложенной к телу равнодействующей силы равна изменению его кинетической энергии.
Это утверждение называют теоремой о кинетической энергии. Теорема о кинетической энергии справедлива и в общем случае, когда тело движется под действием изменяющейся силы, направление которой не совпадает с направлением перемещения. Кинетическая энергия – это энергия движения. Кинетическая энергия тела массой m, движущегося со скоростью
Если тело движется со скоростью
Потенциальная энергия определяется взаимным положением тел (например, положением тела относительно поверхности Земли). Понятие потенциальной энергии можно ввести только для сил, работа которых не зависит от траектории движения тела и определяется только начальным и конечным положениями. Работа консервативных сил на замкнутой траектории равна нулю. Свойством консервативности обладают сила тяжести и сила упругости. Для этих сил можно ввести понятие потенциальной энергии. Если тело перемещается вблизи поверхности Земли, то на него действует постоянная по величине и направлению сила тяжести
где F т = F тy = – mg – проекция силы тяжести, Δ s y – проекция вектора перемещения. При подъеме тела вверх сила тяжести совершает отрицательную работу, так как Δ s y > 0. Если тело переместилось из точки, расположенной на высоте h 1, в точку, расположенную на высоте h 2 от начала координатной оси OY (рис. 1.19.3), то сила тяжести совершила работу
Эта работа равна изменению некоторой физической величины mgh, взятому с противоположным знаком. Эту физическую величину называют потенциальной энергией тела в поле силы тяжести
Она равна работе, которую совершает сила тяжести при опускании тела на нулевой уровень. Работа силы тяжести равна изменению потенциальной энергии тела, взятому с противоположным знаком.
Потенциальная энергия E p зависит от выбора нулевого уровня, т. е. от выбора начала координат оси OY. Физический смысл имеет не сама потенциальная энергия, а ее изменение Δ E p = E p2 – E p1 при перемещении тела из одного положения в другое. Это изменение не зависит от выбора нулевого уровня. ../../../../Program Files/Physicon/Open Physics 2.5 part 1/design/images/buttonModel_h.gif Если рассматривать движение тел в поле тяготения Земли на значительных расстояниях от нее, то при определении потенциальной энергии необходимо принимать во внимание зависимость силы тяготения от расстояния до центра Земли (закон всемирного тяготения). Для сил всемирного тяготения потенциальную энергию удобно отсчитывать от бесконечно удаленной точки, т. е. полагать потенциальную энергию тела в бесконечно удаленной точке равной нулю. Формула, выражающая потенциальную энергию тела массой m на расстоянии r от центра Земли, имеет вид (см. §1.24):
где M – масса Земли, G – гравитационная постоянная. Понятие потенциальной энергии можно ввести и для упругой силы. Эта сила также обладает свойством консервативности. Растягивая (или сжимая) пружину, мы можем делать это различными способами. Можно просто удлинить пружину на величину x, или сначала удлинить ее на 2 x, а затем уменьшить удлинение до значения x и т. д. Во всех этих случаях упругая сила совершает одну и ту же работу, которая зависит только от удлинения пружины x в конечном состоянии, если первоначально пружина была недеформирована. Эта работа равна работе внешней силы A, взятой с противоположным знаком:
где k – жесткость пружины. Растянутая (или сжатая) пружина способна привести в движение прикрепленное к ней тело, т. е. сообщить этому телу кинетическую энергию. Следовательно, такая пружина обладает запасом энергии. Потенциальной энергией пружины (или любого упруго деформированного тела) называют величину
Потенциальная энергия упруго деформированного тела равна работе силы упругости при переходе из данного состояния в состояние с нулевой деформацией. Если в начальном состоянии пружина уже была деформирована, а ее удлинение было равно x 1, тогда при переходе в новое состояние с удлинением x 2 сила упругости совершит работу, равную изменению потенциальной энергии, взятому с противоположным знаком:
Потенциальная энергия при упругой деформации – это энергия взаимодействия отдельных частей тела между собой силами упругости. Свойством консервативности обладают наряду с силой тяжести и силой упругости некоторые другие виды сил, например, сила электростатического взаимодействия между заряженными телами. Сила трения не обладает этим свойством. Работа силы трения зависит от пройденного пути. Понятие потенциальной энергии для силы трения вводить нельзя. ../../../../Program Files/Physicon/Open Physics 2.5 part 1/design/images/Fwd_h.gif../../../../Program Files/Physicon/Open Physics 2.5 part 1/design/images/Bwd_h.gifЗакон сохранения механической энергии
|


 с которой тела притягиваются к Земле, нужно отличать от веса тела. Понятие веса широко используется в повседневной жизни.
с которой тела притягиваются к Земле, нужно отличать от веса тела. Понятие веса широко используется в повседневной жизни. равной по модулю силе реакции опоры и направленной в противоположную сторону: P=--N По определению, сила P и называется весом тела. Из приведенных выше соотношений видно, что P=FT=mg т. е. вес тела P равен силе тяжести mg. Но эти силы приложены к разным телам!
равной по модулю силе реакции опоры и направленной в противоположную сторону: P=--N По определению, сила P и называется весом тела. Из приведенных выше соотношений видно, что P=FT=mg т. е. вес тела P равен силе тяжести mg. Но эти силы приложены к разным телам!


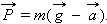
 ,
, 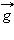 и
и  на ось OY. Так как эта ось направлена вертикально вниз, g = const > 0, а величины P и a могут быть как положительными, так и отрицательными. Пусть, для определенности, вектор ускорения a направлен вертикально вниз, тогда a > 0 (рис. 1.11.2).
на ось OY. Так как эта ось направлена вертикально вниз, g = const > 0, а величины P и a могут быть как положительными, так и отрицательными. Пусть, для определенности, вектор ускорения a направлен вертикально вниз, тогда a > 0 (рис. 1.11.2).














 перемещения s,скорости υ и ускорения a направлены вдоль одной прямой, и тело совершает прямолинейное равноускоренное движение. Направив координатную ось вдоль прямой движения, можно рассматривать F, s, υ и a как алгебраические величины (положительные или отрицательные в зависимости от направления соответствующего вектора). Тогда работу силы можно записать как A = Fs. При равноускоренном движении перемещение s выражается формулой
перемещения s,скорости υ и ускорения a направлены вдоль одной прямой, и тело совершает прямолинейное равноускоренное движение. Направив координатную ось вдоль прямой движения, можно рассматривать F, s, υ и a как алгебраические величины (положительные или отрицательные в зависимости от направления соответствующего вектора). Тогда работу силы можно записать как A = Fs. При равноускоренном движении перемещение s выражается формулой
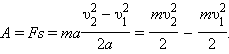

 равна работе, которую должна совершить сила, приложенная к покоящемуся телу, чтобы сообщить ему эту скорость:
равна работе, которую должна совершить сила, приложенная к покоящемуся телу, чтобы сообщить ему эту скорость:

 Работа этой силы зависит только от вертикального перемещения тела. На любом участке пути работу силы тяжести можно записать в проекциях вектора перемещения
Работа этой силы зависит только от вертикального перемещения тела. На любом участке пути работу силы тяжести можно записать в проекциях вектора перемещения  на ось OY, направленную вертикально вверх:
на ось OY, направленную вертикально вверх:







