Доходность ценной бумаги и портфеля
Анализ теоретической и практической работы с типовыми моделями портфельного анализа применительно к современным российским условиям приводит к следующим выводам [11, с. 147-148]: 1. Применять подобные модели можно и нужно, но только при условии их глубокой адаптации к российской специфике. 2. Хороший стратегический результат, как правило, можно получить только в случае адекватной уникальной адаптации той или иной типовой модели к данной конкретной ситуации, то есть конкретная бизнес-ситуация практически всегда требует именно уникальной модификации конкретной модели. 3. Положительный эффект от типовых моделей можно достичь в результате достаточно долгой, напряженной и творческой работы команды высококвалифицированных профессионалов, в которую обязательно должны входить как серьезные специалисты по стратегическому управлению, так и настоящие знатоки именно данного конкретного бизнеса. Когда такой команды нет, то даже при очень большом желании от использования типовых моделей следует отказаться; а соответствующие проблемы попытаться решить другими более простыми инструментами. 4. Правильное практическое применение любой типовой модели портфельного анализа – это не только весьма сложное дело, но и почти всегда достаточно дорогое удовольствие.
ЛИТЕРАТУРА
1. Ансофф И. Новая корпоративная стратегия. – СПб.: Питер Ком, 1999. – 416 с. (Глава 9 Портфельный анализ. С. 217-236) 2. Бодди Д., Пэйтон Р. Основы менеджмента: пер. с англ. – СПб.: Изд-во «Питер», 1999. – 816 с. (с. 423-426 «Портфельные модели») 3. Вествуд Дж. Маркетинговый план. – СПб.: Питер, 2001. – 256 с. (Раздел 6.2 Товарный портфель с. 112-122) 4. Виханский О.С. Стартегическое управление: Учебник. – М.: Гардарика, 1998. – 296 с. (Раздел 8.2 Анализ портфеля продукции с. 191-197) 5. Дорошев В.И. Введение в теорию маркетинга: Учебное пособие. – М.: ИНФРА-М, 2000. – 285 с. (Раздел 7.13 Распределение ресурсов для СБЕ. С. 171-222) 6. Ефремов В.С. Стратегия бизнеса. Концепции и методы планирования. – М.: Изд-во «Финпресс», 1998. – 192 с. (Раздел 2 Стратегическое планирование на уровне корпорации. С. 56-110) 7. Ламбен Жан-Жак Стратегический маркетинг. Европейская перспектива. Пер. с франц. – СПб.: Изд-во Наука, 1996. – 589 с. (Раздел 9.1 Анализ портфеля направлений деятельности с. 313-328) 8. Мак Дональд М. Стратегическое планирование маркетинга. – СПб.: Изд-во «Питер», 2000. – 320 с. (с. 96-104, 123-126, 239-244) 9. Маркова В.Д., Кузнецова С.А. Стратегический менеджмент: курс лекций. – М.: ИНФРА-М; Новосибирск: Сибирское соглашение, 1999. – 288 с. (Глава 5 Портфельный анализ. с. 90-124) 10. Минцберг Г., Альстрэнд Б., Лэмпел Дж. Школы стратегий. Пер. с англ. – СПб.: Изд-во «Питер», 2000. – 336 с. 11. Попов С.А. Стратегическое управление: 17- модульная программа для менеджеров «Управление развитием организации». Модуль 4. – М.: ИНФРА-М, 2000. – 304 с. (Раздел 3.2.3 Система бизнес-стратегий: типовые модели. с. 126-148) 12. Томпсон А.А. мл., Стрикленд А.Дж. III Стратегический менеджмент: концепции и ситуации: Учебник для вузов. Пер. с 9-го англ. изд. М.: ИНФРА-М, 2000. – 412 с. (Глава 8 Стратегический анализ диверсифицированных компаний. С. 287-302) Доходность ценной бумаги и портфеля Рынок ценных бумаг будем рассматривать как статический и будем исследовать его функционирование на фиксированном интервале времени, в течение которого инвестор владеет ценной бумагой, стоимость которой в начале интервала обозначим
Если не рассматривать дивиденды и другие величины, от которых зависит доходность (инфляция и т.п.), то формула (1) принимает максимально простой вид:
Портфелем, состоящим из n видов ценных бумаг, называют вектор
где Доходностью портфеля X называют величину:
где Доходность портфеля X выражается формулой:
где Стоимости ценных бумаг в начале периода Эффективность портфеля (или ожидаемая доходность портфеля)
где Обозначим через
Дисперсия или квадрат риска
где Таким образом, с каждым портфелем X связаны две величины: эффективность (ожидаемая доходность) μ и риск σ. Инвестор хотел бы иметь такой портфель, который обеспечивал бы наибольшую ожидаемую доходность при минимальном риске. Такая задача, однако, противоречива, поскольку, вообще говоря, большая ожидаемая доходность влечет за собой увеличение риска. Поэтому можно рассмотреть следующие задачи: 1. Найти портфель минимального риска при заданной его эффективности (при эффективности не менее заданной, при произвольной эффективности). 2. Найти портфель максимальной эффективности при минимальном риске (при риске, не превышающем данный уровень).
|

 , в конце интервала –
, в конце интервала –  . Пусть d – дивиденды, выплаченные за рассматриваемый промежуток времени. Тогда д оходностью ценной бумаги за этот интервал времени называется величина:
. Пусть d – дивиденды, выплаченные за рассматриваемый промежуток времени. Тогда д оходностью ценной бумаги за этот интервал времени называется величина: (1)
(1)
 (2)
(2) – доля инвестиций в ценные бумаги вида i.
– доля инвестиций в ценные бумаги вида i. (3)
(3) –стоимость портфеля в начале периода,
–стоимость портфеля в начале периода,  – в конце периода;
– в конце периода;  – дивиденды, полученные по всем бумагам портфеля.
– дивиденды, полученные по всем бумагам портфеля. (4)
(4) – доходности ценных бумаг, входящих в портфель X.
– доходности ценных бумаг, входящих в портфель X. – детерминированные величины, в то время как в конце периода они уже являются случайными величинами, поэтому и доходности отдельных ценных бумаг и доходность всего портфеля являются случайными величинами. Обозначим их заглавными буквами
– детерминированные величины, в то время как в конце периода они уже являются случайными величинами, поэтому и доходности отдельных ценных бумаг и доходность всего портфеля являются случайными величинами. Обозначим их заглавными буквами  и
и  . Математическое ожидание доходности ценной бумаги называется ее эффективностью, а математическое ожидание доходности портфеля называется эффективностью портфеля.
. Математическое ожидание доходности ценной бумаги называется ее эффективностью, а математическое ожидание доходности портфеля называется эффективностью портфеля. вычисляется по формуле:
вычисляется по формуле: (5)
(5) – эффективности ценных бумаг (математические ожидания доходностей
– эффективности ценных бумаг (математические ожидания доходностей  , составляющих портфель.
, составляющих портфель. – вектор эффективностей (ожидаемых доходностей) портфеля X, тогда формулу (5) можно записать в матричных обозначениях следующим образом:
– вектор эффективностей (ожидаемых доходностей) портфеля X, тогда формулу (5) можно записать в матричных обозначениях следующим образом: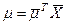 (6)
(6)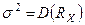 доходности портфеля
доходности портфеля  (7)
(7) ‑ковариационная матрица случайных величин
‑ковариационная матрица случайных величин  .
.


