Порядок выполнения типового расчета по этапам

I этап. Провести первичную обработку опытных данных и высказать предположение о законе распределения исследуемой случайной величины:

а) составить интервальные статистические ряды распределения частот;

разряды	I1	I2	I3	I4	I5	I6	I7	I8
число паподаний
относ. Част.разряда	0,22	0,22	0,16	0,12	0,12	0,08	0,05	0,05
плотность частоты	0,448	0,448	0,326	0,244	0,244	0,163	0,102	0,102

 

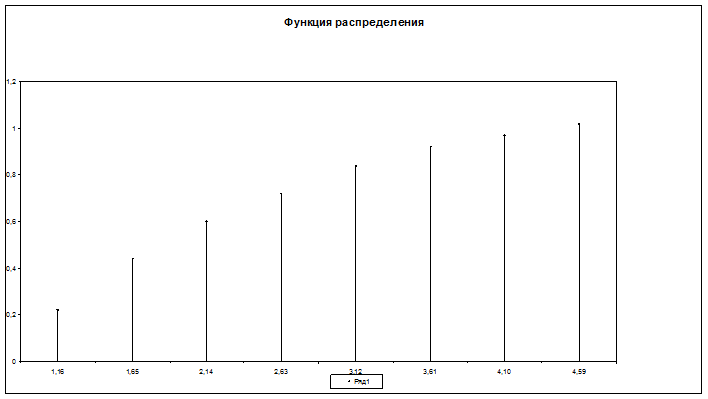
б) построить эмпирическую функцию распределения и гистограмму;

в) записать в общем виде предполагаемый закон распределения исследуемой случайной величины.

II этап. Рассчитать оценки числовых характеристик выборки и определить параметры гипотетического распределения:

а) вычислить статистическое среднее, дисперсию, среднее квадратичное отклонение, коэффициент асимметрии, эксцесс, коэффициент вариации, моду, медиану и средние квадратичные ошибки определения асимметрии и эксцесса;

статис.среднее	2,373
Дисперсия (S^2)	1,043
Сред. Квад. отклонение s	1,021
коэфф.асимметрия(sk)	0,496
Эксцесс (Ex	-0,767
Вариации(u)	0,430
мода 1	1,157
мода 2	1,648
медиана Ме	1,648
Сред.квад.ошибки опред асимметрии sA	0,239
Сред.квад.ошибки опред эксцесса sE	0,464
несмещ диспр. s^2	1,054
s	1,027

 

б) найти доверительные интервалы для математического ожидания и среднего квадратичного отклонения с заданной надежностью (взять два значения надежности b = 0,9 и b = 0,95 и сравнить доверительные интервалы);

b = 0,9

2,201

<M[X]<

2,545

0,916

< s<

1,157

b = 0,95

2,168

<M[X]<

2,578

0,897

< s<

1,186

 

в) определить параметры и записать теоретический закон распределения исследуемой случайной величины.

III этап. Проверить близость эмпирического и теоретического законов распределения:

а) построить на одном графике эмпирический и теоретический законы распределения;

б) проверить близость эмпирического и теоретического распределений с помощью критерия Пирсона;

c^2

5,5831

При a = 0,01 и a = 0,05 гипотеза подтверждается.

в) проверить близость эмпирического и теоретического распределений по критерию Колмогорова (взять два уровня значимости a = 0,01 и a = 0,05; результаты сравнить).

max разница	0,252743
l=	2,527434

Получили, что при значении a = 0,01 и a = 0,05 гипотеза отвергается.

IV этап. Изучить связь между двумя случайными величинами X и Y:

а) рассчитать оценки числовых характеристик двумерной случайной величины (X, Y), проверить значимость коэффициента корреляции;

для У:

представ.разряда	1,092	1,347	1,602	1,857	2,113	2,368	2,751
относ. Част.разряда	0,23	0,23	0,13	0,13	0,09	0,08	0,08
статис.среднее	1,610
S^2	0,258
s	0,508
sk асимметрия	0,994
Ex эксцесс	-0,220
u вариации	0,316
мода 1	1,347
мода 1	1,347
медиана Ме	1,347
sA	0,239
sE	0,464
несмещ диспр. s=	0,261
s	0,511
rxy	0,225

 

б) найти эмпирические функции линейной регрессии составляющих двумерной случайной величины;

в) построить корреляционное поле и графики функции регрессии на одном рисунке.

Замечание 1. Часто оптимальная длина h интервала разбиения выборочных значений выбирается согласно формулы h = (x _max – x _min)/(1 + 3,32 lg n), где x _max и x _min – соответственно наибольшее и наименьшее выборочные значения, n – объем выборки.

Замечание 2. Средние квадратичные ошибки определения асимметрии s_A и эксцесса s_E равны соответственно: s_A = , s_E = .