Метод конечных разностей
Лабораторная работа №6 «Методы конечных разностей»
Выполнила: Жакупова А.Б CS 111 A
Проверил: Рысбайулы Б. Р.
Алматы 2013г.
Метод конечных разностей Постановка задачи: Метод контрольного объема:
(1)-Закон сохранения энергии
(1)-(2) –краевая задача
Точн. Приближенное значение температуры воды:
********
Надо найти Т(х), особенно
(1)- (2) –дифференциальная краевая задача (3)-(4) – разностная краевая задача Метод Томаса (прогонка) (3) записываем в стандартной форме
(5)- стандартная форма
(7) – подставляем в (5):

(5) = (7)È (8)
**
(7) -> i=n =>
Theorem: Если B>A+C, #include <iostream> #include <string> #include <cmath> #include <fstream>
using namespace std;
const double k = 0.6; // коэф. теплопроводности воды (Ватт/м*Кельвин) const double Cro = 4.094*1000; // коэф. теплоемкости трубы (Дж/кг*К) const double ro = 0.97; // плотрость воды (кг/м^3) const double u = 3; // скорость воды в трубе (м/с) const double H = 0.2; // толщина изоляций (м) const double V = 0.03; // коэф. теплопроводности стекловаты const double hc = V / H; // коэф. теплоотдачи в окруж. среду
const double R = 0.3; // радиус трубы (м) const int l = 5000; // длинна трубы (м) const int n = 1000; // число разбиений (м) const int Dx = l / n; // шаги
const int To = 95; // начальная температура
const double M = (ro*Cro*u) / k; const double N = (2*hc) / (R*k); double Alf[n],Bet[n],F[n],y[n],Tv1[n];
double Tv(double a){
if (a<=l/2) { return (48+((a - l/4) / (l/4)));} else { return (49+18*((a - l/2) / (l/4)));} } void GoToFile(double x) { ofstream file; file.open("results.txt", fstream::out | fstream::app); file<<x<<" "; file<<"\n";
file.close(); } int main (int argc, char *argv[]) { Alf[1] = 0; Bet[1] = To; y[0] = To;
double A = 1 + M*Dx; double B = 2 + M*Dx+N*Dx*Dx; double C = 1;
for(int i=1; i<n; i++){ F[i] = N*Dx*Dx*Tv(i*Dx); } for(int i = 1; i < n; i++){ Alf[i+1] = A / (B - C*Alf[i]); Bet[i+1] = (C*Bet[i] + F[i]) / (B - C*Alf[i]); }
y[n] = Bet[n] / (1 - Alf[n]); for(int i = n; i > 1; i--){ y[i-1] = Alf[i]*y[i] + Bet[i]; }
for(int i=0; i<=n; i++){ cout<<y[i]<<"\t"<<y[l/2+i]<<endl; if (i==l/2+1) break; if(i%2 ==0) GoToFile(y[i]);
//GoToFile(Tv(i*Dx)); }
system("pause"); return 0; }
Вывод: Если у меня начальная температура Т0 = 95 и при линейной интерполяции -Тв = 48 при х=l/4 -Тв = 49 при х=l/2 -Тв = 67 при х=3l/4
|






 (2)
(2)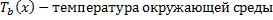
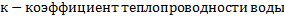





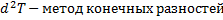
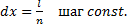
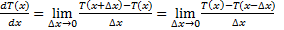
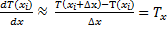 - правая разностная
- правая разностная - левая разностная
- левая разностная
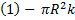
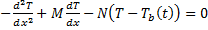
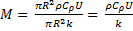
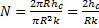





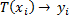


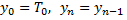

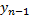

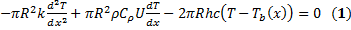






 (4)
(4)




 (7)
(7)

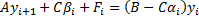



 это равенство выполняется для любого
это равенство выполняется для любого 




 то все
то все 
 ;
;



