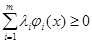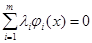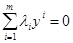Математическая модель персептрона Розенблатта. Обучение персептрона Розенблатта.
Рассмотрим математическую модель персептрона: 1. В рецепторном поле образуется сигнал, соответствующий внешнему раздражителю, который изображается некоторым вектором х. Розенблатт отмечает, что каждое нервное окончание передает достаточно простой сигнал — либо посылает импульс, либо не посылает его. Это означает, что вектор х бинарный, т. е. его координаты могут принимать только два значения: 0 и 1. 2. Набор импульсов распространяется до тех пор, пока с помощью нейронов второго слоя не будет преобразован в новый набор импульсов (бинарный вектор x преобразуется в бинарный вектор y). Розенблатт уточняет характер преобразований у =f(x): а) преобразование осуществляется пороговыми элементами; б) входы преобразующих пороговых элементов соединены с рецепторами случайно. 3. Считается, что персептрон относит входной вектор к p -му понятию, если возбуждается p- й реагирующий нейрон и не возбуждаются другие реагирующие нейроны. Формально это означает, что для вектора
В этих неравенствах 4. Формирование понятий в схеме Розенблатта сводится к образованию коэффициентов (весов) каждого из элементов R. Процедура построения весов элементов R такова. Пусть к данному моменту существуют некоторые веса элементов R и Случай первый. Вектор х соответствует понятию р. Тогда правильной реакцией элемента
Если веса элемента
то веса элемента
Случай второй. Вектор х не соответствует понятию р. Тогда элемент
Если веса элемента
то веса
При обучении аналогично меняются веса всех элементов R персептрона. Розенблатт надеялся, что его персептрон моделирует существенные черты человеческого восприятия, в особенности восприятия зрительных образов. Он полагал, что персептрон легко можно будет обучить узнаванию одного и того же изображения независимо от масштаба изображения, существенных сдвигов его в рецепторном поле и других преобразований, при которых человек относит изображение к одному и тому же понятию. Иными словами, предполагалось, что персептрон будет узнавать предметы инвариантно по отношению к определенным группам преобразований. В действительности же теоретические и экспериментальные исследования персептрона Ф. Розенблатта показали его неспособность к такому обобщению. Последовали всевозможные усложнения схемы персептрона. Строились персептроны с большим числом нейронных слоев, допускалась настройка коэффициентов усиления не только на верхнем слое, но и на промежуточных уровнях, предлагалось вводить перекрестные и обратные связи. Теоретическое исследование таких сложных персептронных схем чрезвычайно затруднительно. На практике же при распознавании зрительных образов эти модели оказались малоэффективными, в конце концов, от них пришлось отказаться и пойти другим путем. Основная идея нового направления состоит в том, чтобы, опираясь на известные свойства зрительных образов, найти такую систему признаков или, общее, такой язык описания изображения, которые уже сами по себе обеспечивают инвариантность по отношению к требуемым преобразованиям. Таким образом, при построении обучающегося устройства закладываются априорные сведения относительно того, по каким именно преобразованиям должна достигаться инвариантность. Если предположить, что физиологическая модель человеческого восприятия действительно аналогична персептрону, то следует допустить, что связи преобразующих 4-элементов с рецепторами (а вероятнее, нескольких слоев таких элементов) отнюдь неслучайны, а построены именно так, чтобы обеспечить новое описание изображения, содержащее уже требуемые инварианты.Математически это означает, что преобразование
таково, что среди координат вектора у есть такие, которые не меняются при определенных преобразованиях вектора х. Возможно, что человек вовсе и не учится находить эти инварианты. Способность использовать их дана ему от рождения и заложена в «схеме» зрительного анализатора, возникшего в процессе эволюции. Во всяком случае эксперименты с персептронами, где в процессе обучения выбиралось и отображение Поэтому, оставляя в стороне вопрос о том, как устроено отображение, будем рассматривать более общую схему персептрона. Будем считать, что дано некоторое преобразование
Здесь х — входной вектор, соответствующий исходному описанию объекта. Преобразование Координаты вектора у теперь в общем случае — действительные числа, не обязательно 0 или 1. Для простоты будем считать, что различаются всего два понятия. Тогда персептрон отнесет вектор х к первому понятию, если выполнится неравенство
а в противном случае — ко второму. Такая схема имеет простую геометрическую интерпретацию: в пространстве Х задана гиперповерхность
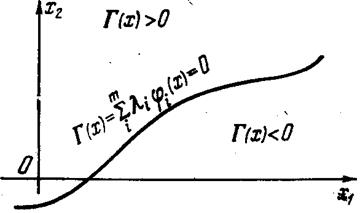
которая делит пространство на два полупространства. Считается, что если вектор х находится по одну сторону от поверхности (это значит, что для него выполняется неравенство (8.2)), то он соответствует первому понятию, если же по другую от нее сторону, то второму. Такие гиперповерхности называются разделяющими (рис. 8.2).
Рис. 8.2.
Для образования нового понятия надо построить соответствующую разделяющую гиперповерхность. Каждой гиперповерхности (8.3) пространства Х в пространстве Y с координатами
Введение пространства Y позволяет заменять рассмотрение разделяющих гиперповерхностей (8.3) разделяющими гиперплоскостями (8.4). Поэтому пространство векторов Y получило название спрямляющего. В спрямляющем пространстве изучается следующая схема. Каждому объекту ставится в соответствие вектор
и ко второму, если по другую.
|

 выполняется система неравенств:
выполняется система неравенств: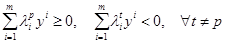
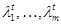 — коэффициенты усиления t -го реагирующего нейрона.
— коэффициенты усиления t -го реагирующего нейрона.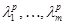 веса р -го элемента
веса р -го элемента 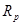 . В момент времени
. В момент времени 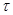 для классификации на вход персептрона поступает сигнал, описываемый вектором
для классификации на вход персептрона поступает сигнал, описываемый вектором 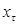 . Вектор
. Вектор 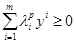 .
.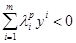
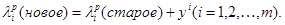

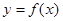
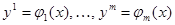 .
. ставит ему в соответствие некоторое новое описание у. Это преобразование выбирается до начала обучения и может быть построено на основании известных сведений о природе данной задачи распознавания.
ставит ему в соответствие некоторое новое описание у. Это преобразование выбирается до начала обучения и может быть построено на основании известных сведений о природе данной задачи распознавания.