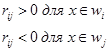Простая модель распознавания образов.

Простая схема распознава­ния содержит два основных блока: датчик и классификатор.

Датчик представляет собой устройство, преобразующее физиче­ские характеристики объекта, подлежащего распознаванию, в набор признаков , которые характеризуют дан­ный объект. Классификатор представляет собой устройство, от­носящее каждый поступающий на его вход допустимый набор значений к одному из конечного числа классов (категорий), вычислив множество значений решающих функций.

Считается, что система распознавания допускает ошибку в том случае, если она относит к классу w_j объект, на самом деле принадлежащий отличному от w_j классу. Считается, что система распознавания R₁ лучше системы распознавания R₂, если вероятность совершить ошибку для системы R₁ меньше, чем для системы R₂. Датчик выдает информацию в виде вектора , где п— число измеренных характеристик каждого физического объекта. Предполагается, что вектор из­мерений х принадлежит одному из М классов образов w₁, w₂,..., w_m.

Принимаем допущение о том, что априорные вероятности появления объектов каждого класса одинаковы, т. е. вектор х может с равной вероятностью относиться как к одному, так и к другому классу. Пусть р(х | w_i)=p_i(х) есть плотность рас­пределения для вектора х при условии, что он принадлежит классу w_i. В таком случае вероятность того, что на самом деле вектор х принадлежит классу w_j, определяется выражением

.

Вероятность того, что вектор х не принадлежит классу w_j, опре­деляется выражением

,

задающим вероятность ошибки.

Решающая функция представляет собой функцию d(x), от­носящую х точно к одному из М заданных классов. Оптимальной считается решающая функция d°(x), которая дает наименьшую вероятность ошибки при всех допустимых значениях х,Значение j, при котором величина 1 – р_j, будет наименьшей, совпадает с тем значением j, которому соответствует наибольшее значение вероятности р(х|w_j). Итак, оптимальная решающая функция d°(x) относит набор х к классу w_i в том и только том случае, если выполняются неравенства

или

.

При р(х|w_i)=р(х|w_k) и р(х|w_i)>р(х|w_j), j=1, 2,.... M, j¹i¹k, оптимальная решающая функция d°(х) может отне­сти вектор х как к классу w_i, так и к классу w_k. Для заданного значения х классификатор определяет оптимальную решающую функцию.

Допустим, наконец, что измеренные значения распределены нормально и соответствующие ковариационные матрицы имеют вид

,

где c_ij – ковариация i -й и j -й компонент вектора измерений x, а c_ij – дисперсия i -й компоненты измерений x. Поскольку в случае нормального распределения имеем

,

где m_i – вектор математического ожидания, отношение двух плотностей p(x|w_i) и p(x|w_j) определяется выражением

Так как ковариационная матрица симметрична, данное отношение условных вероятностей сводится к следующему:

.

Введем величину

;

тогда получим выражения для разделяющей функции

.

Для определения оптимальной разделяющей функции следует вычислить М(М–1) значений функций r_ij(х) для всех i, j, i¹j и выбрать наибольшее из полученных значений. Если окажется что этот максимум равен r_kj, то относим х к классу w_k. Схема оптимального распознавания, воспроизводящая описанный ме­тод, приведена на рис. 10.6.

Отметим,что уравнение описывает гиперплоскость, проведенную в n -мерном простран­стве и разделяющую его в случае наличия двух классов на две части:

Следовательно, уравнение r_ij=0 определяет разделяющую по­верхность для i -го и j -го классов образов.

Рис. 10.6. Пример простой схемы распознавания образов.

 

 

Образ – это описание любого элемента как представителя соот­ветствующего класса образов. В случае, когда множество обра­зов разделяется на непересекающиеся классы, желательно использовать для отнесения этих образов к соответствующим классам какое-либо автоматическое устройство. Считывание и обработка погашенных банковских чеков являются примером задачи распознавания образов. Подобные задачи могут вы­полняться и людьми; машина, однако, справляется с ними много быстрее. С другой стороны, некоторые задачи распознавания таковы, что человек едва ли в состоянии решать их. Примером задач такого рода служит выделение из множества морских сигналов и шумов тона подводной лодки посредством анализа подводных звуковых сигналов.