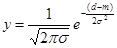Определения формального и искусственного нейрона, искусственной нейронной сети. Функции активации искусственного нейрона.
Определение 2.1. Формальным нейроном называется элемент с m входами и одним выходом d. Он характеризуется m+1 числом: порогом Q и весами Введем обозначения:
d(t)=0 для «выход не возбужден в момент t», d(t)=1 для «выход возбужден в момент t». Тогда приведенное выше правило формально можно записать следующим образом: d(n+1)=1 тогда и только тогда, когда
Заметим, что положительный вес Пользуясь этой крайне упрощенной моделью нейрона, определим теперь модель нервной сети. Определение 2.2. Нейронной сетью называется множество нейронов, соединенных между собой так, что выход каждого нейрона ветвится на подходящее число линий, каждая из которых присоединяется к некоторому входу какого-либо нейрона. Выход каждого нейрона может быть соединен с любым числом входов, но каждый вход не может быть соединен более чем с одним выходом. Все нейроны сети работают в одной и той же шкале времени. Входными линиями сети называются те входы В сети, показанной на рис. 2.3, имеются три входные и четыре выходные линии. Отметим, что входные линии могут ветвиться, а выходные линии не обязаны идти от различных нейронов. Прежде чем приступить к изучению этой модели, укажем на то, что она получена при следующих весьма существенных ограничениях: а) предполагалось, что все нейроны работают синхронно; б) предполагалось, что порог и вес каждого нейрона не меняются с течением времени; в) мы не учитывали химических воздействий (например, алкоголя) и влияния гормонов на изменение поведения мозга; г) мы пренебрегли всеми взаимодействиями между нейронами (например, с помощью электрического поля, возникающего в результате импульсов), кроме синапсических; д) нами игнорировались глиальные клетки.
Рис. 2.3. Простая нейронная сеть.
Этот список ограничений можно продолжить. Отсюда следует, что предложенная модель является только отправным пунктом для изучения и, конечно, далека от окончательной. Другие модели.
Рис. 2.4. Искусственный нейрон.
Функционирование нейрона определяется формулами:
где
d - взвешенная сумма входных сигналов,
F – нелинейная функция.
Рис. 2.4. Виды функций активации.
Жесткая ступенька.
Используется в классическом нейроне. Функция вычисляется двумя тремя машинными инструкциями, поэтому нейроны с такой нелинейностью требуют малых вычислительных затрат. Эта функция чрезмерно упрощена и не позволяет моделировать схемы с непрерывными сигналами. Отсутствие первой производной затрудняет применение градиентных методов для обучения таких нейронов. Сети на классических ФН чаще всего формируются, синтезируются, т.е. их параметры рассчитываются по формулам, в противоположность обучению, когда параметры подстраиваются итеративно.
Логистическая функция.
Применяется очень часто для многослойных перцептронов и других сетей с непрерывными сигналами. Гладкость, непрерывность функции – важные положительные качества. Непрерывность первой производной позволяет обучать сеть градиентными методами (например, метод обратного распространения ошибки). Функция симметрична относительно точки (d=0, y=1/2),это делает равноправными значения y=0 и y=1, что существенно в работе сети. Тем не менее, диапазон выходных значений от 0 до 1 несимметричен, из-за этого обучение значительно замедляется. Данная функция – сжимающая, т.е. для малых значений d коэффициент передачи K=y/d велик, для больших значений он снижается. Поэтому диапазон сигналов, с которыми нейрон работает без насыщения, оказывается широким. Значение производной легко выражается через саму функцию. Быстрый расчет производной ускоряет обучение. Гиперболический тангенс.
Тоже применяется часто для сетей с непрерывными сигналами. Функция симметрична относительно точки (0,0), это преимущество по сравнению с сигмоидой. Производная также непрерывна и выражается через саму функцию.
Пологая ступенька.
Рассчитывается легко, но имеет разрывную первую производную в точках
Гауссова кривая.
Применяется в случаях, когда реакция нейрона должна быть максимальной для некоторого определенного значения d.
Линейная функция.
Применяется для тех моделей сетей, где не требуется последовательное соединение слоев нейронов друг за другом. Выбор функции активации определяется: спецификой задачи; удобством реализации; алгоритмом обучения.
|

 . Каждому входу
. Каждому входу  сопоставляется вес
сопоставляется вес 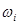 . Нейрон работает в дискретном времени t= 1, 2, 3, 4,... Его выход в момент п+ 1 зависит только от входов в момент п. Эта зависимость задается следующим правилом (сравнить с утверждением (2.1)): нейрон в момент п+1 передает импульс по своему аксону в том и только в том случае, когда сумма всех весов возбужденных входов в момент п превышает порог нейрона.
. Нейрон работает в дискретном времени t= 1, 2, 3, 4,... Его выход в момент п+ 1 зависит только от входов в момент п. Эта зависимость задается следующим правилом (сравнить с утверждением (2.1)): нейрон в момент п+1 передает импульс по своему аксону в том и только в том случае, когда сумма всех весов возбужденных входов в момент п превышает порог нейрона.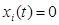 для «i -й вход не возбужден в момент t»,
для «i -й вход не возбужден в момент t», для «i -й вход возбужден в момент t»,
для «i -й вход возбужден в момент t», .
.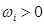 указывает на то, что i -й вход (синапс) является возбуждающим, а отрицательный вес
указывает на то, что i -й вход (синапс) является возбуждающим, а отрицательный вес 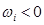 означает, что i -й вход является тормозящим входом.
означает, что i -й вход является тормозящим входом.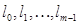 нейронов сети, которые не подсоединены к выходам нейронов. Выходными линиями сети называются те линии
нейронов сети, которые не подсоединены к выходам нейронов. Выходными линиями сети называются те линии  выходов нейронов, которые не соединены с входами нейронов.
выходов нейронов, которые не соединены с входами нейронов.

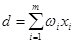

 - пороговый уровень нейрона,
- пороговый уровень нейрона,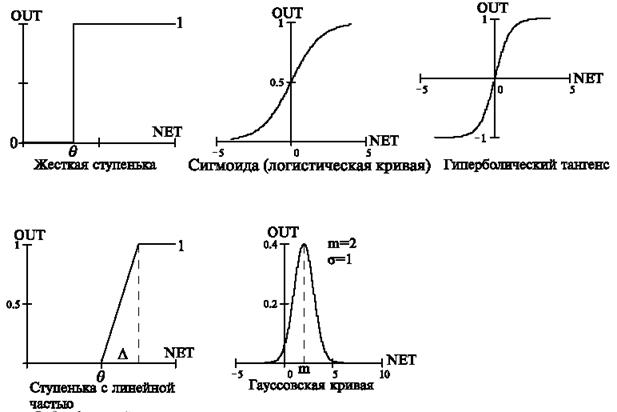

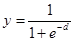


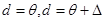 , что усложняет алгоритм обучения.
, что усложняет алгоритм обучения.