Умножение вектора на число
Произведение вектора a на число λ — это коллинеарный ему вектор λa, со направленный с вектором a, если λ > 0, и направленный противоположно к нему, если λ < 0. Если λ = 0,то λa = 0. Модуль вектора λa: |λa| = |λ| |a|.
Скалярным произведением векторов a(a1;a2;a3) и b(b1;b2;b3) в пространстве называется число a1b1 + a2b2 + a3b3: 1) a × a = a² = |a|²; 2) a × b = |a| × |b| cosφ; 3) a ⊥ b ⇔ a × b × 0 — условие перпендикулярности двух векторов. cosφ =
1) гой ответ. №4. Даны точки А(2;7;-3) и В 1) 4) №5. Даны точки А(3;-2;4),В(4;-1;2),С(6;-3;2),Д(7;-3;1).Найдите угол между векторами АВ и СД 1) 150°; 2) 30°; 3) 45°; 4) 60°; 5) 120°. №6. Зная, что 1) 12; 2) 18; 3) 20; 4) 25; 5) 30. №7. В параллелограмме АВСД заданы А(-5;2;8), Координатные векторы (орты) направлены вдоль осей координат. Модули этих векторов равны 1. e1(1;0;0), e2(0;1;0), e3(0;0;1).
Произвольный вектор a можно разложить единственным способом по координатным векторам. a(a1;a2;a3) = a1e1 + a2e2 + a3e3. Коэффициенты разложения ai являются проекциями вектора a на оси координат.
Разложение вектора в пространстве по трем некомпланарным векторам Компланарными называются векторы, параллельные одной и той же плоскости. m — произвольный вектор пространства, a, b и c — некомпланарные (то есть непараллельные одной плоскости) векторы. Всегда существует разложение: m = αa + βb + γc(α, β и γ — единственные)
|

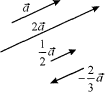
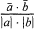


 (1;-2;1).Разложите вектор
(1;-2;1).Разложите вектор  по координатным векторам:
по координатным векторам: ; 2)
; 2) 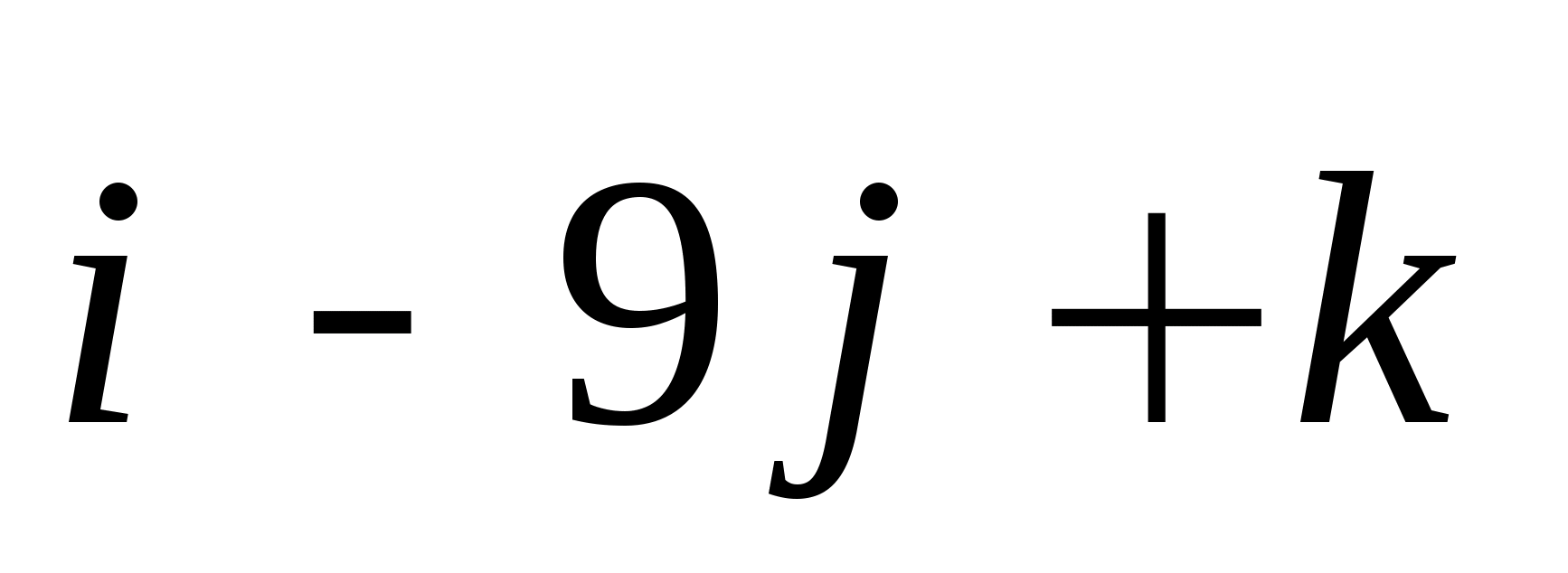 ; 3)
; 3)  ;
;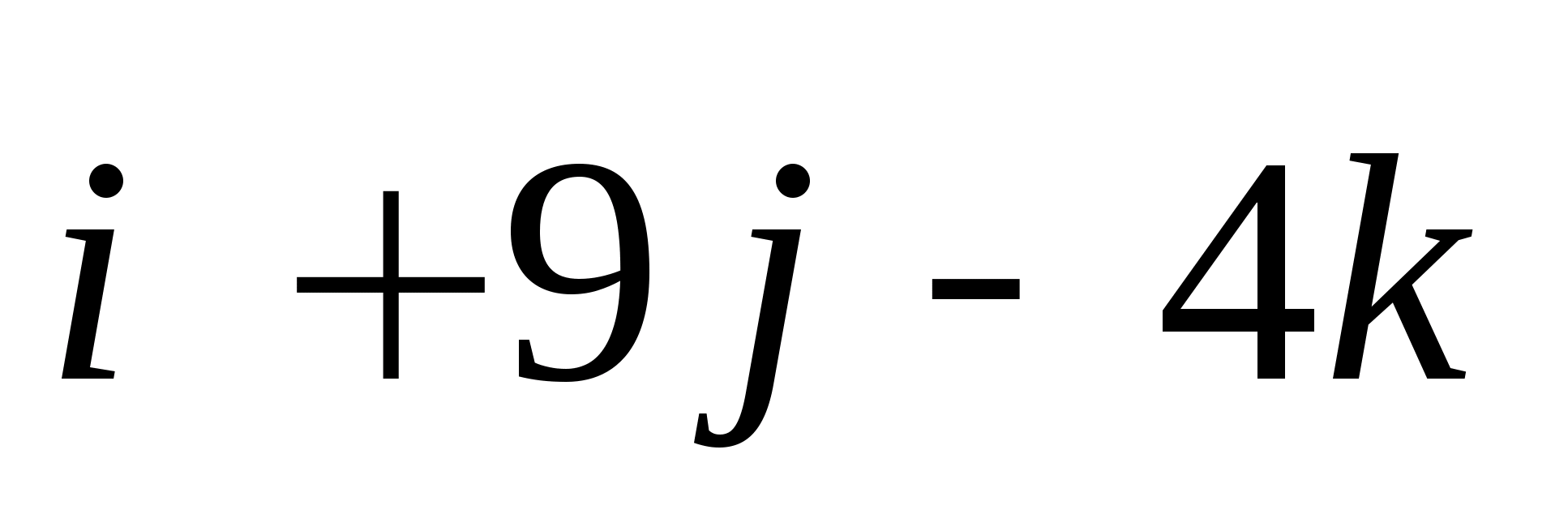 ; 5)
; 5)  .
.
 -2;4;6). Сумма координат точки Д равна Единичные векторы — это векторы, модули которых — единицы.
-2;4;6). Сумма координат точки Д равна Единичные векторы — это векторы, модули которых — единицы.





