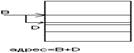
Частные случаи реш-я з распозн-я тупика.

Осн недостаток этого подхода – необх-ть изменения графа ПИР при моделировании поведения сист. В реальных сист вып-е этих операций над графом – это вып-е операций над сист стр-ми данных, предст-щих процессы и рес. А эти оп-ции должны вып-ся только тогда, когда изменяется состояние процессов и рес – вып-ся запросы, выделение, освоб-е. Нужно дублировать эти стр-ры данных – накл расходы. В реал сист рассм методы распознавания тупиков при некот ограничениях: 1)сист с единичными рес. В таких сист нал-е цикла в графе ПИР явл необх и дост усл-ем тупика; 2)сист с ограничениями на пор выд-я рес (запрещ асинхр работа). Наличие узла в графе ПИР, представл выгодное сост-е сист говорит о наличии тупика в этом сост (алг-м распозн-я узла: а.форм-ся мн-во из стоков; б. вкл-ся все верш, из к-рых достиж вершины того мн-ва – в цикле по всем верш. Оставшиеся принадл узлу). Если в сист вып-ся единич запросы на рес, то нал-е узла явл необх и дост усл-ем тупика; 3)сист с ПР. Общ метод – редукция графа ПР. Алг-м редукции: уничтожаем все дуги запросов; если процесс производит рес, то к пометкам этих рес прибавл величины запросов, а если потребитель – вычит. Теорема: Процесс в сист с ПР нах-ся в тупике в таком сост сист, если не сущ п-ти сокр-ний, в рез-те к-рой верш, предст процесс, стала бы изолир. Алг-м неэфф – нужен еще и перебор. 4)сист с обобщ рес.

Вывод сист из тупика. Осн методы: 1. Прекращение процессов, попавших в тупик; 2. Перераспределение рес (для ПИР).

Пор прекр-я процессов? Кр-рий – стоимость рестарта или возобновления его вып-я, играют роль вр работы и важность для сист. В 1-ю очередь прекр-ся процессы с мин стоимостью рестарта. Такое реш-е может оказ-ся неопт-ным – минимизируя стоимость на каждом шаге можем снять очень много пр-мм и суммарная стоимость будет высокой. Общий подход: все мн-во процессов разбивается на 2 п/мн-ва М1 и М2 таких, что если Ск – стоимость рестарта процесса Рк, то вып-ся усл-е: сумма(Ск, по всем из М1)<=сумма(Ск,по всем из М2). В М1 вкл те процессы, разрушение к-рых выводит сист из тупика с мин стоимостью. Если сист без огр-ний на выд-е и распр-е рес – это переборная задача. Вывод из тупика сист с огр-ми на запросы и пор распр-я рес (для сист, к-е поддерж-ся в выгодном сост с единич запросами на рес необ и дост усл-е тупика – нал-е узла. Т о чтобы вывести сист из тупика нужно разрушить все узлы в графе, предст тупиковое сост сист. Алг-м: 1. Обнаружить все узлы в графе ПИР, представл тупиковое сост сист; 2. По всем узлам: найти верш Rj, принадл узлу, такую, что сумма(Cij, по всем |(Pi,Rj)|>0)<=сумма(Cij, по всем |(Pi,Rk)|), Rk<>Rj, для к-рых их вершины входят в тот же узел. Превращаем верш Rj в сток – оставляем только дуги запросов. Удаляем дуги выд-я. Т о узел разрушен. В сист с един рес дост-но завершить один процесс – разрушить цикл.

З обхода тупиков (в сист тупики возм, это задача прогнозированиявозм-ти возникновения тупика и его предотвращения в том сл-е, когда вер-ть его возникновения велика). Алг-м основан на прогноз-нии поведения сист при самых неблагопр усл-ях. Сист должна поддерживать себя при вып-нии оп-ций всегда в безопасном сост. При выделении рес в ответ на запрос сист должна спрогноз-ть самые плохие последствия вып-я этой оп-ции. Для такого прогн-я необх строить граф макс потребностей. При порождении процесса сист должна получить инф-ю о макс потр-тях этого проц в рес. Граф макс потр-тей – это граф ПИР, в к-ром достраиваются дуги от проц к рес такие, что вес этих дуг Nij=Cij-(|(Rj,Pi)|+|(Pi,Rj)|), от Pi к Rj. Оп-ция выд-я рес вып-ся только тогда, когда граф макс потр-тей, полученный после вып-я этой о-ции, останется полностью сокр-мым (т е безопасн сост, это был алг-м банкира). Для ПР з обхода тупика можно решить только при огр-ниях. Сист должна знать не только произв-лей, но и всех потреб-лей этих рес. 1) мн-во процессов = мн-во произв-лей + мн-во отреб-лей; 2)сост-е сист представл-ся графом с огр-ми на требования. В этом графе проц запрашивает ед-цу рес, т е сущ дуга от проц к рес весом 1 <=> когда проц явл потреб-лем этого рес; 3)По всем ПР кол-во своб ед-ц = 0. Если такой граф будет сокр-мым, то сист будет выделять рес.

Управление памятью.

память – это осн рес, по структуре – составной, посл-но исп-мый, виртуализируемый.

Стат и дин распр-е пам.

Пам распр-ся стат-ки, если объем пам, исп-мой пр-ммой, опр-ся до начала вып-я пр-ммы – либо во вр трансляции, либо во вр компоновки опр-ся общий объем памяти и то, как она будет распред-ся. При дин-ком распр-нии пам она выд-ся во вр вып-я пр-ммы. Выделять пам дин-ки можно автом-ки, либо по запросу пргр-та (new, из кучи). Автом-ки – под процедуры, лок данные проц-р и ф-ий при их вызове, для передаваемых пар-ров а также для хранения служеб инф-ции и временных рабочих пер-ных, данных. Служебные данные – регистр флагов, точка возврата. Структура – стек. Сущ сист прогр-я, где не исп-ся дин распр-е пам – невозм рекурсия, дин стр-ры данных. Такой способ распред-я пам реализ-ся в сист, в к-рых реал-ся работа с большими вычислениями, где треб-ся большая скорость (фортран), исп-ся итерация вместо рекурсии. Пам исп-ся неэф, но быстро. Пам может выд-ся разрывными или непр блоками. Истор-ки 1-й способ – связными обл-ми. Т е пам для всей пр-ммы выд-ся одним блоком. При таком способе орг-ции легче орг-ть защиту. Нужно знать нач и конец блока – легко проверить, в свой ли блок обращается пр-мма (ошибки адресации). Алг-мы распред-я пам упрощаются. Недостаток – неэф исп-ние пам. Для повыш-я эф-ти исп-ния пам стали исп-ть перемещаемые разделы, границы к-рых можно было изменять. При реал-ции перемещаемых разделов возникла проблема перенастройки ссылок при кажд перемещении раздела. Это можно было реал-ть только на основе относит адресации. При относит адресации пам адрес сост как мин из 2-х компонент – адрес блока и см внутри блока.

Такой способ адр-ции потребовал появления спец адресных регистров. Разделение ф-ий регистров на адресные, арифм, системные может привести к их неэф исп-нию. Если не делить рег-ры на адр и арифм (не трогать сист) – рег общ назначения. Такое исп-ние рег-ров усложняет настройку при дин распр-нии пам или при перемещении блоков. Для реш-я проблем, связ с настройкой адресов при перемещении блоков реал-ся слож алг-мы, накл расходы. Одним из вар-тов реш-я проблемы стал отказ от перемещения блоков, замена на возм-ть разрывного распред-я пам для пр-ммы.

Сущ 3 осн способа разрывных распределений пам – сегм, стр и сегм-стр орг-ции.