Углы Крылова
Воспитатель вместе с детьми заучивает ритмодекламацию. Дети делятся на две команды и по очереди произносят слова с каждым разом все быстрее и быстрее. Произносить надо четко. Воспитатель определяет победителя. Кот мяучит, собака лает. Собака лает, рыба молчит. Кот мяучит, собака лает. Собака лает, змея шипит. Кот мяучит, собака лает. Собака лает, утка кричит. Кот мяучит, собака лает.Собака лает, облако летит. Кот мяучит, собака лает. Собака лает, пчела жужжит, (лошадка бежит, мышь пищит и т.д.). Углы Крылова угол дифферента угол крена угол рыскания Переход от осей неподвижной системы координат CXYZ к системе Cxyz, неизменно связанной с кораблем, выполняется с помощью трех поворотов:
1 ) поворот системы CXYZ вокруг третьей из координатных осей CZ= Cz 1 на угол дифферента
Формулы преобразования координат связаны следующими соотношениями в матричной форме: от CXYZ Þ к или где
2) поворот системы
Формулы преобразования координат связаны следующими соотношениями в матричной форме: от системы [ x 1] =
3) поворот системы
Формулы преобразования координат связаны следующими соотношениями в матричной форме: от системы координат или где поворотная матрица {a2j }т – это матрица, транспонированная к матрице { a2j }, имеет вид
Подставляя в (1) соотношения (3) и (5), получаем:
Где матрица
=
|

 , (килевая качка)
, (килевая качка) , (бортовая качка)
, (бортовая качка)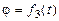 .
.
 , в результате чего получим систему Cx 1 y 1 z 1.
, в результате чего получим систему Cx 1 y 1 z 1.
 [ X ] ={ a3y}т [ x 1],
[ X ] ={ a3y}т [ x 1], (1),
(1), - поворотная матрица, транспонированная к матрице
- поворотная матрица, транспонированная к матрице  ,
, . (2).
. (2). вокруг первой из координатных осей
вокруг первой из координатных осей  на угол крена
на угол крена 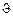 , в результате чего получим систему
, в результате чего получим систему  , при этом
, при этом 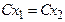 .
.

 [ x 2], или
[ x 2], или  (3), где
(3), где  ,
, . (4)
. (4) на угол рыскания
на угол рыскания  , в результате чего приходим к системе Cxyz, при этом.
, в результате чего приходим к системе Cxyz, при этом.  =
= 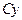 .
.
 [ x ],
[ x ], ,(5)
,(5) (6). (6)
(6). (6) или
или 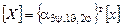 или
или  , (7)
, (7) транспонирована к матрице направляющих косинусов
транспонирована к матрице направляющих косинусов  , является произведением трех поворотных матриц
, является произведением трех поворотных матриц
 =
=


 .(8)
.(8)


