Уравнение линейной множественной регрессии. Оценка параметров множественной регрессии
Экономические явления, как правило, определяются большим числом одновременно и совокупно действующих факторов. В связи с этим часто возникает задача исследования зависимости переменной у от нескольких объясняющих переменных (х1, х2,…, хk) которая может быть решена с помощью множественного корреляционно-регрессионного анализа. При исследовании зависимости методами множественной регрессии задача формируется так же, как и при использовании парной регрессии, т.е. требуется определить аналитическое выражение формы связи между результативным признаком у и факторными признаками х,, х2,..., хk, найти функцию Множественная регрессия широко используется в решении проблем спроса, доходности акций, при изучении функции издержек производства, в макроэкономических расчетах и целом ряде других вопросов эконометрики. В настоящее время множественная регрессия – один из наиболее распространенных методов в эконометрике. Основная цель множественной регрессии – построить модель с большим числом факторов, определив при этом влияние каждого из них в отдельности, а также совокупное их воздействие на моделируемый показатель. Из-за особенностей метода наименьших квадратов во множественной регрессии, как и в парной, применяются только линейные уравнения и уравнения, приводимые к линейному виду путем преобразования переменных. Чаще всего используется линейное уравнение, которое можно записать следующим образом:
a0, a1, …, ak – параметры модели (коэффициенты регрессии); εj – случайная величина (величина остатка). Коэффициент регрессии а jпоказывает, на какую величину в среднем изменится результативный признак у, если переменную х jувеличить на единицу измерения при фиксированном (постоянном) значении других факторов, входящих в уравнение регрессии. Параметры при x называются коэффициентами «чистой» регрессии. Пример. Предположим, что зависимость расходов на продукты питания по совокупности семей характеризуется следующим уравнением:
y – расходы семьи за месяц на продукты питания, тыс. руб.; x 1 – месячный доход на одного члена семьи, тыс. руб.; x 2 – размер семьи, человек. Анализ данного уравнения позволяет сделать выводы – с ростом дохода на одного члена семьи на 1 тыс. руб. расходы на питание возрастут в среднем на 350 руб. при том же среднем размере семьи. Иными словами, 35% дополнительных семейных расходов тратится на питание. Увеличение размера семьи при тех же ее доходах предполагает дополнительный рост расходов на питание на 730 руб. Первый параметр не подлежит экономической интерпретации. Оценивание достоверности каждого из параметров модели осуществляется при помощи t-критерия Стьюдента. Для любого из параметров модели аjзначение t-критерия рассчитывается по формуле Sε – стандартное (среднее квадратическое) отклонение уравнения регрессии) определяется по формуле
Коэффициент регрессии аjсчитается достаточно надежным, если расчетное значение t- критерия с (n — k — 1) степенями свободы превышает табличное, т.е. tрасч > t а jn-k-1. Если надежность коэффициента регрессии не подтверждается, то следует; вывод о несущественности в модели факторного j признака и необходимости его устранения из модели или замены на другой факторный признак. Важную роль при оценке влияния факторов играют коэффициенты регрессионной модели. Однако непосредственно с их помощью нельзя сопоставлять факторные признаки по степени их влияния на зависимую переменную из-за различия единиц измерения и разной степени колеблемости. Для устранения таких различий применяются частные коэффициенты эластичности Эj и бета-коэффициенты βj. Формула для расчета коэффициента эластичности
aj – коэффициент регрессии фактора j,
Коэффициент эластичности показывает, на сколько процентов изменяется зависимая переменная у при изменении фактора j на 1 %. Формула определения бета - коэффициента.
Sxj – среднее квадратическое отклонение фактора j; Sy - среднее квадратическое отклонение фактора y. β - коэффициент показывает, на какую часть величины среднего квадратического отклонения Sy изменится зависимая переменная у с изменением соответствующей независимой переменной х jна величину своего среднего квадратического отклонения при фиксированном значении остальных независимых переменных. Долю влияния определенного фактора в суммарном влиянии всех факторов можно оценить по величине дельта-коэффициентов Δj. Указанные коэффициенты позволяют проранжировать факторы по степени влияния факторов на зависимую переменную. Формула определения дельта - коэффициента.
ryj – коэффициент парной корреляции между фактором j и зависимой переменной; R2 – множественный коэффициент детерминации. Коэффициент множественной детерминации используют для оценки качества множественных регрессионных моделей. Формула определения коэффициента множественной детерминации.
Коэффициент детерминации показывает долю вариации результативного признака, находящегося под воздействием факторных признаков, т.е. определяет, какая доля вариации признака у учтена в модели и обусловлена влиянием на него факторов, включенных в модель. Чем ближе R2 к единице, тем выше качество модели При добавлении независимых переменных значение R2 увеличивается, поэтому коэффициент R2 должен быть скорректирован с учетом числа независимых переменных по формуле
Для проверки значимости модели регрессии используется F-критерий Фишера. Он определяется по формуле
Если расчетное значение критерия с γ1, = k и γ 2 = (n — k— 1) степенями свободы больше табличного при заданном уровне значимости, то модель считается значимой. В качестве меры точностимодели применяют стандартную ошибку, которая представляет собой отношение суммы квадратов уровней остаточной компоненты к величине (n — k —1):
Классический подход к оцениванию параметров линейной модели основан на методе наименьших квадратов (МНК). Система нормальных уравнений имеет вид:
Решение системы может быть осуществлено по одному из известных способов: Метод Гаусса, метод Крамера и т.д. Пример15. По четырем предприятиям региона (таблица 41) изучается зависимость выработки продукции на одного работника y (тыс. руб.) от ввода в действие новых основных фондов Таблица 41 – Зависимость выработки продукции на одного работника
Решение: Предположим, что зависимость выработки продукции на одного работника характеризуется следующим уравнением:
На основании исходных данных составляем систему уравнений для определения коэффициентов
Решим эту систему по методу Крамера. Вычисляем определитель системы:
Аналогично вычисляем частные определители, заменяя соответствующий столбец столбцом свободных членов:
Коэффициенты уравнения определяются по формулам:
Таким образом, уравнение имеет вид:
Для определения параметров множественной регрессии на основе матрицы парных коэффициентов корреляции строится уравнение регрессии в стандартизованном масштабе:
где
Применяя МНК к уравнению множественной регрессии в стандартизованном масштабе, после соответствующих преобразований получим систему нормальных уравнений вида для определения стандартизованных коэффициентов регрессии.
Величины
Решая систему уравнений, определяют стандартизованные коэффициенты регрессии. Сравнивая их друг с другом, можно ранжировать факторы по силе воздействия на результат. В этом основное достоинство стандартизованных коэффициентов регрессии в отличие от коэффициентов «чистой» регрессии, которые несравнимы между собой. Пример16: Продолжение примера 15. Получим уравнение регрессии в стандартизованном масштабе (таблица 42). Таблица 42 – Уравнение регрессии в стандартизованном масштабе.
Получаем систему нормальных уравнений в виде:
Окончательно получаем уравнение регрессии в стандартизованном масштабе в виде:
Используя формулы
Сравнивая уравнение с полученным уравнением в примере 15, можно увидеть соответствие результатов в построении уравнения множественной регрессии полученных разными способами.
|

 , где k – число факторных признаков
, где k – число факторных признаков , где
, где ,где
,где , где
, где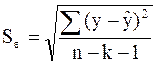
 где
где - среднее значение результативного признака
- среднее значение результативного признака - среднее значение признака j
- среднее значение признака j , где
, где , где
, где




 (% от стоимости фондов на конец года) и от удельного веса рабочих высокой квалификации в общей численности рабочих
(% от стоимости фондов на конец года) и от удельного веса рабочих высокой квалификации в общей численности рабочих  (%). Требуется написать уравнение множественной регрессии.
(%). Требуется написать уравнение множественной регрессии. , (тыс. руб.)
, (тыс. руб.)
 .
. и
и  .
. ;
; ;
;  ;
; ;
; ;
; ;
;  ;
; .
.

 ;
;  ;
;  .
.
 .
. ,
, - стандартизованные переменные:
- стандартизованные переменные: , для которых среднее значение равно нулю, а среднее квадратическое значение равно единице;
, для которых среднее значение равно нулю, а среднее квадратическое значение равно единице;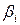 - стандартизованные коэффициенты регрессии.
- стандартизованные коэффициенты регрессии. .
. и
и 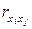 называются парными коэффициентами корреляции и определяются по формулам
называются парными коэффициентами корреляции и определяются по формулам ,
,  .
.
 ,
,  ,
,  ,
, 
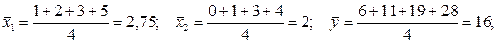







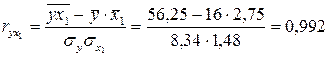 ;
; ;
; .
.

 можно вернуться к уравнению «чистой» регрессии:
можно вернуться к уравнению «чистой» регрессии: 





