Коэффициент корреляции
Теснота связи количественно выражается величиной коэффициентов корреляции. Построение коэффициентов корреляции основано на сумме произведений отклонений индивидуальных значений признаков х и у от их средних значений
где n — объем исследуемой совокупности; x1 - i-е значение независимой переменной (i = I, 2,.... n); у1- 1-е значение зависимой переменной (i = 1.2.....и);
Размер ковариации зависит от масштаба признаков х и y. Для получения относительной характеристики связи ковариацию делят на максимально возможное значение, равное произведению средних квадратических отклонений двух признаков σх, σy. В результате получают линейный (парный) коэффициент корреляции.
где σх, σy – среднеквадратические отклонения случайных величин х и y, определяется по формулам
Коэффициент корреляции принимает значение от -1 до +1. Положительное значение коэффициента свидетельствует о наличии прямой связи, отрицательное значение — обратной. Если rух = ±1, корреляционная связь представляется линейной функциональной зависимостью. При rух = 0 линейная корреляционная связь отсутствует. Качественные характеристики связи представлены в таблице 34 Таблица 34 – Качественные характеристики связи.
Коэффициенты корреляции как статистические величины подвергаются в анализе оценке на достоверность. Это объясняется тем, что любая совокупность наблюдений представляет собой некоторую выборку, следовательно, значение любого показателя, вычисленное на основе выборки, не может рассматриваться как истинное, а является только более или менее точной его оценкой. В связи с этим возникает необходимость проверки существенности (значимости) показателей. Для оценки значимостикоэффициента корреляции используют t -критерий Стьюдента ( t -статистику), который применяется при t -распределении, отличном от нормального. При этом выдвигается и проверяется нулевая гипотеза (H0 |) о равенстве rух нулю. Если нулевая гипотеза отвергается, то коэффициент корреляции признается значимым, а связь между переменными существенной. Формула расчета t -критерия Стьюдента
где k – число факторных признаков, включенных в модель. Значение t –критерия сравнивают с табличным t αγ , где α – заданный уровень значимости (обычно принимается равным 0,05 или 0,01); γ - =(n – k -1) - число степеней свободы. Если выполняется неравенство t > t αγ, то значение коэффициента корреляции признается значимым, т.е. нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается и делается вывод о том, что между исследуемыми переменными есть тесная статистическая взаимосвязь. Зная линейный коэффициент корреляции, можно определить парный коэффициент детерминации, он представляет собой rух. Парный коэффициент детерминациипоказывает, какая доля вариации переменной у учтена в модели и обусловлена влиянием на нее переменной x.
|

 и
и  :
:  . Деление данной величины на число единиц совокупности n, называется ковариацией. Ковариация характеризует сопряженность вариации двух признаков и представляет собой статистическую меру взаимодействия двух случайных переменных.
. Деление данной величины на число единиц совокупности n, называется ковариацией. Ковариация характеризует сопряженность вариации двух признаков и представляет собой статистическую меру взаимодействия двух случайных переменных.
 - среднее значение независимой переменной. Определяется по формуле
- среднее значение независимой переменной. Определяется по формуле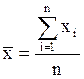



 .
.



