Расчет доверительных интервалов прогноза
Прогнозные значения исследуемого показателя определяют путем подстановки в уравнение кривой времени t, соответствующей периоду упреждения. Полученный прогноз называют точечным. В дополнение к точечному прогнозу можно определить границы возможного изменения прогнозируемого показателя, т. е. вычислить интервальный прогноз. Если тренд характеризуется прямой или полиномом второго порядка, то доверительный интервал можно представить в виде п — длина временного ряда; L — период упреждения;
Sy2 — дисперсия отклонений фактических наблюдений от расчетных:
уt — фактическое значение уровней ряда;
k — число оцениваемых параметров выравнивающей кривой (для прямой k = 2, для параболы 2-й степени k = 3 и т. д.). Значения К* в зависимости от длины временного ряда и периода упреждения для прямой и параболы представлены в таблице 30 при доверительной вероятности 0,9. Таблица 30 – Значения К* в зависимости от длины временного ряда и периода упреждения для прямой и параболы
Пример 11. По статистическим данным о производстве угля за 9 лет (2000-2008 гг.) были рассчитаны параметры модели Решение: Определим точечный прогноз:
Интервальный прогноз. По данным задачи n = 9, L = 1, линейный тренд по табл. К* = 2,3422:
Точечный прогноз равен 276 млн. т. Нижняя граница прогноза составляет 276 - 6.98 = 269.02 млн. т. Верхняя граница прогноза равна 276 + 6.98 = 282.98 млн. т.
|




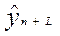 — точечный прогноз на момент п + L;
— точечный прогноз на момент п + L;
 — расчетные значения уровней ряда;
— расчетные значения уровней ряда; и дисперсия отклонений фактических значений от расчетных Sy2 = 8,9 (млн. т.)2. Используя полученную модель, рассчитать интервальный прогноз производства в 2009 г. доверительную вероятность принять равной 0,9. Найти нижнюю и верхнюю границы прогноза.
и дисперсия отклонений фактических значений от расчетных Sy2 = 8,9 (млн. т.)2. Используя полученную модель, рассчитать интервальный прогноз производства в 2009 г. доверительную вероятность принять равной 0,9. Найти нижнюю и верхнюю границы прогноза.





