Применение моделей кривых роста в прогнозировании временных рядов
Комплекс аналитических методов выравнивания сводится к выбору конкретных кривых роста и определению их параметров. Под кривой роста понимают функцию, аппроксимирующую заданный динамический ряд. Разработка прогноза с использованием кривых роста включает следующие этапы: 1. выбор одной или нескольких кривых, форма которых соответствует динамике временного ряда; 2. оценка параметров выбранных кривых; 3. проверка адекватности выбранных кривых прогнозируемому процессу и окончательный выбор кривой; 4. расчет точечного и интервального прогнозов. Кривые роста обычно выбираются из трех классов функций. К первому классу относятся кривые, которые используются для описания процессов с монотонным характером развития и отсутствием пределов роста. Ко второму классу относятся кривые, имеющие предел роста в исследуемом периоде. Такие кривые называют кривыми насыщения. Если кривые насыщения имеют точки перегиба, то они относятся к кривым третьего класса. Их называют S - образными кривыми. Среди кривых роста первого типа выделяют класс полиномов: уt = а0 + а1t + а2t2 + а3t3 +... Параметр а0 является начальным уровнем ряда при t = 0, а1 - линейныq прирост, а2 — ускорение роста, а3 — изменение ускорения роста. В эконометрических исследованиях в большинстве случаях применяются полиномы не выше третьего порядка. Уравнение линейного тренда ŷt = a0 + a1t ŷt - выровненные (теоретические) уровни тренда для лет с номером I, t – номера моментов или периодов времени, к которым относятся уровни временного ряда (год, месяц, др.) a0, a1 – параметры тренда. Характеристика параметров линейного тренда a0 - коэффициент тренда, численно равный среднему выровненному уровню для момента, или периода времени, принятого за начало отсчета (ti = 0); a1 - коэффициент тренда, характеризующий среднее и з менение уровней ряда за единицу времени Величина параметров a0 и a1, определяется по методу наименьших квадратов. Для этого строят систему нормальных уравнений. Система нормальных уравнений для линейного тренда
Для решения уравнения с двумя неизвестными начало отсчета времени переносят в середину ряда. При нумерации периодов времени точно от середины ряда половина номеров t будет отрицательными числами, а половина — положительными, т.е. • для четного числа членов t=..., -5. -3, -1, 1, 3, 5..., • для нечетного числа членов t:=..., -3, -2, -1, 0, 1, 2, 3... В этом случае система нормальных уравнений сокращается.
На графике линейный тренд изображается в виде прямой и используется для описания процессов, развивающихся равномерно во времени. Т.е. для отображения тенденции примерно равномерного изменения уровней: равных в среднем в среднем величин абсолютного прироста или абсолютного сокращения уровней за равные промежутки времени.
Уравнение параболического тренда ŷt = а0 + а1t + а2t2 Значения параметров параболы такие же, как и в уравнении прямой, кроме a1, а2 a0, - коэффициент тренда, численно равный среднему выровненному уровню для момента или периода времени, принятого за начало отсчета (ti = 0). a1 – коэффициент тренда, характеризующий средний за весь период среднегодовой прирост, который уже не является константой, а изменяется равномерно со средним ускорением, равным 2а2. а2 – главный параметр уравнения, константа, характеризующая ускорение. Система нормальных уравнений для параболического тренда
При переносе начала отсчета периодов (моментов) времени в середину ряда, суммы нечетных степеней номеров этих периодов Σt. и Σt 3 = 0. Следовательно, второе уравнение становится уравнением с одним неизвестным. Отсюда можно выразить параметр а1:
Сокращенная система уравнений для параболического тренда
Формулы вычисления коэффициентов параболического тренда
На графике параболический тренд изображается в виде параболы и применяется в тех случаях, когда процесс развивается равноускоренно. Т.е. для отражения тенденций динамики, для которых на некотором, обычно непродолжительном, этапе развития свойственно примерно постоянное ускорение абсолютных изменений уровней. Если a2 > 0, то ветви параболы направлены вверх, в случае а2 < 0 — вниз. Уравнение гиперболического тренда a0 - свободный член гиперболы, предел, к которому стремится уровень ряда a1 - основной параметр гиперболы: Ø если a1 > 0, то этот тренд выражает тенденцию замедляющегося снижения уровней и при t→∞, ŷt→ a0 Ø если параметр a1 < 0, то с возрастанием t, т.е. с течением времени, уровни тренда возрастают и стремятся к величине a0при t→ ∞ При расчете гиперболического тренда нельзя нумеровать периоды времени от середины ряда, так как значения 1/ t должны быть всегда положительными. Уравнение экспоненциального тренда k - постоянный темп изменения уровней (цепной). Ø Если k > 1, то имеется тренд с возрастающими уровнями, причем это возрастание не просто ускоренное, а с возрастающим ускорением и возрастающими производными более высоких порядков. Ø Если k < 1, то имеется тренд, выражающий тенденцию постоянного, но замедляющегося сокращения уровней, причем замедление непрерывно усиливается. Экстремума экспонента не имеет и при t→ ∞ стремится либо к ∞ при k > 1, либо к 0 при k < 1 a - свободный член экспоненты равен выровненному уровню, т. е. уровню тренда в момент или период, принятый за начало отсчета времени (при t= 0) Экспоненциальный тренд характерен процессам, развивающимся в среде, не создающим никаких ограничений для роста уровней. Следовательно, на практике такие явления встречаются только в ограниченном промежутке времени, поскольку любая среда рано или поздно создает ограничения. Уравнение логарифмического тренда Уравнение логарифмического тренда применяют в том случае, когда изучаемый процесс приводит к замедлению роста показателя, но при этом рост не прекращается, а стремится к какому-нибудь ограниченному пределу. В этом случае ни гиперболическая форма тренда, ни парабола с отрицательным ускорением не подходят. Логарифмы возрастают значительно медленнее, чем сами числа (номера периодов t), но рост логарифмов не ограничен. Подбирая начало отсчета периодов (моментов) времени, можно найти такую скорость снижения абсолютных изменений, которая наилучшим образом отвечает фактическому временному ряду. Логарифмический тренд обладает следующими свойствами: Ø Если a1 > 0, то уровни возрастают, но с замедлением, а если a1 < 0, то уровни тренда уменьшаются, тоже с замедлением. Ø Абсолютные изменения уровней по модулю всегда уменьшаются со временем Ø Величины ускорения абсолютных изменений имеют знак, противоположный знаку самих абсолютных изменений, а по модулю постепенно уменьшаются Ø Темпы изменения (цепные) постепенно приближаются к 100% при t→ ∞ Логарифмический тренд, как и гиперболический, отражает постепенно затухающий процесс изменений. Однако эти тренды имеют существенное различие. Затухание по гиперболе происходит быстро при приближении к конечному пределу, а при логарифмическом тренде затухающий процесс продолжается без ограничения гораздо медленнее. Уравнения логистического тренда
При разных значениях параметров логистического уравнения ( a0и a1,) будут получаться разные виды трендов. Ø При a1 > 0, a1 < 0 - с ростом номеров периодов времени tполучается логистическая тенденция роста уровней, причем если нужно начать рост почти от нулевой величины, то a0 должно быть равно примерно 10. Чем больше модуль a1, тем быстрее будут возрастать уровни. Ø При a0 < 0, a1 > 0 - логистический тренд со снижением уровней, причем если снижение должно начинаться почти от единицы, то a0должно быть примерно равно —10. Чем больше a1, тем быстрее будут снижаться уровни. Логистическая форма трендаиспользуется для описания процессов, при которых изучаемый показатель проходит полный цикл развития, начиная от нулевого уровня, сначала медленно, но с ускорением возрастая; затем ускорение становится нулевым в середине цикла, т.е. рост происходит по линейному тренду; далее, в завершающей части цикла, рост замедляется по гиперболе по мере приближения к предельному значению показателя. Если диапазон изменения уровней от 0 до 1, то уравнение логистического тренда имеет вид (1). Если диапазон изменения уровней ограничен не нулем, а любыми значениями, определяемыми в зависимости от существа задачи, обозначаемыми утах и уmin, то формула логистического тренда примет вид (2) Пример 6: По данным месячных выпусков продукции фирмы за 8 месяцев (таблица 19, гр.2,3) Таблица 19 – Динамика выпуска продукции.
Необходимо произвести расчет - коэффициентов a0 и a1 линейного тренда и прогноз на месяц вперед - коэффициентов параболического тренда a0,a1, a3 прогноз на месяц вперед Решение: Для расчета коэффициентов линейного и параболического трендов произведем необходимые вычисления и заполним таблицу 20. Вычислим коэффициенты линейного тренда
Таблица 20 – Расчетные показатели.
Таким образом, величина среднего уровня ряда при t=0 составляет 3079,25, среднемесячное уменьшение выпуска продукции составляет 48,01. Уравнение линейного тренда: Прогноз на 9й месяц составит: Вычисляем коэффициенты параболического тренда по формулам
Уравнение параболического тренда:
Прогноз на 9-й месяц
|


 . Если до переноса начало координат t равно 1,2,3..., то после переноса:
. Если до переноса начало координат t равно 1,2,3..., то после переноса: где
где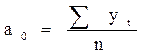 ;
; 









 (1)
(1) (2)
(2)





















