Автокорреляция, коэффициент автокорреляции.
При обработке временных рядов необходимо учитывать наличие автокорреляции и авторегрессии, при которых значения последующего уровня ряда зависят от предыдущих значений.
Автокорреляция – явление взаимосвязи между рядами: первоначальным и этим же рядом сдвинутым относительно первоначального положения на h моментов времени.
Авторегрессия – регрессия, учитывающая влияние предыдущих уровней ряда на последующие ряды.
Количественно автокорреляцию можно измерить с помощью линейного коэффициента корреляции между уровнями исходного временного ряда и уровнями этого ряда, сдвинутыми на несколько шагов во времени.
Формула для расчета коэффициента автокорреляции имеет вид:
 где где

Эту величину называют коэффициентом автокорреляции уровней ряда первого порядка, так как он измеряет зависимость между соседними уровнями ряда  и и  . .
Аналогично можно определить коэффициенты автокорреляции второго и более высоких порядков. Так, коэффициент автокорреляции второго порядка характеризует тесноту связи между уровнями  и и  и определяется по формуле: и определяется по формуле:
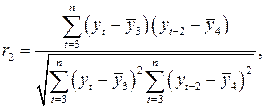 где где
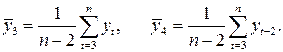
Сдвиг между соседними уровнями или сдвинутыми на любое число периодов времени называют временным лагом. С увеличением лага число пар значений, по которым рассчитывается коэффициент автокорреляции, уменьшается. Считается целесообразным для обеспечения статистической достоверности коэффициентов автокорреляции использовать правило – максимальный лаг должен быть не больше  . .
Свойства коэффициента автокорреляции.
1. Коэффициент корреляции строится по аналогии с линейным коэффициентом корреляции и таким образом характеризует тесноту только линейной связи текущего и предыдущего уровней ряда. Поэтому по коэффициенту автокорреляции можно судить о наличии линейной (или близкой к линейной) тенденции. Для некоторых временных рядов, имеющих сильную нелинейную тенденцию (например, параболу второго порядка или экспоненту), коэффициент автокорреляции уровней исходного ряда может приближаться к нулю.
2. По знаку коэффициента автокорреляции нельзя делать вывод о возрастающей или убывающей тенденции в уровнях ряда. Большинство временных рядов экономических данных содержат положительную автокорреляцию уровней, однако при этом могут иметь убывающую тенденцию.
Последовательность коэффициентов автокорреляции уровней первого, второго и т.д. порядков называют автокорреляционной функцией временного ряда. График зависимости ее значений от величины лага (порядка коэффициента автокорреляции) называется коррелограммой.
Анализ автокорреляционной функции и коррелограммы позволяет определить лаг, при котором автокорреляция наиболее высокая, а следовательно, и лаг, при котором связь между текущим и предыдущими уровнями ряда наиболее тесная, т.е. при помощи анализа автокорреляционной функции и коррелограммы можно выявить структуру ряда.
Если наиболее высоким оказался коэффициент автокорреляции первого порядка, исследуемый ряд содержит только тенденцию. Если наиболее высоким оказался коэффициент автокорреляции порядка  , то ряд содержит циклические колебания с периодичностью в , то ряд содержит циклические колебания с периодичностью в  моментов времени. Если ни один из коэффициентов автокорреляции не является значимым, можно сделать одно из двух предположений относительно структуры этого ряда: либо ряд не содержит тенденции и циклических колебаний, либо ряд содержит сильную нелинейную тенденцию, для выявления которой нужно провести дополнительный анализ. Поэтому коэффициент автокорреляции уровней и автокорреляционную функцию целесообразно использовать для выявления во временном ряде наличия или отсутствия трендовой компоненты и циклической (сезонной) компоненты. моментов времени. Если ни один из коэффициентов автокорреляции не является значимым, можно сделать одно из двух предположений относительно структуры этого ряда: либо ряд не содержит тенденции и циклических колебаний, либо ряд содержит сильную нелинейную тенденцию, для выявления которой нужно провести дополнительный анализ. Поэтому коэффициент автокорреляции уровней и автокорреляционную функцию целесообразно использовать для выявления во временном ряде наличия или отсутствия трендовой компоненты и циклической (сезонной) компоненты.
Пример 3.
Пусть имеются некоторые условные данные (таблица 11) об общем количестве поступившей товарной продукции на склад предприятия.
Таблица 11 – Общее количество поступившей товарной продукции на склад.
| Год
| Квартал
| 
| Количество поступившей товарной продукции, 
| |
| I
|
|
| | II
|
|
| | III
|
|
| | IV
|
|
| |
| I
|
|
| | II
|
|
| | III
|
|
| | IV
|
|
| |
| I
|
|
| | II
|
|
| | III
|
|
| | IV
|
|
| |
| I
|
|
| | II
|
|
| | III
|
|
| | IV
|
|
| Построим поле корреляции (рисунок 4).
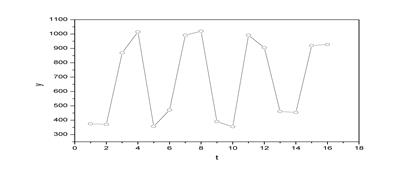
Рисунок 4 – Поле корреляции
Из графика видно, что значения  образуют пилообразную фигуру. Рассчитаем несколько последовательных коэффициентов автокорреляции. Для этого составляем первую вспомогательную таблицу (таблица 12). образуют пилообразную фигуру. Рассчитаем несколько последовательных коэффициентов автокорреляции. Для этого составляем первую вспомогательную таблицу (таблица 12).
Таблица 12 – Первая вспомогательная таблица.

| 
| 
| 
| 
| 
| 
| 
| |
|
|
|
|
|
|
|
| |
|
| –
| –
| –
| –
| –
| –
| |
|
|
| -328,33
| -288,13
| 94601,72
| 107800,59
| 83018,90
| |
|
|
| 169,67
| -292,13
| -49565,70
| 28787,91
| 85339,94
| |
|
|
| 315,67
| 205,87
| 64986,98
| 99647,55
| 42382,46
| |
|
|
| -342,33
| 351,87
| -120455,66
| 117189,83
| 123812,50
| |
|
|
| -228,33
| -306,13
| 69898,66
| 52134,59
| 93715,58
| |
|
|
| 292,67
| -192,13
| -56230,69
| 85655,73
| 36913,94
| |
|
|
| 320,67
| 328,87
| 105458,74
| 102829,25
| 108155,48
| |
|
|
| -309,33
| 356,87
| -110390,60
| 95685,05
| 127356,20
| |
|
|
| -344,33
| -273,13
| 94046,85
| 118563,15
| 74600,00
| |
|
|
| 292,67
| -308,13
| -90180,41
| 85655,73
| 94944,10
| |
|
|
| 205,67
| 328,87
| 67638,69
| 42300,15
| 108155,48
| |
|
|
| -238,33
| 241,87
| -57644,88
| 56801,19
| 58501,10
| |
|
|
| -245,33
| -202,13
| 49588,55
| 60186,81
| 40856,54
| |
|
|
| 220,67
| -209,13
| -46148,72
| 48695,25
| 43735,36
| |
|
|
| 227,67
| 256,87
| 58481,59
| 51833,63
| 65982,20
| | Сумма
|
|
| 9,05
| 0,05
| 74085,16
| 1153766,39
| 1187469,73
| | Среднее значение
| 699,33
| 663,13
| –
| –
| –
| –
| –
|
Вычисляем коэффициент автокорреляции первого порядка
 . .
Составляем вспомогательную таблицу для расчета коэффициента автокорреляции второго порядка (таблица 13).
Следовательно
 . .
Аналогично находим коэффициенты автокорреляции более высоких порядков, а все полученные значения заносим в сводную таблицу (таблица 14).
Анализ коррелограммы (рисунок 5) и графика исходных уровней временного ряда позволяет сделать вывод о наличии в изучаемом временном ряде сезонных колебаний периодичностью в четыре квартала.
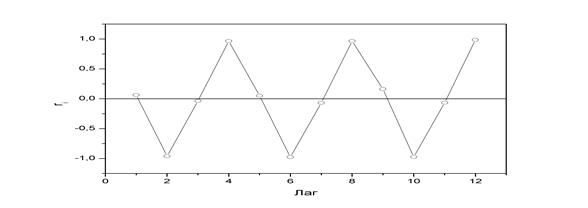
Рисунок 5 – Коррелограмма
Таблица 13 – Вспомогательная таблица.
| Лаг
| Коэффициент автокорреляции уровней
| |
| 0,063294
| |
| –0,961183
| |
| –0,036290
| |
| 0,964735
| |
| 0,050594
| |
| –0,976516
| |
| –0,069444
| |
| 0,964629
| |
| 0,162064
| |
| -0,972918
| |
| -0,065323
| |
| 0,985761
|
Таблица 14 – Сводная таблица расчетных показателей.

| 
| 
| 
| 
| 
| 
| 
| |
|
|
|
|
|
|
|
| |
|
| –
| –
| –
| –
| –
| –
| |
|
| –
| –
| –
| –
| –
| –
| |
|
|
| 145,57
| -269,79
| -39273,33
| 21190,62
| 72786,64
| |
|
|
| 291,57
| -273,79
| -79828,95
| 85013,06
| 74960,96
| |
|
|
| -366,43
| 224,21
| -82157,27
| 134270,94
| 50270,12
| |
|
|
| -252,43
| 370,21
| -93452,11
| 63720,90
| 137055,44
| |
|
|
| 268,57
| -287,79
| -77291,76
| 72129,84
| 82823,08
| |
|
|
| 296,57
| -173,79
| -51540,90
| 87953,76
| 30202,96
| |
|
|
| -333,43
| 347,21
| -115770,23
| 111175,56
| 120554,78
| |
|
|
| -368,43
| 375,21
| -138238,62
| 135740,66
| 140782,54
| |
|
|
| 268,57
| -254,79
| -68428,95
| 72129,84
| 64917,94
| |
|
|
| 181,57
| -289,79
| -52617,17
| 32967,66
| 83978,24
| |
|
|
| -262,43
| 347,21
| -91118,32
| 68869,50
| 120554,78
| |
|
|
| -269,43
| 260,21
| -70108,38
| 72592,52
| 67709,24
| |
|
|
| 196,57
| -183,79
| -36127,60
| 38639,76
| 33778,76
| |
|
|
| 203,57
| -190,79
| -38839,12
| 41440,74
| 36400,82
| | Сумма
|
|
| -0,02
| -0,06
| -1034792,71
| 1037835,43
| 1116776,36
| | Среднее значение
| 723,43
| 644,79
| –
| –
| –
| –
| –
|

Важнейшие способы обработки и анализа рядов динамики Не во всех случаях эмпирические данные рядов динамики позволяют определить тенденцию изменения явления во времени...
|

ТЕОРЕТИЧЕСКАЯ МЕХАНИКА Статика является частью теоретической механики, изучающей условия, при которых тело находится под действием заданной системы сил...
|

Теория усилителей. Схема Основная масса современных аналоговых и аналого-цифровых электронных устройств выполняется на специализированных микросхемах...
|

Логические цифровые микросхемы Более сложные элементы цифровой схемотехники (триггеры, мультиплексоры, декодеры и т.д.) не имеют...
|
Билиодигестивные анастомозы Показания для наложения билиодигестивных анастомозов:
1. нарушения проходимости терминального отдела холедоха при доброкачественной патологии (стенозы и стриктуры холедоха)
2. опухоли большого дуоденального сосочка...
Сосудистый шов (ручной Карреля, механический шов). Операции при ранениях крупных сосудов 1912 г., Каррель – впервые предложил методику сосудистого шва.
Сосудистый шов применяется для восстановления магистрального кровотока при лечении...
Трамадол (Маброн, Плазадол, Трамал, Трамалин) Групповая принадлежность
· Наркотический анальгетик со смешанным механизмом действия, агонист опиоидных рецепторов...
|
Травматическая окклюзия и ее клинические признаки При пародонтите и парадонтозе резистентность тканей пародонта падает...
Подкожное введение сывороток по методу Безредки. С целью предупреждения развития анафилактического шока и других аллергических реакций при введении иммунных сывороток используют метод Безредки для определения реакции больного на введение сыворотки...
Принципы и методы управления в таможенных органах Под принципами управления понимаются идеи, правила, основные положения и нормы поведения, которыми руководствуются общие, частные и организационно-технологические принципы...
|
|

 где
где
 и
и  .
. и
и  и определяется по формуле:
и определяется по формуле: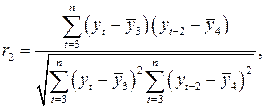 где
где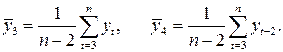
 .
. , то ряд содержит циклические колебания с периодичностью в
, то ряд содержит циклические колебания с периодичностью в 
 образуют пилообразную фигуру. Рассчитаем несколько последовательных коэффициентов автокорреляции. Для этого составляем первую вспомогательную таблицу (таблица 12).
образуют пилообразную фигуру. Рассчитаем несколько последовательных коэффициентов автокорреляции. Для этого составляем первую вспомогательную таблицу (таблица 12).







 .
. .
.









