Моделирование тенденции временного ряда.
Одним из наиболее распространенных способов моделирования тенденции временного ряда является построение аналитической функции, характеризующей зависимость уровней ряда от времени. Поскольку зависимость может принимать различные формы, то ее формализации можно использовать различные виды функций: линейную, гиперболическую, параболическую, степенную и т.п. Наиболее распространенным приемом для устранения аномальных значений показателей и отсутствия тенденции временного ряда является сглаживание временного ряда. При этом производится замена фактических уровней временного ряда расчетными данными, что способствует более четкому проявлению тенденции ряда. Скользящие средние позволяют сгладить случайные периодические колебания временного ряда. Сглаживание по простой скользящей средней Определяется интервал сглаживания (g). Для первых (g) уравнений временного ряда вычисляются их среднее. Длину интервала сглаживания (g) удобно брать в виде нечетного числа, в этом случае расчетное значение скользящей средней будет приходиться на средний интервал ряда. Формула расчета для интервала g =3
Сглаживание с использованием взвешенной скользящей средней. Применяют для рядов с нелинейной тенденцией развития. Уровни, входящие в интервал сглаживания суммируются с разными весами. Весовые коэффициенты при сглаживании по полиномам 2–го и 3-го порядков в зависимости от длины интервала сглаживания (таблица 15). Таблица 15 – Весовые коэффициенты при сглаживании по полиномам 2–го и 3-го порядков.
Для полиномов 2-го и 3-го порядков по 5 -членной взвешенной скользящей средней центральное значение интервала определяется по формуле: Пример 4: По данным динамики урожайности за 10 лет рассчитать (таблица 16) 3-,5- летние скользящие средние простые; 5-летние скользящие средние взвешенные. Сравнить результат расчетов.
Таблица 16 – Динамика урожайности за 10 лет.
Решение: 3-летние скользящие средние простые
5-летние скользящие средние простые
5-летние скользящие средние взвешенные
Вычисления заносим в таблицу 17. Таблица 17 – Показатели средних величин.
При сравнении значений yt 3- и 5-летних скользящих простых видно, что более гладкой является 5-летняя скользящая простая. При сравнении значений yt 5-летних скользящих простых и взвешенных видно, что более гладкой является 5-летняя скользящая простая, но скользящая взвешенная более близка к исходной.
|

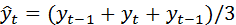

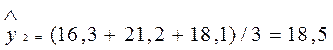
 т.д.
т.д.
 т.д.
т.д.
 т.д.
т.д.


