Расчет показателей динамики во временных рядах.
Для количественной оценки динамики экономических процессов применяют статистические показатели: абсолютные приросты, темпы роста и прироста. Они подразделяются на цепные, базисные и средние. Если сравнение уровней временного ряда осуществляется с одним и тем же уровнем, принятым за базу, то показатели называются базисными. Если сравнение осуществляется с переменной базой, каждый последующий уровень сравнивается с предыдущим, то вычисленные показатели называются цепными. Формулы для вычисления цепных, базисных и средних абсолютных приростов, темпов роста и темпов прироста даны в таблице 21. В формулах приняты обозначения: y1,y2,…,yt,…,yn— уровни временного ряда; п — длина ряда; yb — уровень временного ряда, принятый за базу сравнения. Описание динамики ряда средним приростом соответствует его представлению в виде прямой, проходящей через две крайние точки. Для получения прогнозного значения на один шаг вперед достаточно к последнему наблюдению добавить значение среднего абсолютного прироста: где
Таблица 21 – Формулы вычисления абсолютных приростов, темпов роста и темпов прироста.
Получение прогнозного значения по формуле корректно, если динамика ряда близка к линейной. На равномерный характер динамики указывают примерно одинаковые цепные абсолютные приросты. Использование среднего темпа роста (среднего темпа прироста) для описания динамики развития ряда соответствует его представлению в виде показательной или экспоненциальной кривой, проведенной через две крайние точки, и характерно для процессов, изменение динамики которых происходит с постоянным темпом роста. Прогнозное значение на i шагов вперед определяется по формуле где
Недостатком прогнозирования с использованием среднего прироста и среднего темпа роста является то, что они учитывают начальный и конечный уровни ряда, исключая влияния промежуточных уровней. Метод используются как простейший, приближенный способ прогнозирования. Пример 7. Ежеквартальная динамика фонда заработной платы работников фирмы в ден. ед. представлена в таблице 22. Обосновать правомерность использования среднего прироста для определения прогнозного значения фонда заработной платы в 6-м квартале. Таблица 22 – Ежеквартальная динамика фонда заработной платы.
Решение: Найдем цепные абсолютные приросты:
Цепные абсолютные приросты изменяются от 1 до 1,2, их изменения примерно одинаковы, что свидетельствует о близости ежеквартальной динамики фонда заработной платы фирмы к линейной. Поэтому правомерно определить прогнозное значение у6cпомощью среднего прироста
Пример 8. Изменение ежеквартальной динамики фонда заработной платы работников фирмы происходило примерно с постоянным темпом роста в течение 5 кварталов. Фонд заработной платы в 1-м квартале составлял 252 ден. ед., а в 5-м квартале — 256,5 ден. ед. Определить прогноз фонда заработной платы работников фирмы в 6-м квартале, используя средний темп роста. Решение: По условию, изменение фонда заработной платы происходило примерно с постоянным темпом роста в течение 5 кварталов. Поэтому правомерно использовать средний темп роста для расчета прогноза фонда в 6-м квартале. Средний темп роста составит:
Таким образом, прогноз величины фонда заработной платы сотрудников фирмы составит:
|

 — значение показателя в п точке временного ряда,
— значение показателя в п точке временного ряда,  — прогнозное значение показателя в точке п + 1,
— прогнозное значение показателя в точке п + 1,  — значение среднего прироста временного ряда.
— значение среднего прироста временного ряда.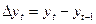





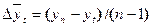



 — прогнозная оценка значения показателя в точке п + i,
— прогнозная оценка значения показателя в точке п + i, — средний темп роста, выраженный в относительных величинах.
— средний темп роста, выраженный в относительных величинах. = 253 - 252 = 1,
= 253 - 252 = 1, = 254,2 - 253 = 1,2,
= 254,2 - 253 = 1,2, = 255,3 - 254,2 = 1,1,
= 255,3 - 254,2 = 1,1, =256,5 - 255,3 = 1,2.
=256,5 - 255,3 = 1,2. :
: = (256,5 -252)/(5 -1) = 1,125,
= (256,5 -252)/(5 -1) = 1,125, =256,5 + 1,125 =257,625.
=256,5 + 1,125 =257,625.
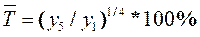 = (256,5/252)1/4 • 100 % = 100,44 %.
= (256,5/252)1/4 • 100 % = 100,44 %. = 256,5 *100,44 =257,6 ден. ед.
= 256,5 *100,44 =257,6 ден. ед.


