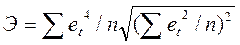Оценка адекватности модели

Независимо от вида выбранной модели вопрос о возможности ее применения для прогнозирования экономического показателя может быть решен только после установления ее адекватности. Проверка адекватности выбранных моделей реальному процессу строится на анализе случайного компонента. Случайный компонент получается после выделения из исследуемого ряда тренда и периодической составляющей. Если временной ряд не имеет сезонных колебаний, то для аддитивной модели

y_t = u_t + е_t ряд остатков может быть получен как отклонения фактических уровней у_t от расчетных ŷ: e_t=y_t- ŷ_t

При использовании кривых роста ŷ_t вычисляют, подставляя в уравнение кривой соответствующие значения времени.

Считается, что модель адекватна описываемому процессу, если значе­ния остаточного компонента удовлетворяют свойствам случайности, независимости и если распределены по нормальному закону распределения.

При правильном выборе вида тренда отклонения от него будут носить случайный характер и изменение остаточной случайной величины не будет связано с изменением времени. По выборке, полученной для всех временных значений на рассматриваемом интервале, проверяется гипотеза о независимости последовательности значений e_t, от времени или наличии тенденции в ее изменении. Для проверки этого свойства может быть использован критерий определения тенденции с помощью «восходящих» и «нисходящих» серий.

Если вид функции тренда выбран неудачно, то последовательные зна­чения остатков ряда могут не обладать свойствами независимости, так как могут коррелировать между собой. В этом случае говорят, что имеет место автокорреляция ошибок.

Наиболее распространенным приемом обнаружения автокорреляции является метод Дарвина — Уотсона, связанный с автокорреляцией между соседними остаточными членами ряда. Критерий Дарбина — Уотсона определяется по формуле d = ∑(e_t - e_t-1)²/∑e_t²

Применение критерия основано на сравнении величины d ≤ 2, рассчитанной по формуле, с теоретическими значениями d₁ и d₂, взятыми из таблицы 31, где приведены значения критерия Дарбина—Уотсона при доверительной вероятности 0,95.

Таблица 31 – Значения критерия Дарбина — Уотсона при доверительной вероятности 0,95

№	К'=1	К'= 2	К' = 3
d1	d2	d1	d2	d1	d2
	1,08	1,36	0,95	1,54	0,82	1,75
	1,13	1,38	1,02	1,54	0,9	1,71
	1,18	1,4	1,08	1,53	0,97	1,68
	1,22	1,42	1,13	1,54	1,03	1,67
	1,26	1,44	1,17	1,54	1,08	1,66
	1,29	1,45	1,21	1,55	1,12	1,66

 

Если в остатках имеется положительная автокорреляция, то при этом возможны три случая:

• если d < d₁ то гипотеза об отсутствии автокорреляции отвергается;

• если d > d₂, то гипотеза об отсутствии автокорреляции не отвергается;

• если d₁ < d < d₂, то нет достаточных оснований для принятия решений.

В том случае, когда расчетное значение критерия d > 2, то в е_t существует отрицательная автокорреляция и с значениями d₁ и d₂ сравнивается величина 4 - d.

В связи с тем, что временные ряды экономических показателей невелики, на основе анализа показателей асимметрии и эксцесса можно произвести проверку ряда остатков на нормальность распределения по формулам

где А — выборочная характеристика асимметрии, Э — выборочная характеристика эксцесса, σ_А — среднеквадратическая ошибка выбороч­ной характеристики асимметрии, σ_Э — среднеквадратическая ошибка выборочной характеристики эксцесса.

Если одновременно выполняются неравенства

|А| < 1,5σ_А; |э + 6/(n +1)| < 1,5σ_Э,

то гипотеза о нормальном характере распределения случайного ком­понента не отвергается. Если выполняется хотя бы одно из неравенств:

| А | > 2 σ_А; |Э + 6/(n+1)| >2 σ_Э,

то гипотеза о нормальном характере распределения отвергается.