Часть 1. В11.Найдите значение выражения
В11. Найдите значение выражения В12. Плотность N бактерий в биореакторе растет со временем по закону, В13. От треугольной пирамиды, объём которой равен 12, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объём отсеченной треугольной пирамиды.
В14. Из городов А и В навстречу друг другу выехали мотоциклист и велосипедист. Мотоциклист приехал в В на 3 часа раньше, чем велосипедист приехал в А, а встретились они через 48 минут после выезда. Сколько часов затратил на путь из В в А велосипедист? В15. Найдите точку минимума функции С1. а)Решите уравнение б) Найдите все корни этого уравнения, принадлежащие отрезку С2. Высота конуса равна 12, а радиус основания равен 10. Через вершину конуса и середину радиуса основания проведена хорда АВ окружности, перпендикулярная этому радиусу. Найдите площадь сечения конуса плоскостью, проходящей через хорду АВ и вершину конуса. С3. Решите систему неравенств: С4. В треугольнике АВС известно, что Продолжения высот треугольника АВС пересекают описанную около него окружность в точках М, N, Р. а) Докажите, что треугольник МNР прямоугольный. б) Найдите площадь треугольника МNР, если известно, что ВС = 12. С5. Найдите все значения параметра а, при каждом из которых уравнение С6. Все члены геометрической прогрессии – различные натуральные числа, заключённые между числами 510 и 740. а) Может ли такая прогрессия состоять из четырёх членов? б) Может ли такая прогрессия состоять из пяти членов?
Математика. 9 класс. Вариант 2 Часть 1 1 Найдите значение выражения 2 Фирма «Связь» выпустила в продажу две новые модели телефонов –
продавались в течение года. (По горизонтальной оси откладывается время, прошедшее с начала продаж – в месяцах, а по вертикальной — число телефонов, проданных за это время – в тыс. шт.).
На сколько телефонов модели А было продано больше, чем телефонов модели В за первые 8 месяцев года? Ответ дайте в тыс. штук. 3 Из объявления фирмы, проводящей обучающие семинары: «Стоимость участия в семинаре — 3000 р. с человека. Группам от организаций предоставляются скидки: от 5 до 10 человек — 5%; более 10 человек —8%». Сколько рублей должна заплатить организация, направившая на семинар группу из 8 человек? 4 На координатной прямой отмечено число a. Какому из отрезков принадлежит число a?
1) [−5; −4] 2) [−4; −3] 3) [−3; −2] 4) [3; 4] 5 Какому из данных выражений равно произведение
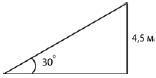
6 При проектировании торгового центра запланирована постройка эскалатора для подъёма на высоту 4,5 м под углом 300 к горизонту. Найдите длину эскалатора (в метрах).
8 Окружность с центром O касается сторон угла с вершиной A в точках B и C. Найдите Ð BAC, если Ð BOC =127°. Ответ дайте в градусах. Единицы измерения в ответе не указывайте. 9 Площадь любого выпуклого четырехугольника можно вычислять по формуле ними. Вычислите sin α;, если S = 21, d 1 = 7, d 2 = 15.
10 На диаграмме показано содержание питательных веществ в фасоли. Определите по диаграмме, содержание каких веществ превосходит 50%. (* – к прочему относятся вода, витамины и минеральные вещества.)
1) Белки
2) Жиры
3) Углеводы
4) Прочее
11 В таблице представлены результаты четырёх стрелков, показанные ими на тренировке. Тренер решил послать на соревнования того стрелка, у которого относительная частота попаданий выше. Кого из стрелков выберет тренер? В ответе укажите номер спортсмена.
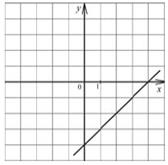
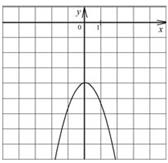
12 Для каждой функции, заданной формулой, укажите её график. А) y = 2 x2 − 4 Б) y = x − 4 В) y = x + 4
13 Путь от посёлка до железнодорожной станции пешеход прошёл за 3 ч, а велосипедист проехал за 1,2 ч. С какой скоростью (в км/ч) ехал велосипедист,
скорости пешехода? 14 Из прямоугольника со сторонами 5 см и 7 см вырезали квадрат со стороной 3 см. Найдите площадь оставшейся фигуры. Ответ дайте в см2. 15 Укажите в ответе номера верных утверждений. 1) Если в четырёхугольнике диагонали перпендикулярны, то этот четырёхугольник – ромб. 2) Если при пересечении двух прямых третьей накрест лежащие углы равны, то прямые параллельны. 3) Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и углу другого прямоугольного треугольника, то такие треугольники равны. 4) Если расстояние между центрами двух окружностей меньше суммы их радиусов, то эти окружности касаются.
окружность. 16 Окружность, изображённая на рисунке, задаётся уравнением уравнением y = −2 x. Вычислите координаты точки A. 17 Упростите выражение найдите его значение при
18 Решите неравенство 5 x − 2(4 − 2 x) > 4 x + 9.
|


 где N0 – начальная плотность бактерий, Т – период удвоения бактерий, t – время. Каким может быть наибольший период удвоения бактерий (в минутах), чтобы их конечная плотность достигла или превысила значение
где N0 – начальная плотность бактерий, Т – период удвоения бактерий, t – время. Каким может быть наибольший период удвоения бактерий (в минутах), чтобы их конечная плотность достигла или превысила значение  бактерий/мл за 10 часов работы в биореакторе? Начальная плотность бактерий составляет
бактерий/мл за 10 часов работы в биореакторе? Начальная плотность бактерий составляет  бактерий/мл.
бактерий/мл.





 имеет ровно три корня.
имеет ровно три корня.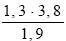
 модель А и модель В. На графиках показано, как эти модели
модель А и модель В. На графиках показано, как эти модели
 ?
? 1)
1)  2)
2)  3)
3)  4)
4) 
 7 Решите уравнение
7 Решите уравнение 
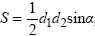 , где d 1, d 2 - длины его диагоналей, а α; угол между
, где d 1, d 2 - длины его диагоналей, а α; угол между

 1)
1)

 если его скорость на 9 км/ч больше
если его скорость на 9 км/ч больше 5) В любую трапецию можно вписать
5) В любую трапецию можно вписать , а прямая
, а прямая и
и



