Родственники

 

В методе Кранка-Николсона экспоненциал матрицы и интеграл аппроксимируются с большей точностью, чем в методе Эйлера:

Подставляя данные выражения в уравнение, получим:

 

 

Умножая слева на получаем:

 

Выражение в правой части считается явно, чтобы найти v(t+dt) нужно дважды решить систему линейных алгебраических уравненений. Это делается методом прогонки.

 

Исходный код программы:

 

#include<iostream>

#include<math.h>

#include<cstdlib>

#include<cstdio>

 

using namespace std;

 

#define sqr(x) ((x) * (x))

 

const int Nx = 40;

const double Nt = 6000;

 

 

double alpha, beta; double dx;

 

double a [Nx], b [Nx], c[Nx];

 

//Умножение вектора u на матрицу (E + lambda*A):

void matrix(double *u, double lambda) {

 

double dx = 1 / double(Nx);

double alpha = -1.0;

double beta = -2.0 + (1 - dx / 2) / (1 + dx / 2);

 

double v [Nx];

for (int i=1; i<Nx-1; i++) {

v[i] = u[i] + lambda * (u[i - 1] - 2.0 * u[i] + u[i + 1]) /sqr(dx) * D;

 

}

v[0] = u[0] + lambda * (beta * u[0] - u[1]) /sqr (dx) * D;

v[Nx - 1] = u[Nx - 1] + lambda * (u[Nx - 2] + u[Nx - 1] * alpha) /sqr (dx) * D;

 

for (int i = 0; i < Nx; i++) u[i] = v[i];

}

 

//Метод прогонки:

void sweep(double *u) {

for (int j = 0; j < Nx - 1; j++){

 

double w = b[j] / a[j];

a[j + 1] -= c[j] * w;

u[j + 1] -= u[j] * w;

}

for (int j = Nx - 1; j > 0; j--) {

double w = c[j - 1] / a[j];

u[j - 1] -= u[j] * w;

u[j] /= a[j];

}

u[0] /= a[0];

}

 

 

int main() {

 

double l=1, tau=1;

double xx = 2 * l / 3.0;

double tt = 5 * tau; //момент выхода из цикла по t

double dx = 1 / double(Nx);

double dt = tau / Nt;

double alpha = -1.0;

double beta = -2.0 + (1 - dx / 2) / (1 + dx / 2);

double D = sqr(l) / tau;

 

double u[Nx];

 

 

//задание начальных условий:

for (int i = 0; i < Nx; i++) {

u[i] = fabs((i + 0.5) * dx - (2*l/3.0)) < l / 10.0? 1.0: 0.0;

}

 

freopen("krahk_nicholson_t", "w", stdout);

 

int Ntt = tt / dt;

 

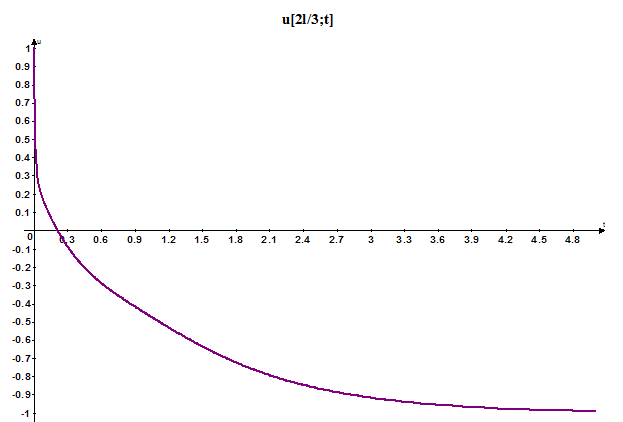
//Вычисление u в точке 2*l/3:

for (int i = 0; i < Ntt; i++) {

if (i < Nt)

cout << dt * i << " " <<

u[(int) (xx / l * double(Nx))] - (1 - exp(-i * dt / tau))<< '\n';

 

 

double q = 1.0 / tau * exp(-1 * i * dt / tau); //источник тепла в уравнении

double qq = exp(-1 * dt / tau);

 

 

//Вычисление правой части основной формулы:

double v[Nx], w[Nx], p[Nx];

for (int j = 0; j < Nx; j++) v[j] = u[j]; //v(t)

matrix(v, dt / 2);

matrix(v, dt / 2);

 

for (int j = 0; j < Nx; j++) w[j] = qq * q * dt / 2.0; //q(t+dt)

matrix(w, -dt / 2);

matrix(w, -dt / 2);

 

for (int j = 0; j < Nx; j++) p[j] = q * dt / 2.0; //q(t)

matrix(p, -dt / 2);

matrix(p, dt / 2);

 

 

for (int j = 0; j < Nx; j++) v[j] += w[j] + p[j];

 

//вычисление коэффициентов трехдиагональной матрицы:

for (int j = 0; j < Nx - 1; j++) {

a[j] = 1.0 + dt / sqr(dx) * D; b [ j ] = c [j] = -dt / sqr(dx) / 2 * D;

}

a[0] = 1 - dt * beta / 2 / sqr(dx) * D;

a[Nx - 1] = 1 - dt * alpha / 2 / sqr(dx) * D;

 

sweep(v);

 

//вычисление коэффициентов трехдиагональной матрицы:

for (int j = 0; j < Nx - 1; j++) {

a[j] = 1.0 - dt / sqr(dx) * D; b [j] = c [j] = +dt / sqr(dx) / 2 * D;

}

a[0] = 1 + dt * beta / 2 / sqr(dx) * D;

a[Nx - 1] = 1 + dt * alpha / 2 / sqr(dx) * D;

 

sweep(v);

 

 

for (int j = 0; j < Nx; j++) u[j] = v[j];

}

 

 

freopen("krank_nicholson_x", "w", stdout);

 

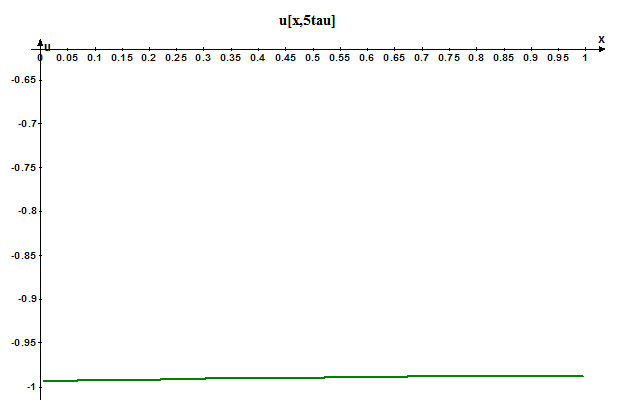
// зависимость от x:

 

for (int i = 0; i < Nx; i++) {

 

cout << (i + 0.5) * dx << " " << u[i] - (1 - exp(- 1.0 * tt / tau)) << "\n";

}

 

return 0;

 

}

 

При построении данных графиков для обеспечения устойчивости нам хватило Nx=40; Ny=6000.

 

 

 

 

Вывод:

Мы получили решение исходной задачи тремя методами. Графики решений соответствуют физическому смыслу задачи и достаточно хорошо соответствуют друг другу.

Метод суммирования ряда Фурье самый простой по сложности реализации и самый быстрый, но он требует полного аналитического решения задачи, и в этом смысле достаточно трудоемкий. Он вполне годится для построения графиков уже известных решений.

Явный метод Эйлера и метод Кранка-Николсона более сложны в написании и работают медленнее, особенно метод Кранка-Николсона, требующий большого количества вычислений на каждом шаге, но эти методы не требуют знания решения уравнения. Они также позволяют построить график решения с требуемой точностью. Пожалуй, самым эффективным является явный метод Эйлера, так как он требует гораздо меньше вычислений, чем метод Кранка-Николсона, хотя количество разбиений по времени в нем гораздо больше, и дает вполне приемлемую точность. Метод Кранка-Николсона гораздо более дорогой, но он обеспечивает нам безусловно устойчивое решение при достаточно малом количестве точек разбиения по времени.

 

Родственники

На данный момент самыми ближайшими родственниками русского языка являются восточнославянские языки: белорусский и украинский.

Южнославянские языки: болгарский, сербский, хорватский, македонский и словенский.

Западнославянские языки: польский, чешский, словацкий и лужицкий.