Тема 4. Риск и доходность финансовых активов
Инвестиционный портфель: понятие, виды, принципы формирования Наряду с недостатком средств, у предприятия может появляться избыток наличности, превышающий запланированный уровень, необходимый для осуществления текущей деятельности, реализации сделок или поддержания компенсационных остатков, который может быть инвестирован в ценные бумаги. Решение об инвестировании свободной наличности в ценные бумаги включает в себя не только определение объёма инвестиций, но и типа ценной бумаги как объекта инвестиций, поскольку невозможно найти такой фондовый инструмент, который был бы одновременно высокодоходным, надежным и высоколиквидным. Привлекательность портфельного инвестирования как раз и заключается в распределении инвестиционного потенциала между различными группами активов. В зависимости от того, какие цели и задачи изначально стоят при формировании того или иного портфеля, выбирается определенное процентное соотношение между различными инструментами, составляющими портфель инвестора. Портфельные инвестиции обладают следующими преимуществами [6, с.46]: - с помощью такого инвестирования можно придать совокупности ценных бумаг, объединенных в портфель, инвестиционные качества, которые не могут быть достигнуты при вложении средств в ценные бумаги какого-то одного эмитента; - высокая ликвидность и легкая управляемость – портфельное инвестирование гибко, вложения могут быть использованы в качестве залога, из него можно выйти с незначительными потерями, состав и структуру финансовых инструментов можно подстраивать под задачи оперативного и тактического менеджмента предприятия; - портфель ценных бумаг требует относительно невысоких затрат в сравнении с инвестированием в реальные активы, поэтому является доступным для значительного числа индивидуальных инвесторов; - портфель ценных бумаг на практике обеспечивает получение достаточно высоких доходов за относительно короткий временной интервал; - быстрее и легче реализовать благодаря наличию организованного фондового рынка с развитой информационной и торговой инфраструктурой. В портфель ценных бумаг могут входить ценные бумаги одного типа (акции) или различные инвестиционные ценности (акции, облигации, сберегательные и депозитные сертификаты, залоговые свидетельства, страховой полис и др.) Таким образом, под портфелем ценных бумаг понимается совокупность ценных бумаг, принадлежащих физическому или юридическому лицу, на праве собственности, с различными сроками погашения, неодинаковой ликвидностью и уровнем финансового риска, выступающая как целостный объект управления.
Классификация портфелей ценных бумаг по целям формирования. Выделяют два основных типа портфеля: портфель, направленный на преимущественный прирост курсовой стоимости входящих в него инвестиционных ценностей (портфель роста) и портфель, ориентированный на преимущественное получение высокого дохода за счет процентов и дивидендов (портфель дохода). Портфели роста имеют разновидности - портфель высокого роста (агрессивный) нацелен на максимальный прирост капитала. В его состав входят ценные бумаги молодых, быстрорастущих компаний, такие инвестиции более рискованны, но могут приносить и самый высокий доход; - портфель умеренного роста (консервативный) является наименее рискованным. Состоит в основном из ценных бумаг (обычно облигаций) хорошо известных компаний, характеризующихся невысокими, но устойчивыми темпами роста курсовой стоимости. Состав портфеля остается стабильным в течение длительного периода времени и нацелен на сохранение капитала; - портфель среднего роста (средний) - сочетание инвестиционных свойств портфелей умеренного и высокого роста. При этом гарантируется средний прирост капитала и умеренная степень риска. В портфель дохода должны включаться акции, предполагающие умеренный рост курсовой стоимости и высокие дивиденды, облигации и другие ценные бумаги, обеспечивающие высокие текущие выплаты. Портфель постоянного дохода - это портфель, который состоит из высоконадежных ценных бумаг и приносит средний доход при минимальном уровне риска; портфель высокого дохода включает высокодоходные ценные бумаги, приносящие высокий доход при среднем уровне риска. Комбинированный портфель формируется для снижения возможных потерь на фондовом рынке, как от падения курсовой стоимости, так и низких дивидендных и процентных выплат. Одна часть финансовых активов приносит владельцу увеличение его капитала в связи с ростом курсовой стоимости, а другая доход благодаря получению дивидендов и процентов, такой портфель включает обыкновенные и привилегированные акции, корпоративные и государственные облигации. Сбалансированный портфель предполагает сбалансированность не только доходов, но и риска, и поэтому в определенной пропорции состоит из ценных бумаг с быстрорастущей курсовой стоимостью и из высокодоходных ценных бумаг. В состав портфеля могут включаться и высокорисковые ценные бумаги. Обычно в состав данного портфеля включаются обыкновенные и привилегированные акции, а также облигации. На рисунке 1 приведена схема инвестиционных свойств ценных бумаг, включаемых при формировании инвестиционного портфеля.
Рисунок 1 - Классификация инвестиционного портфеля по инвестиционным свойствам
Помимо классификации инвестиционных портфелей в зависимости от степени риска, выделяют также и тип инвестора. При формировании инвестиционной политики определенное значение имеют индивидуальные склонности человека к риску: одни предпочитают действовать осторожно, не претендуя на большой доход, другие же могут идти на очень большой риск ради получения высокого дохода. Поэтому, инвесторов подразделяют на консервативных, умеренно-агрессивных и агрессивных. Формирование инвестиционного портфеля в зависимости от типа инвестора отражено в таблице 1.
Таблица 1 - Инвестиционный портфель для различных инвесторов
Консервативный тип инвестора характеризуется склонностью к минимизации риска, и надежности вложений. Умеренно-агрессивному типу инвестора присущи такие черты, как склонность к риску, но не очень высокому, предпочтение высокой доходности вложений, но с определенным уровнем защищенности. Агрессивный инвестор готов идти на больший риск ради получения высокой доходности.
Оценка доходности и риска инвестиционного портфеля. Практика показывает прямую пропорциональную зависимость доходности и риска, т.е. с ростом дохода растет и мера риска, его проявление связано со снижением доходности, либо прямыми финансовыми потерями. Теория портфельного инвестирования исходит из того, что значения доходности отдельной ценной бумаги портфеля являются случайными величинами, распределенными по нормальному (Гауссовскому) закону, т.е. доходности по альтернативным вложениям распределены нормально. Чтобы определить распределение вероятностей случайной величины доходности K необходимо знать, какие фактические значения Исследования западных экономистов показывают, что для рынка акций наиболее приемлемым является промежуток в 7-10 шагов расчета. Каждый результат имеет одинаковую вероятность, поскольку при n наблюдениях случайной величины вероятность конкретного результата составляет величину 1/n. Например, если исследуется доходность акции за предшествующие 10 лет, то вероятность каждой годовой доходности Ki составляет 1/10. Наиболее часто в теории инвестиционного портфеля используется среднее арифметическое значение случайных величин [7, с.195]:
где
n – количество лет, в течение которых велись наблюдения. Рассмотрим на примере, актива А, приведенного в таблице 2:
Таблица 2 – Характеристика активов при выборе портфеля
При покупке какого-либо актива инвестора интересует не только значение ожидаемой его доходности, но и уровень его риска. Рассчитанная по формуле (1) ожидаемая доходность является ее средней величиной в соответствии с динамикой доходности актива на фондовом рынке. Но на практике фактическая доходность будет отличаться от рассчитанной ожидаемой, всегда имеется некоторая степень риска не получить ожидаемой доходности. В практике управления портфелями ценных бумаг в качестве способа расчета величины риска используют показатели дисперсии и стандартного отклонения показателя фактической доходности от величины расчетной ожидаемой доходности, они учитывают отклонения доходности, как в сторону уменьшения, так и в сторону увеличения. Величина дисперсии актива
где
Чем выше этот показатель, тем больше разброс в доходностях, а значит и рискованнее актив, поэтому лучшим объектом инвестирования будет ценная бумага с наименьшей дисперсией. Используя данные предыдущего примера, для актива А:
Если мы рассчитаем дисперсии для актива B ( Также для характеристики риска финансового актива используется показатель среднеквадратического отклонения, который находится извлечением корня квадратного из дисперсии:
Для измерения последствий действий инвестора применяется коэффициент финансового риска:
где У – максимально возможная сумма убытка владельца актива; ФИ – сумма первоначальных затрат на инвестирование. Этот коэффициент выражает степень риска ведущего к банкротству:
Таким образом, в отношении риска финансовых активов, необходимо отметить 2 момента: 1) Т.к. доход – величина абсолютная и изменяется во времени, то целесообразней в качестве показателя использовать относительный показатель доходности. 2) С увеличением срока прогнозирования, точность его снижается, поэтому, чем более «длинным» является актив, тем он более рискован. Под ожидаемой доходностью портфеля понимается средневзвешенное значение ожидаемых значений доходности ценных бумаг, входящих в портфель. При этом «вес» каждой ценной бумаги определяется относительным количеством средств, направленных на ее покупку. Ожидаемая доходность инвестиционного портфеля равна [3, с.432]:
где
n – число ценных бумаг в портфеле. Оценивая риск конкретного актива из инвестиционного портфеля, можно действовать двояко: либо рассматривать этот актив изолированно от других активов, либо считать его неотъемлемой частью портфеля. При этом оценки риска актива и целесообразности операций с ним могут меняться. Например, актив, имеющий более высокий уровень риска при рассмотрении его изолированно, может оказаться практически безрисковым с позиции портфеля, при определенном сочетании входящих в этот портфель активов. Таким образом, риск актива - величина непостоянная, зависящая, в частности, от того, в каком контексте рассматривается данный актив: изолированно или как составная часть инвестиционного портфеля. При определении риска портфеля следует учитывать, что дисперсию портфеля нельзя найти как средневзвешенную величин дисперсий входящих в портфель ценных бумаг. Это объясняется тем, что дисперсия портфеля зависит не только от дисперсий ценных бумаг, но также и от взаимосвязи их доходностей друг с другом. Иными словами, риск портфеля объясняется не только индивидуальным риском каждой отдельно взятой ценной бумаги портфеля, но и тем, что существует риск воздействия изменений величин доходности одной акции на изменения доходности других акций, включаемых в инвестиционный портфель. Степень взаимозависимости двух случайных величин измеряют с помощью коэффициентов ковариации и корреляции. Ковариация представляет собой статистическую характеристику, отражающую степень сходства (различия) колебаний величин двух инструментов и рассчитывается по формуле:
где
n – общее количество лет наблюдения [7, с.197]
Принцип проявления этого показателя можно изобразить графически [2, с.79]. Ковариация доходности по двум финансовым активам варьируется в пределах от -1 до +1. Положительное значение ковариации говорит о том, что доходность активов изменяется в одном направлении, а отрицательное – в разных направлениях. Нулевое значение ковариации означает, что взаимосвязи между доходностями активов нет.
Рассчитаем ковариацию для активов А и В:
Мы видим, что доходности двух ценных бумаг не связаны, т.е. изменения доходностей этих активов происходят независимо друг от друга. Для характеристики степени связи между двумя переменными используется коэффициент корреляции
где
Значение этого коэффициента изменяется в тех же пределах, что и предыдущий показатель [8, с.198]. Как и в случае с отдельными активами, риск инвестиционного портфеля определяется вариацией его доходности. Пусть в исследуемый портфель входят n ценных бумаг; тогда дисперсия портфеля вычисляется по формуле:
или
где
Риск портфеля, измеряемый дисперсией, рассчитывается как взвешенная сумма ковариаций всех пар акций в портфеле, где каждая ковариация взвешена в системе весов каждой пары соответствующих акций, а дисперсия одной акции рассматривается как ковариация акции с самой собой, данные показатели отражены в таблице 3.
Таблица 3 – Риск портфеля при выборе финансовых активов
Для двух ценных бумаг, эта формула значительно упрощается:
Для портфеля из ценных бумаг А (50%) и В(50%), дисперсия составит:
В инвестиционном портфеле более рисковые активы уравновешиваются менее рисковыми. Благодаря портфельным инвестициям невозможно много выиграть, но также и нельзя крупно проиграть. Операции с конкретным активом оцениваются с точки зрения его влияния на общий риск портфеля, при наличии нескольких инструментов, которые потенциально могут быть включены в портфель, предпочтение не всегда отдается активу с меньшим риском. Увеличение числа включаемых активов, доходности которых разнонаправлены с доходностью портфеля, способствует снижению общего риска портфеля. Отсюда следует, что при включении в портфель активов, которые имеют низкие или отрицательные ковариации с другими активами портфеля, снижается сумма ковариаций, а, следовательно, и общий риск портфеля. При диверсификации риск портфеля снижается только до определенного уровня, ниже которого путем диверсификации риск уменьшить нельзя. Примерные количественные параметры, характеризующие зависимость общего риска портфеля (риска снижения совокупного дохода) от его структуры и пропорций между видами активов применительно к общему числу активов представлены в таблице 4. Таблица 4 – Изменение диверсифицируемого риска при различной структуре портфеля.
Наличие в портфеле уже 20-25 объектов инвестирования делает риск вложений относительно небольшим. Дальнейшее увеличение номенклатуры активов и увеличение степени диверсификации уже не играют существенной роли и могут даже привести к ухудшению доходности, повышению риска вследствие трудностей управления портфелем и сбора значительного объема нужной информации. Примитивная диверсификация игнорирует ковариацию (корреляцию) между доходностями ценных бумаг. Например, если в портфель включены 10 ценных бумаг одной отрасли, их доходы будут сильно коррелированны между собой, в то же время 5 акций в другом портфеле могут быть выпущены предприятиями различных отраслей, что обеспечить низкую корреляцию и низкую изменчивость дохода портфеля [4, с.150]. Таким образом, риск представляет собой сумму диверсифицируемого и недиверсифицируемого рисков. Диверсифицируемая часть риска представляет собой несистематический риск, а недиверсифицируемая – систематический. Классификация финансовых рисков представлена в таблице 5.
Таблица 5 - Классификация рисков на рынке ценных бумаг
Несистематический риск определяется факторами, связанными с деятельностью предприятия-эмитента и изменениями рыночной конъюнктуры. Систематический риск определяется глобальными обстоятельствами, не зависящими от инвестора и эмитента (политические события на уровне страны и на международном уровне, изменения законодательства и т.п.). Эти обстоятельства учитываются при формировании портфеля, основные подходы и этапы которого мы рассмотрим в следующей главе. Таким образом, доходность и риск инвестиционного портфеля – величины динамичные, поддающиеся в определенной мере регулированию, представляют собой комбинацию доходностей и рисков, входящих в него ценных бумаг.
Оценка сформированного инвестиционного портфеля. Измерение и оценка эффективности управления портфелем - конечная фаза цикла управления портфелем активов. Результаты оценки призваны обозначить правильность выбранной менеджером портфеля стратегии и тактики управления, ее реализации, а также служат информацией для корректировки ошибок и формирования более эффективных методов управления. Основными показателями, характеризующими результаты сформированного портфеля является доходность за период, внутренняя доходность и доходность на основе средней геометрической [9, с.879]. Доходность за период рассчитывается, если денежные средства инвестируются на определенный период:
где P – стоимость портфеля в начале периода n;
Период может быть любым – месяц, квартал, год и т.д. Для сравнения доходностей нескольких портфелей, их доходности приводится к единому временному периоду, в основном это год. Как правило, в ходе управления портфелем средства изымаются и вносятся дополнительно. Если это происходит в начале инвестиционного периода или перед окончанием, влияние этих сумм на итоговый результат будет незначительным. В случае же, когда приток и отток средств происходит постоянно, используются другие методы. Внутренняя доходность рассчитывается для определенного потока платежей. Она рассчитывается как ставка дисконтирования, приравнивающая потоки платежей, производимые в период управления и стоимость в конце периода к стоимости в начале периода. Например, в начале периода инвестируется 6,25 тыс. руб., через 3 месяца вносится дополнительно 2 тыс. руб., еще через 3 месяца изымается 3 тыс. руб., стоимость портфеля через 9 месяцев равна 6 тыс. руб. доходность будет равна 15,43%:
Внесение дополнительных средств отражается с минусом, т.к. это не результат деятельности менеджера, а приток денег, отток берется со знаком плюс. Для определения доходности на основе средней геометрической, необходимо знать стоимость портфеля на момент изъятия или получения дополнительных средств. Например, если перед поступлением 2 тыс. руб. стоимость портфеля выросла до 7 тыс. руб., его доходность составит:
В начале второго квартала после добавления в портфель 2 тыс. руб. его стоимость возросла до 9 тыс. руб. Предположим, что в конце второго квартала стоимость портфеля составила 9,5 тыс. руб. Тогда его доходность за отмеченный период равна:
В конце второго квартала из портфеля было изъято 3 тыс. руб., и стоимость его составила 6 тыс. руб. Поскольку в конце третьего периода портфель также стоил 6 тыс. руб., его доходность за третий квартал равна:
Средняя доходность за квартал составила:
В пересчете на год с учетом простого процента доходность равна 5,7 × 4 = 22,8%, а эффективная доходность составляет: (1 + 0,057)×4 - 1 = 0,2482 или 24,82% Оценка доходности по двум методам показала существенные отличия. Для определения доходности портфеля более точным является метод геометрической средней. Недостаток метода внутренней доходности в том, что на итоговое значение доходности портфеля влияет изъятие и инвестирование средств. Поэтому доходность портфеля следует учитывать по методу средней геометрической. Запишем его в общей форме:
где Формула предполагает, что периоды t равны друг другу, при решении уравнения получаем доходность портфеля за период t. Неудобство метода средней геометрической в том, что необходимо знать стоимость портфеля на каждый момент внесения или изъятия денег. Средства могут вноситься или изыматься с различной периодичностью. Поэтому не всегда период Если в рамках года изъятия и поступления средств происходят с разной периодичностью, необходимо определить стоимость портфеля на каждый момент движения средств, и рассчитать темп роста доходности портфеля, т.е. величину
где
После этого доходность в расчете на год находим по формуле:
где m – число периодов, из которых складывается год. В начале года стоимость портфеля составляла 10 тыс. руб. Через 200 дней она выросла до 14 тыс. руб. и в портфель было добавлено еще 6 тыс. руб. По завершении года стоимость портфеля составила 25 тыс. руб. Необходимо определить доходность портфеля за истекший период. Темп роста доходности за первые 200 дней равен 14:10 = 1,4, темп роста доходности за оставшиеся 165 дней равен 25:20 = 1,25, доходность портфеля за год составляет 1,4x1,25 - 1 = 0,75 или 75%. Как следует из представленного примера, для определения доходности можно не вычислять отдельно темп роста доходности для каждого периода, а записать одно уравнение, используя стоимости портфеля в начале и конце каждого временного отрезка. Тогда формулу для определения доходности портфеля можно записать следующим образом:
где P1 - стоимость портфеля в начале года;
Р2 - стоимость портфеля в начале второго периода;
Рn - стоимость портфеля в начале последнего периода;
Согласно формуле доходность портфеля для приведенного примера равна:
Мы определили доходность портфеля в рамках одного года. Часто эффективность управления портфелем будет оцениваться за ряд лет. Поэтому если изъятия и добавления капитала осуществлялись с разной периодичностью во времени, то вначале следует определить доходность портфеля для каждого года по формуле (13) или (14) и после этого вычислить среднюю доходность в расчете на год за весь период по формуле (11). Например, доходность за первый год составила 20%, за второй - 40%, а за третий -10%. Доходность портфеля в расчете на год (средняя доходность) за трехлетний период равна:
В России наиболее распространенным методом измерения эффективности управления портфелем является расчет доходности, взвешенной по времени и доходность, взвешенная по деньгам. [90, с.881; 10, с.18]. Расчет доходности, взвешенной по времени, определяет доход на одну денежную единицу, вложенную в портфель в начале периода измерения:
где Vi -1 - рыночная стоимость портфеля на начало дня; V - рыночная стоимость портфеля на конец дня; Ii - вложения средств (инвестиции) в портфель за день; Wi - отзыв средств из портфеля за день. TWR за период (N дней):
Фактически это индекс портфеля, если у менеджера есть рубль, то он умножает его на коэффициент (TWR) и определяет доход на этот рубль в конце периода. Особенности данного метода: - зависимость от внесения и изъятия денег из портфеля в течение периода; - метод не учитывает динамичность движения денежных средств по позициям портфеля, поэтому его лучше использовать для анализа портфеля в целом, а не его отдельных позиций. - предполагает наличие рыночной стоимости актива, а для некоторых финансовых инструментов это не всегда возможно. Этих ограничений можно избежать при расчете доходности, взвешенной по деньгам, которая рассчитывается как отношение доход/убытки к среднеинвестируемому капиталу за период Ij:
Расчет Ij можно осуществлять на основе балансовой стоимости (БС), рыночной стоимости и платежей по транзакциям. Расчет числителя доходы/убытки (д/у) проводиться с помощью: рыночной оценки за период по разнице рыночной цены ценной бумаги в конце и начале рассматриваемого периода или учета доходов/убытков от транзакций и разницы рыночной и балансовой стоимости ценной бумаги на конец периода. При определении общих доходов/убытков независимо от выбранного способа расчета также можно учитывать: выплаты дивидендов/купонов; доходы/убытки от операций закрытия; затраты на управление портфелем; налоги; премии от опционов. Рекомендуется в числителе использовать следующий набор показателей: Общие д/у = реализованные д/у + нереализованные д/у + дивиденды/купоны. Другой вариант расчета доходов/убытков - использование только рыночной стоимости актива: Общие д/у рынка = Рыночная стоимость актива на конец периода - Рыночная стоимость актива на начало периода + Платежи за период. Если сравнивать практичность использования TWR и MWR, то необходимо отметить, что: TWR рекомендуется как стандартный, хорошо известный метод оценки портфеля. Технология расчета этой доходности похожа на расчет индекса, поэтому TWR наиболее подходит для сравнения с другими рыночными индексами. В связи с этим он наиболее пригоден для отчетов клиентам. MWR имеет больше «степеней свободы» в расчетах и дает портфельному менеджеру больше возможностей при анализе отдельных позиций и портфеля в целом. Поэтому данный метод рекомендуется для аналитической работы портфельного менеджера. Подводя итог, можно сказать, что выбор того или иного метода напрямую зависит от цели, которую преследует инвестор.
|


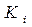 принимает данная величина, и какова вероятность
принимает данная величина, и какова вероятность  каждого подобного результата. При этом инвестора интересует доходность инвестиций в конце инвестиционного периода, то есть будущие значения
каждого подобного результата. При этом инвестора интересует доходность инвестиций в конце инвестиционного периода, то есть будущие значения  , которые в начальный момент инвестирования неизвестны, поэтому инвестор оперирует ожидаемым, будущим распределением случайной величины K. В основе его расчета лежит предположение о том, что распределение вероятностей ожидаемых величин практически совпадает с распределением вероятностей уже наблюдавшихся фактических величин, значит, чтобы получить распределение случайной величины K в будущем достаточно построить распределение этих величин за какой-то промежуток времени в прошлом.
, которые в начальный момент инвестирования неизвестны, поэтому инвестор оперирует ожидаемым, будущим распределением случайной величины K. В основе его расчета лежит предположение о том, что распределение вероятностей ожидаемых величин практически совпадает с распределением вероятностей уже наблюдавшихся фактических величин, значит, чтобы получить распределение случайной величины K в будущем достаточно построить распределение этих величин за какой-то промежуток времени в прошлом. , (1)
, (1) – среднее ожидаемое значение доходности;
– среднее ожидаемое значение доходности; – вероятности данных значений доходности;
– вероятности данных значений доходности;
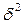 рассчитывается по формуле:
рассчитывается по формуле: (2),
(2), - ожидаемая доходность ценной бумаги в i-м периоде,
- ожидаемая доходность ценной бумаги в i-м периоде, - вероятность получения дохода в i-м периоде [7, с.196].
- вероятность получения дохода в i-м периоде [7, с.196].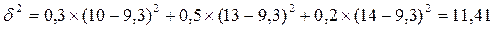
 =1,24) и C (
=1,24) и C ( (3)
(3) , (4)
, (4) 0,2 – оптимальный, не приводит к банкротству;
0,2 – оптимальный, не приводит к банкротству; , (4)
, (4) – ожидаемая норма отдачи портфеля;
– ожидаемая норма отдачи портфеля; – доля в общих инвестиционных расходах, идущая на приобретение i-ой ценной бумаги («вес» i-ой ценной бумаги в портфеле);
– доля в общих инвестиционных расходах, идущая на приобретение i-ой ценной бумаги («вес» i-ой ценной бумаги в портфеле);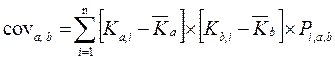 , (5)
, (5) – ковариация между величинами доходности ценной бумаги a и ценной бумаги b;
– ковариация между величинами доходности ценной бумаги a и ценной бумаги b;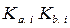 – доходность ценных бумаг a и b в момент времени i;
– доходность ценных бумаг a и b в момент времени i; ,
, 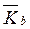 – ожидаемая (среднеарифметическая) доходность ценных бумаг a и b;
– ожидаемая (среднеарифметическая) доходность ценных бумаг a и b; - вероятности получения доходности по активам a и b.
- вероятности получения доходности по активам a и b.


 . Этот показатель не зависит от единиц измерения, характеризует силу и направление линейной связи между двумя переменными:
. Этот показатель не зависит от единиц измерения, характеризует силу и направление линейной связи между двумя переменными: , (6)
, (6) – ковариация доходности активов А и В;
– ковариация доходности активов А и В; ,
,  – стандартные отклонения доходности активов А и В.
– стандартные отклонения доходности активов А и В.
 (7)
(7)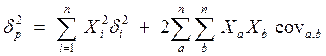 , (8)
, (8) - стандартное отклонение доходности i-го актива
- стандартное отклонение доходности i-го актива – корреляция доходностей активов А и В;
– корреляция доходностей активов А и В; (9)
(9)
 , 10)
, 10) – стоимость портфеля в конце периода n.
– стоимость портфеля в конце периода n.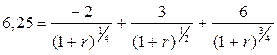
 или 12%
или 12%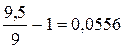 / 5,66%
/ 5,66%
 или 5,7%
или 5,7% (11)
(11) - средняя доходность портфеля за период t;
- средняя доходность портфеля за период t;  - доходность за i-й период, n – число периодов, П – знак произведения.
- доходность за i-й период, n – число периодов, П – знак произведения. будет равен периоду
будет равен периоду  и т.д. Если инвестор осуществляет дополнительные взносы или изъятия средств незадолго до окончания или начала каждого периода, можно сделать допущение о том, что данные действия приходятся на конец (начало) периода и воспользоваться формулой без изменений. Небольшая временная погрешность, как правило, не скажется на доходности портфеля значительно. Если поступления или изъятия средств происходят с равной периодичностью, но в одном из периодов в его середине также наблюдается изъятие или поступление денег от клиента, вначале можно определить доходность за данный период и после воспользоваться формулой.
и т.д. Если инвестор осуществляет дополнительные взносы или изъятия средств незадолго до окончания или начала каждого периода, можно сделать допущение о том, что данные действия приходятся на конец (начало) периода и воспользоваться формулой без изменений. Небольшая временная погрешность, как правило, не скажется на доходности портфеля значительно. Если поступления или изъятия средств происходят с равной периодичностью, но в одном из периодов в его середине также наблюдается изъятие или поступление денег от клиента, вначале можно определить доходность за данный период и после воспользоваться формулой. для каждого отрезка времени по формуле:
для каждого отрезка времени по формуле: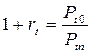 , (12)
, (12) - стоимость портфеля в конце периода t;
- стоимость портфеля в конце периода t;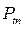 - стоимость портфеля в начале периода t.
- стоимость портфеля в начале периода t. , (13)
, (13)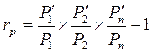 , (14)
, (14) - стоимость портфеля в конце первого периода;
- стоимость портфеля в конце первого периода; - стоимость портфеля в конце второго периода;
- стоимость портфеля в конце второго периода; - стоимость портфеля в конце года.
- стоимость портфеля в конце года.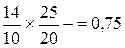 или 75%.
или 75%.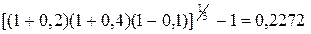 или 22,72%
или 22,72% , (15)
, (15) (16)
(16) (17)
(17)


