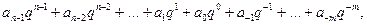СИСТЕМЫ СЧИСЛЕНИЯ.

В многовидовом море информации в качестве универсального вида ее представления на компьютере выступают данные в виде различных цифровых кодов. Для записи информации о количестве объектов используются числа. Числа записываются с использованием особых знаковых систем, которые называются системами счисления. Алфавит систем счисления состоит из символов, которые называются цифрами. В связи с этим необходимо ввести понятие системы счисления. Под системой счисления понимают совокупность способов представления и записи чисел. Система счисления – это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита, называемых цифрами. Она представляет математическую модель, позволяющую преобразовать информацию с помощью кода. В зависимости от способа изображения чисел системы делятся на позиционные и непозиционные:

Ø позиционные, когда значение каждой цифры числа определяется ее местом (позицией) в записи числа;

Ø непозиционные, когда значение цифры в числе не зависит от ее места в записи числа.

Количество цифр, используемых для изображения числа в позиционной системе счисления, называется основанием системы.

 

СИСТЕМА СЧИСЛЕНИЯ	ОСНОВАНИЕ	АЛФАВИТ ЦИФР
ПОЗИЦИОННЫЕ
Десятичная		0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Двоичная		0, 1
Восьмеричная		0, 1, 2, 3, 4, 5, 6, 7, 8
Шестнадцатеричная		0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
НЕПОЗИЦИОННАЯ
Римская		I(1), V(5), X(10), L(50), C(100), D(500), M(1000)

 

Непозиционная система счисления - система счисления, у которой количественное значение цифры зависит только от ее написания, значение цифры не зависит от ее положения в числе. К такой системе счисления относятся, например, римские цифры. В числе ХХХ (30) цифра Х встречается трижды и, в каждом случае, обозначает одну и ту же величину – число 10, три раза по 10 в сумме дают 30. Величина числа в непозиционных системах счисления определяется как сумма или разность цифр в числе. Если меньшая цифра стоит слева от большей, то она вычитается, если справа – прибавляется. Например, запись десятичного числа 1998 в римской системе счисления будет выглядеть следующим образом:

MCMXCVIII = 1000 + (1000 – 100) + (100 – 10) + 5 + 1 + 1 + 1

Система счисления называется позиционной, если значение каждой цифры, входящей в число, определяется ее местом в ряду цифр, составляющих это число. Позиционные системы характеризуются определенным алфавитом и основанием. Количество различных цифр, применяемых в позиционной системе счисления, называется основанием системы. Наиболее распространенными позиционными системами счисления являются десятичная, двоичная, восьмеричная и шестнадцатеричная. Десятичная система счисления имеет алфавит цифр, который состоит из десяти, так называемых арабских, цифр и основание равное – 10, двоичная – две цифры и основание 2, восьмеричная – восемь и основание 8, шестнадцатеричная – шестнадцать цифр (в качестве цифр используются и буквы латинского алфавита) и основание 16. В позиционных системах счисления количественное значение цифры зависит от ее позиции в числе, основание системы равно количеству цифр (знаков в ее алфавите) и определяет, во сколько раз различаются значения цифр соседних разрядов числа.

Первая позиционная система счисления была придумана еще в древнем Вавилоне, причем вавилонская нумерация была не десятичной, а шестидесятеричной, т.е. в ней использовалось шестьдесят цифр. Интересно, что до сих пор при измерении времени используется основание равное 60 (в 1 минуте содержится 60 секунд, а в часе – 60 минут).

Разряд числа возрастает от младших разрядов к старшим справа налево. Например, в десятичной системе крайняя справа позиция соответствует минимальному значению, в которой цифра обозначает единицы, цифра, смещенная на одну позицию влево, обозначает десятки, еще левее – сотни, а затем тысячи и т.д. В качестве примера рассмотрим число 555. Цифра 5 встречается трижды, причем самая правая обозначает пять единиц, вторая справа – пять десятков, наконец, третья – пять сотен. Такая запись числа является записью в сокращенной форме. В полной форме запись числа 555 в десятичной системе должна выглядеть следующим образом:

555₁₀ = 5*10² + 5*10¹ + 5*10⁰

Число в позиционных системах счисления записывается в виде суммы ряда степеней основания (в данном случае 10) с коэффициентами, в качестве которых выступают цифры данной системы счисления.

Сравним двоичную и десятичную системы счисления. Обе системы позиционные, т.е. «вес» цифры в числе зависит от ее позиции, однако они различаются набором используемых цифр и основанием.

Цифры являются различными состояниями, которые должен уметь записывать, хранить и распознавать пользователь системы счисления. Людям в силу ряда причин (в частности, наличия десяти пальцев на руках) удобно использовать десять цифр. Компьютер использует две цифры, так как до сих пор не удается создать надежно работающие технические устройства, которые могли бы со стопроцентной надежностью сохранять и распознавать большее, чем два, количество различных состояний (цифр). Для двух состояний такое устройство существует – это триггер.

Основание в системе счисления определяет перенос в старший разряд числа. Чем меньше основание, тем быстрее растет разрядность числа. Человеку очень трудно воспринимать многоразрядные числа, и поэтому он с трудом воспринимает двоичные числа. Для компьютера, наоборот, разрядность числа не имеет большого значения, так как современные компьютеры обрабатывают за один такт работы процессора до 64 двоичных разрядов.

В двоичной системе основание равно 2, а алфавит цифр включает два числа 0 и 1. Следовательно, числа в двоичной системе в полной форме записываются в виде суммы степеней основания 2 с коэффициентами, в качестве которых выступают цифры 0 или 1. Например, число 5 в двоичной системе в полной форме записывается следующим образом:

5 = 1*2² + 0*2¹ + 1*2⁰

В сокращенной и более привычной форме число 5 в двоичной системе записывается так: 5 = 101₂.

Запись чисел в каждой из систем счисления с основанием q означает сокращенную запись выражения

где a_i – цифры системы счисления; n и m – число целых и дробных разрядов соответственно.

При переводе целого десятичного числа в систему с основанием q его необходимо последовательно делить на q до тех пор, пока не останется остаток, меньший или равный q-1. Число в системе с основанием q представлено как последовательность остатков от деления, записанных в обратном порядке, начиная с последнего.