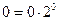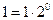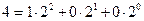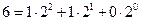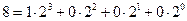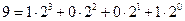ШЕСТНАДЦАТЕРИЧНУЮ
Перевод чисел из десятичной системы в двоичную, восьмеричную и шестнадцатеричную более сложен и может осуществляться различными способами. Рассмотрим один из алгоритмов перевода на примере чисел из десятичной системы в двоичную, при этом необходимо учитывать, что алгоритмы перевода целых и правильных дробей будут различаться. Алгоритм перевода целых десятичных чисел в двоичную систему счисления. Пусть Ацд – целое десятичное число, разложим его в ряд по основанию 2. Тогда в его записи в развернутой форме отсутствуют отрицательные степени основания, т.е. числа 2:
На первом шаге разделим число Ацд на основание двоичной системы, т.е. на 2. Частное от деления будет равно:
а остаток равен На втором шаге целое частное опять разделим на 2, остаток от деления будет Если продолжать этот процесс деления, то после n -го шага получим последовательность остатков:
Легко заметить, что их последовательность совпадает с обратной последовательностью цифр целого двоичного числа, записанного в свернутой форме: Таким образом, достаточно записать остатки в обратной последовательности, чтобы получить искомое двоичное число. Алгоритм перевода целого десятичного числа в двоичное будет следующим:
В качестве примера рассмотрим перевод десятичного числа 19 в двоичную систему, записывая результаты в таблицу:
В результате получаем двоичное число: Алгоритм перевода десятичных дробей в двоичную систему счисления. Пусть Адд – десятичная дробь, разложим ее в ряд по основанию 2. Тогда в его записи в развернутой форме отсутствуют положительные степени основания, т.е. числа 2:
На первом шаге умножим число Адд на основание двоичной системы, т.е. на 2. Произведение будет равно:
Целая часть равна a -1, именно это число и является значением первого дробного разряда двоичного числа. На втором шаге оставшуюся дробную часть опять умножим на 2, получим целую часть, равную Описанный процесс необходимо продолжать до тех пор, пока в результате умножения не получим нулевую дробную часть или не будет достигнута требуемая точность вычислений. Легко заметить, что последовательность полученных чисел совпадает с последовательностью цифр дробного двоичного числа, записанного в свернутой форме: Алгоритм перевода десятичной дроби в двоичную будет следующим:
В качестве примера, рассмотрим перевод десятичной дроби 0,75 в двоичную, записывая результаты в таблицу:
В результате получаем двоичную дробь:
ТАБЛИЦА ПЕРЕВОДА ДЕСЯТИЧНЫХ ЧИСЕЛ В ДВОИЧНЫЕ ЧИСЛА
|

 .
.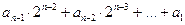 ,
,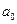 .
.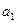 .
. .
. .
. .
.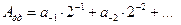
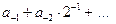
 , именно это число и является значением второго дробного разряда двоичного числа.
, именно это число и является значением второго дробного разряда двоичного числа. .
.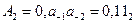 .
.