Допустим, что физическая величина 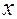 находится в некоторой функциональной зависимости от других
находится в некоторой функциональной зависимости от других  , при этом
, при этом  можно непосредственно измерить приборами.
можно непосредственно измерить приборами.
Пусть также мы провели несколько измерений каждой из величин  и получили ряд значений
и получили ряд значений  (число измерений каждого из аргументов не обязательно одинаково).
(число измерений каждого из аргументов не обязательно одинаково).
Как и прежде для искомой 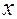 необходимо определить
необходимо определить 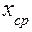 и указать с заданной доверительной вероятностью интервал, в котором лежит её истинное значение. Для этого необходимо обработать по методике прямых измерений каждую из величин
и указать с заданной доверительной вероятностью интервал, в котором лежит её истинное значение. Для этого необходимо обработать по методике прямых измерений каждую из величин  (по формулам 1-7 вычислить
(по формулам 1-7 вычислить  – средние значения;
– средние значения;  – полные ошибки и
– полные ошибки и  – относительные погрешности). Затем вычисляют среднее значение
– относительные погрешности). Затем вычисляют среднее значение 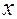
 . (9)
. (9)
Определить погрешность в случае произвольной функциональной зависимости  , можно применив следующую формулу
, можно применив следующую формулу
 (10)
(10)
где  ,
, 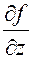 ,
,  – частные производные
– частные производные  , вычисленные по средним значениям
, вычисленные по средним значениям  , а
, а  – соответствующие полные ошибки.
– соответствующие полные ошибки.
Как показывает практика проведения лабораторных занятий, эта формула вызывает затруднения у студентов. В этой связи рассмотрим наиболее часто встречающиеся случаи функциональной зависимости  .
.
А) Пусть  .
.
Тогда 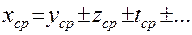 , а полная ошибка
, а полная ошибка
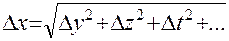 . (11)
. (11)
Б) Пусть  .
.
В этом случае сначала найдем относительную погрешность  :
:
 , (12)
, (12)
Учитывая что, 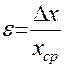 , получим
, получим
 . (13)
. (13)
Заметим, что в выражениях 10,11 суммируются квадраты величин. Возможно, некоторыми из них можно пренебречь (см. пример 2).
После вычислений остается записать ответ: 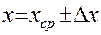 ,
,  (%).
(%).
Обработка результатов по методике косвенных измерений довольно трудоемкий процесс, вычисления можно существенно упростить, применив к косвенным измерениям методику прямых измерений. А именно из полученного ряда значений  необходимо сосчитать несколько различных значений
необходимо сосчитать несколько различных значений 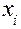 [
[  ,
,  , …,
, …,  , можно комбинировать индексы у аргументов] и полагая, что они получены в результате непосредственного измерения, применить формулы 1-4. В этом случае, ни о какой инструментальной погрешности речи уже не идет и полная ошибка
, можно комбинировать индексы у аргументов] и полагая, что они получены в результате непосредственного измерения, применить формулы 1-4. В этом случае, ни о какой инструментальной погрешности речи уже не идет и полная ошибка  . Однако, пользоваться таким упрощением необходимо с осмотрительностью. (Запрещается в случае, когда нельзя пренебречь инструментальной погрешностью). Тем не менее, в большинстве лабораторных работ по физике это возможно. Окончательно записываем ответ в виде:
. Однако, пользоваться таким упрощением необходимо с осмотрительностью. (Запрещается в случае, когда нельзя пренебречь инструментальной погрешностью). Тем не менее, в большинстве лабораторных работ по физике это возможно. Окончательно записываем ответ в виде: 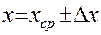 ,
,  (%).
(%).

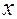 находится в некоторой функциональной зависимости от других
находится в некоторой функциональной зависимости от других  , при этом
, при этом  можно непосредственно измерить приборами.
можно непосредственно измерить приборами. и получили ряд значений
и получили ряд значений  (число измерений каждого из аргументов не обязательно одинаково).
(число измерений каждого из аргументов не обязательно одинаково).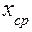 и указать с заданной доверительной вероятностью интервал, в котором лежит её истинное значение. Для этого необходимо обработать по методике прямых измерений каждую из величин
и указать с заданной доверительной вероятностью интервал, в котором лежит её истинное значение. Для этого необходимо обработать по методике прямых измерений каждую из величин  – средние значения;
– средние значения;  – полные ошибки и
– полные ошибки и  – относительные погрешности). Затем вычисляют среднее значение
– относительные погрешности). Затем вычисляют среднее значение  . (9)
. (9) (10)
(10) ,
, 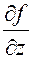 ,
,  – частные производные
– частные производные  , вычисленные по средним значениям
, вычисленные по средним значениям  .
.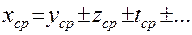 , а полная ошибка
, а полная ошибка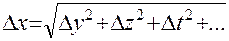 . (11)
. (11) .
. :
: , (12)
, (12)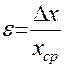 , получим
, получим . (13)
. (13)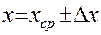 ,
,  (%).
(%). необходимо сосчитать несколько различных значений
необходимо сосчитать несколько различных значений 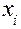 [
[  ,
,  , …,
, …,  , можно комбинировать индексы у аргументов] и полагая, что они получены в результате непосредственного измерения, применить формулы 1-4. В этом случае, ни о какой инструментальной погрешности речи уже не идет и полная ошибка
, можно комбинировать индексы у аргументов] и полагая, что они получены в результате непосредственного измерения, применить формулы 1-4. В этом случае, ни о какой инструментальной погрешности речи уже не идет и полная ошибка  . Однако, пользоваться таким упрощением необходимо с осмотрительностью. (Запрещается в случае, когда нельзя пренебречь инструментальной погрешностью). Тем не менее, в большинстве лабораторных работ по физике это возможно. Окончательно записываем ответ в виде:
. Однако, пользоваться таким упрощением необходимо с осмотрительностью. (Запрещается в случае, когда нельзя пренебречь инструментальной погрешностью). Тем не менее, в большинстве лабораторных работ по физике это возможно. Окончательно записываем ответ в виде: 


