САМАРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ
Эта задача имеет самое непосредственное отношение к задачам оптимизации. Рассмотрим метод Ньютона. Пусть имеется система нелинейных уравнений
Итерационная процедура представляется в виде
Введем обозначения
Предполагая малость приращений
где
Предположим, что
для сходимости метода вводится параметр
Отметим некоторые недостатки метода. 1. Метод требует хорошего начального приближения. При плохом начальном приближении процесс может вообще расходиться. 2. На каждом шаге нужно решать систему линейных уравнений, что может потребовать больших временных затрат. 3. Есть проблемы с вычислением матрицы Якоби. Каждый элемент матрицы надо определять разностным методом. Есть так называемые квазиньютоновские методы, которые, в основном, направлены на упрощение расчета матрицы Якоби.
САМАРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ
Кафедра “Управление эксплуатационной работой, станции и узлы”
|
(1)
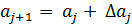
– значение вектор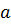а 
на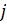 
–й итерации.
.
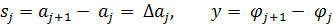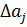разложим в ряд Тейлора вектор-функции 
, оставляя только члены не выше первого порядка малости.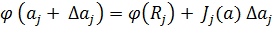
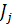– матрица Якоби в точке 
.
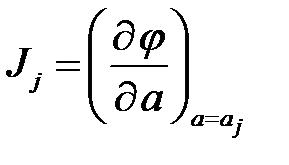и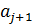 
есть решение (1), т.е. 
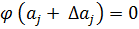, тогда для определения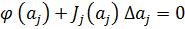 
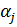, регулирующий величину шага 
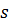, т.е.
