Основные теоретические сведения. 1. Брускин Д.Э. и др. Электрические машины: В 2-х ч.Ч.1 /
Л. К. Андрусевич А.А.Ищук Антенно - фидерные устройства Методические указания К лабораторным работам Новосибирск
Лабораторная работа № 1
Исследование симметричного вибратора Цель работы: Исследование направленных свойств и электрических характеристик симметричных вибраторов.
Основные теоретические сведения Симметричным вибратором называется проволочная антенна, имеющая два одинаковых плеча, питаемых в противофазе (рис. 1.1).
Рис.1.1. Симметричный вибратор
При анализе работы симметричного вибратора решаются две задачи – внутренняя задача и внешняя. Внутренняя задача имеет целью определение законов распределения тока и напряжения по вибратору для получения требуемых электрических характеристик вибратора. Целью внешней задачи является определение поля излучения в произвольной точке пространства по известным законам распределения тока и напряжения по вибратору. Внутренняя задача предполагает строгое решение системы волновых уравнений с граничными условиями. В практических задачах широкое применение имеет инженерный метод определения законов распределения тока и напряжения по вибратору, в котором в качестве прототипа вибратора используется двухпроводная длинная линия, разомкнутая на конце. Двухпроводная линия не излучает электромагнитные волны, если расстояние между проводами d много меньше длины волны (рис. 1.2). Это объясняется тем, что токи, текущие в проводах в противоположных направлениях, излучают поля в противофазе, поэтому результирующее поле излучения равняется нулю. Если провода двухпроводной линии развернуть в одну линию, то токи в проводах будут течь в одном направлении, и такая деформированная линия становится излучателем (т.е., симметричным вибратором, рис. 1.). С определенной погрешностью при этом можно считать, что законы распределения тока и напряжения существенно не изменятся.
Рис.1.2. Формирование симметричного вибратора на основе длинной линии Используя двухпроводную линию в качестве прототипа, можно без труда определить, как изменяется величина тока и напряжения вдоль вибраторов различной длины. Для вибратора, диаметр которого много меньше его длины, в первом приближении можно полагать, что амплитуда тока вдоль его длины изменяется по синусоидальному закону в случае гармонического сигнала. В вибраторе, как и в длинной линии, разомкнутой на конце, устанавливается режим стоячей волны, причем узел тока (пучность напряжения) находится всегда на концах вибратора. На рис. 1.3, 1.4 приведены эпюры распределения тока и напряжения вдоль вибратора с длиной плеча
а) ℓ = 0,25λ, б) ℓ = 0,5λ
Рис.1.4. Эпюры тока и напряжения и диаграммы направленности симметричного вибратора с длиной плеча: а) ℓ = 0,75λ, б) ℓ = λ
Внешняя задача также имеет строгое решение на основании системы волновых уравнений с учетом граничных условий. Однако задача существенно упрощается, если использовать метод геометрической оптики. В соответствии с этим методом симметричный вибратор конечной длины можно представить совокупностью элементарных электрических излучателей, образующих линейную антенную решетку. Результирующее поле в произвольной точке пространства представляет собой геометрическую сумму полей отдельных элементов решетки. Под этим понимается сложение полей отдельных источников с учетом их амплитуд и фаз:
Учитывая, что количество элементов в решетке бесконечное множество, операцию сложения заменяют интегрированием по длине вибратора:
где: к – волновое число, Iп – амплитуда тока в пучности, ℓ - длина плеча вибратора, j - текущий угол, который отсчитывается от нормали к оси вибратора. Первый множитель является фазовым множителем результирующего поля, второй определяет его амплитуду, третий – зависимость амплитуды поля от угла обхода вибратора по окружности произвольного радиуса r. Последний множитель называется диаграммой направленности симметричного вибратора:
Диаграммы направленности в полярных или в декартовых координатах обычно строят в нормированном виде Как следует из формулы (1.2), форма диаграммы направленности зависит от электрической длины вибратора По мере роста отношения Многолепестковый характер диаграммы направленности объ-ясняется интерференцией полей элементарных излучателей, входящих в состав симметричного вибратора. Если длина вибратора 2ℓ не превышает λ, то вся совокупность элементарных излучателей представляет собой синфазную неравноамплитудную решетку. Пусть точка наблюдения находится на окружности радиуса r (рис.1.6). При условии, что кr >> 1, радиусы – векторы от элементарных источников до точки наблюдения без большой погрешности можно принять как систему параллельных линий. При j = 0 расстояние от отдельных элементарных излучателей до точки наблюден практически одинаковы, поэтому будут одинаковы и фазы полей, создаваемых этими излучателями в точке наблюдения.
Если точка наблюдения сместится по окружности на некоторый угол j, то из-за возникшей при этом разности хода Dr поля в точке наблюдения будут сдвинуты по фазе на определенный угол. Причем наибольший сдвиг фаз будут иметь поля, создаваемые крайними элементами вибратора. Если длина вибратора превышает λ, то в плечах вибратора появляются участки с противоположным направлением тока. В результате этого фаза поля, создаваемого каждым элементарным излучателем в пункте наблюдения, будет определяться не только расстоянием до точки наблюдения, но также фазой питающего тока. При разности хода полей от крайних элементов Dr, кратной 0,5l (Dj = mp, m = 1, 2, 3…), в диаграмме направленности вибратора будут минимумы, а при Dr, кратной l (Dj = m . 2p) - максимумы. Остальные участки плеч вибратора влияют в основном на уровень боковых лепестков. Теперь становится понятным, почему диаграммы направленности вибратора с длиной Подобные рассуждения остаются справедливыми при анализе диаграммы направленности любых антенн (включая антенные решетки и антенны поверхностного типа). Для согласования симметричного вибратора с питающей линией (фидером) необходимо знать его входное сопротивление, т.е. отношение
где Iк, Uк – ток и напряжение в конце линии (на концах вибратора), wв – волновое сопротивление линии (вибратора) g = a + jк – постоянная распространения, a - коэффициент затухания, к = По определению для линии Где: Rп1 – погонное сопротивление потерь. Эта формула справедлива и для вибратора, однако в отличие от длинной линии потери энергии, подводимой к вибратору, определяются преимущественно не потерями на тепло (нагрев проводов), а излучением полезной мощности, т.е.
где: RS1 – погонное сопротивление излучения. Для вибраторов с длиной плеча ℓ = 0,25λ и ℓ = 0,5λ RS1 = откуда: где: RSп – сопротивление вибратора, отнесенное к пучности тока (рис.1.7). Поскольку Iк = 0 (как для разомкнутой линии):
Zвх = wвсthgℓ = wвcth [(a + jк)ℓ]. (1.7)
Окончательно формула (1.7) имеет вид:
Как следует из формулы (1.8), входное сопротивление вибратора имеет комплексный характер: Zвх = Rвх - jХвх (1.9)
Как и в длинной линии реактивная составляющая входного сопротивления вибратора в зависимости от его длины может иметь либо емкостный, либо индуктивный характер, а у вибраторов с длиной, кратной 0,25l она равна нулю. В этом случае вибратор называется резонансным или настроенным. Сопротивление излучения вибратора также является функцией его электрической длины как показано на графике рис.1.7.
|




 , ℓ = 0,75l, ℓ = λ.
, ℓ = 0,75l, ℓ = λ.


 .
. . Опуская промежуточные математические операции, приведем окончательную формулу для напряженности электрического поля, создаваемого симметричным вибратором:
. Опуская промежуточные математические операции, приведем окончательную формулу для напряженности электрического поля, создаваемого симметричным вибратором: (1.1)
(1.1) 
 (1.2)
(1.2) . На графике откладывают текущие значения F(j), поделенные на максимальное значение. В противном случае, диаграммы, построенные при различных уровнях поля, нельзя было бы сравнивать.
. На графике откладывают текущие значения F(j), поделенные на максимальное значение. В противном случае, диаграммы, построенные при различных уровнях поля, нельзя было бы сравнивать. . Наличие в формуле (1.2) периодических функций sin и cos является причиной того, что в общем случае диаграмма направленности имеет ряд максимумов и минимумов. Участки диаграммы между двумя соседними минимумами называются лепестками. При j=0 имеет место максимум главного лепестка. Остальные максимумы соответствуют вторичным или боковым лепесткам.
. Наличие в формуле (1.2) периодических функций sin и cos является причиной того, что в общем случае диаграмма направленности имеет ряд максимумов и минимумов. Участки диаграммы между двумя соседними минимумами называются лепестками. При j=0 имеет место максимум главного лепестка. Остальные максимумы соответствуют вторичным или боковым лепесткам. начинает появляться первый боковой лепесток. При
начинает появляться первый боковой лепесток. При  уровень бокового лепестка становится больше уровня главного лепестка, а при
уровень бокового лепестка становится больше уровня главного лепестка, а при  основной лепесток полностью исчезает (рис.1.3, 1.4). Ширина главного лепестка диаграммы направленности определяется либо по нулевому излучению (j0), либо по половинной мощности (j0,5) (рис. 1.5).
основной лепесток полностью исчезает (рис.1.3, 1.4). Ширина главного лепестка диаграммы направленности определяется либо по нулевому излучению (j0), либо по половинной мощности (j0,5) (рис. 1.5).

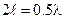 и 2ℓ = l не имеют боковых лепестков. Таким образом, именно электрическая длина вибратора определяет количество боковых лепестков.
и 2ℓ = l не имеют боковых лепестков. Таким образом, именно электрическая длина вибратора определяет количество боковых лепестков. . Подобно двухпроводной линии симметричный вибратор можно рассматривать как электрическую цепь с распределенными параметрами R, L, С. Используя математический аппарат, описывающий процессы в длинной линии, можно записать:
. Подобно двухпроводной линии симметричный вибратор можно рассматривать как электрическую цепь с распределенными параметрами R, L, С. Используя математический аппарат, описывающий процессы в длинной линии, можно записать: , (1.3)
, (1.3) .
.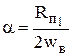 (1.4)
(1.4) , (1.5)
, (1.5) ,
,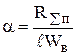 , (1.6)
, (1.6)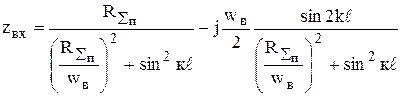 (1.8)
(1.8)



