Основные теоретические сведения. Параболическая антенна является одним из видов зеркальных антенн
Параболическая антенна является одним из видов зеркальных антенн. Основными элементами конструкции зеркальных антенн являются металлический рефлектор (зеркало) и слабонаправленная антенна, используемая в качестве облучателя рефлектора. В отличие от проволочных (вибраторных) антенн в зеркальных антеннах функции формирователя диаграммы направленности и функции источника возбуждения первичного поля разделены. Диаграммообразующим элементом антенны является рефлектор, а роль источника первичного поля выполняет облучатель. В зависимости от требований, предъявляемых к антеннам, применяются различные типы рефлекторов: плоские и уголковые отражатели, параболоиды вращения, параболические цилиндры и др. Наиболее широкое распространение в системах радиосвязи получили антенны с рефлектором в виде параболоида. Введем основные определения. Раскрывом (апертурой) параболической антенны называется плоскость, опирающая на края зеркала (рис.4.1). Раскрыв параболоида вращения имеет форму круга. Фокусным расстоянием f параболического зеркала называется расстояние от фокуса до вершины зеркала. Фокальной осью называется прямая линия, проходящая через фокус и вершину зеркала. Углом раскрыва зеркала ψ0 называется угол, образованный фокальной осью и прямой, соединяющей фокус зеркала и край раскрыва.
Рис.4.1. Виды зеркал Параболой называется геометрическое место точек, равноудаленных от фокуса F и директрисы DD(FAn=AnBn, рис.4.2). Таким образом, основным свойством параболического зеркала является то, что сумма расстояний от фокуса до поверхности зеркала и от поверхности зеркала до раскрыва FAnCn является величиной постоянной при любых углах Поэтому, если в фокус параболического зеркала поместить источник сферических волн, то поверхность раскрыва становится синфазной поверхностью. Следовательно, антенна с параболическим рефлектором трансформирует сферическую волну в волну с плоским фронтом. При вращении параболы относительно фокальной оси Z образуется фигура в виде параболоида. В системе прямоугольных координат XYZ профиль параболического зеркала описывается формулой
x2=4fz (при y=0). (4.1)
Рис.4.2. Геометрические свойства параболы
плоским фронтом (плоскую волну). В соответствии с законами оптики все отраженные лучи от зеркала образуют семейство параллельных линий. При отсутствии расходящихся лучей ширина главного лепестка диаграммы направленности антенны оказывается равной нулю. В действительности ширина главного лепестка значительно отличается от нуля. Это объясняется тем, что приведенные рассуждения основаны на законах геометрической (лучевой) оптики и не учитывают дифракционные (волновые) процессы на краях зеркала, в принципе исключающие образование плоских волновых фронтов (принцип Гюйгенса–Френеля). Поэтому определение направленных свойств параболической антенны на основании законов геометрической оптики дает тем более точные результаты, чем больше размеры раскрыва антенны по отношению к длине волны. Благодаря этому краевые эффекты в меньшей мере влияют на лучевой механизм формирования излучаемой волны. В инженерной практике для простоты расчетов раскрыв параболической антенны принято считать синфазно возбужденной поверхностью, а излучаемую волну – плоской. Для расчета диаграммы направленности параболической антенны применяют метод, в основе которого лежит предположение, что источником вторичного излучения являются не токи проводимости, текущие по поверхности зеркала, а воображаемые источники поля (элементы Гюйгенса), расположенные в плоскости раскрыва, образующие сплошную решетку синфазных излучателей. Из курса «Электромагнитные поля и волны» известно, что плотность воображаемых поверхностных токов в раскрыве можно представить через характеристики поля в раскрыве, т.е. через векторы Е и Н. Направленные свойства параболической антенны зависят не только от ее относительных (относительно длины волны) размеров, но и от того, как распределена амплитуды поля по раскрыву. Наиболее высокие направленные свойства реализуются в том случае, когда амплитуда поля по раскрыву постоянна. Однако получить равномерное распределение амплитуды поля по раскрыву нереально. При возбуждении зеркала облучателем наведенные токи текут по вогнутой поверхности. Проекции линий тока на поверхность раскрыва (рис.4.3) представляют собой семейство кривых линий. Аналогичную картину в плоскости раскрыва образуют линии напряженности электрического поля. Как видно на рис.4.3, вектор напряженности электрического поля Е имеет две составляюшие – Ex и Ey, причем составляющие Ex на краях зеркала имеют максимальную амплитуду и диаметрально противоположны по знаку. Поэтому составляющая Ex вдоль фокальной оси не принимает участия в излучении, из-за чего излучающая способность периферии зеркала меньше, чем центральной области.
Рис.4.3. Картина поля в раскрыве параболы Уменьшение амплитуды поля от центра к краям раскрыва эквивалентно уменьшению его размера. Поэтому по сравнению с равноамплитудным распределением ширина главного лепестка диаграммы направленности (ДН) увеличивается. Уменьшить неравномерность поля в раскрыве можно за счет увеличения фокусного расстояния зеркала. Однако при этом уменьшается доля энергии облучателя, падающей на зеркало, так как увеличивается «переливание» энергии через край зеркала. Распределение амплитуды поля по раскрыву зеркала зависит также от направленных свойств облучателя. Чем шире его диаграмма направленности, тем более равномерно поле в раскрыве. При этом неизбежно уменьшается доля энергии, падающая на зеркало. Соответственно, из-за дифракционных эффектов на краю зеркала увеличивается уровень боковых лепестков ДН антенны. Все вышеизложенное показывает, что при заданном диаметре зеркала для получения максимально узкого главного лепестка ДН нужно применять антенны с большим фокусным расстоянием и ненаправленным облучателем. А для получения максимального КНД при заданном размере раскрыва необходимо обеспечить определенное соотношение между фокусным расстоянием зеркала и ДН облучателя. Таким образом, условие максимально узкого главного лепестка ДН антенны и максимального коэффициента направленного действия (КНД) различаются. Поэтому на практике применяются как длиннофокусные антенны (условие максимально узкого лепестка ДН), так и короткофокусные антенны (условие максимального КНД). Длиннофокусные антенны применяют тогда, когда необходима высокая разрешающая способность антенны (в радиоастрономии, радиолокации, в системах наведения), а короткофокусные антенны чаще всего применяют как приемные при работе с сигналами малого уровня мощности (космическая радиосвязь и др.) В качестве облучателя зеркальных антенн обычно применяют слабонаправленные антенны (антенны относительно малых размеров): рупоры, спирали, щелевые излучатели, вибраторы с рефлектором. Диаграмма направленности таких облучателей достаточно хорошо аппроксимируется функцией
F(φ)=cosφn. (4.2)
Аналитически показано, что, если ДН однонаправленного облучателя (при n=1) имеет осевую симметрию (является фигурой вращения), то максимальный КНД антенны принимает максимальное значение, если амплитуда напряженности поля на краю зеркала относительно амплитуды поля у его вершины составляет 0.316 (-10 дБ по мощности). Формулы для расчета диаграммы направленности имеют достаточно громоздкий вид. В первом приближении, полагая, что поле в раскрыве синфазно и имеет постоянную амплитуду по раскрыву, диаграмму направленности антенны можно вычислять по формуле
где J1 – функция Бесселя первого рода первого порядка от аргумента u=kRsinφ, R – радиус раскрыва. Реальные распределения амплитуды поля по раскрыву не имеют строгого аналитического выражения и часто аппроксимируются выражением
где - Соответственно, ДН антенны рассчитывается по формуле
Здесь F1(φ)-ДН элемента Гюйгенса, Fc(φ)- множитель системы:
Fc(φ)= Δ где: J1 и J2 функции Бесселя первого рода первого и второго порядка, Множитель, определяющий ДН элемента Гюйгенса при расчетах ДН антенны обычно не учитывают из-за его слабого влияния на ДН антенны. Коэффициент направленного действия параболической антенны определяется по формуле для плоских синфазных поверхностей
где S – площадь раскрыва, ν (КИП) – коэффициент использования поверхности раскрыва:
ν= где Sэфф – эффективная площадь раскрыва антенны. Эффективной (действующей) площадью раскрыва антенны Sэфф называется площадь синфазной и равноамплитудной излучающей поверхности, при условии одинаковой излучаемой ими мощности. Результирующий КИП приближенно можно представить произведением двух основных множителей
ν=ν1ν2, (4.9)
где ν1 - апертурный КИП, ν2 - коэффициент «перехвата». Апертурный КИП зависит от закона распределения амплитуды поля в раскрыве зеркала. Коэффициент перехвата определяется направленными свойствами облучателя и размерами зеркала и определяет долю мощности облучателя, падающую на зеркало в пределах его угла раскрыва. Иными словами, коэффициент перехвата позволяет определить неиспользуемую часть мощности облучателя за счет «переливания» энергии через край зеркала. Коэффициент направленного действия параболической антенны можно вычислять по приближенной формуле
где 2φ Поляризация волны, излучаемой параболической антенной, зависит от поляризационных свойств облучателя. Антенна с облучателем в виде симметричного вибратора излучает линейно-поляризованную волну. Вектор Е волны с осью вибратора находится в одной плоскости. Эта плоскость называется плоскостью поляризации волны. Параболическая антенна со спиральным облучателем излучает волну с круговой поляризацией. Вектор Е излучаемой волны в этом случае в течение одного периода высокой частоты делает полный оборот в плоскости, нормальной направлению распространения. При этом конец вектора Е при вращении описывает замкнутую кривую в виде круга. Реально кривая имеет форму эллипса. Отношение малой полуоси эллипса к большой полуоси называется коэффициентом равномерности поляризационного эллипса. В случае линейной поляризации коэффициент равномерности равен нулю, в случае круговой – единице.
|


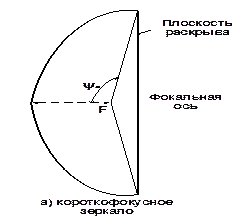
 в пределах угла раскрыва.
в пределах угла раскрыва.

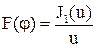 , (4.3)
, (4.3) , (4.4)
, (4.4)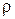 – расстояние от фокуса до текущей точки на поверхности зеркала, Δ(«пъедестал») – отношение амплитуды напряженности поля на краю зеркала к амплитуде поля в центре.
– расстояние от фокуса до текущей точки на поверхности зеркала, Δ(«пъедестал») – отношение амплитуды напряженности поля на краю зеркала к амплитуде поля в центре. . (4.5)
. (4.5) , (4.6)
, (4.6)
 , (4.7)
, (4.7) , (4.8)
, (4.8) , (4.10)
, (4.10) и 2θ
и 2θ 


