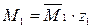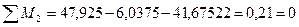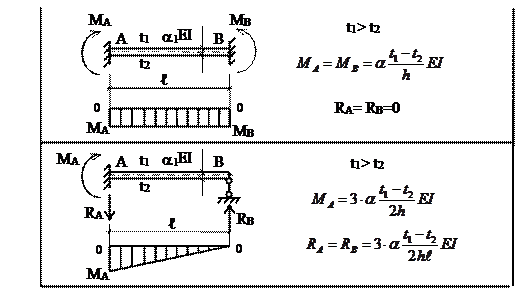Запоріжжя
Міністерство освіти і науки України Запорізька державна інженерна академія
БУДІВЕЛЬНА МЕХАНІКА Методичні вказівки Розрахунок кінематично невизначуваних рам методом переміщень
для студентів ЗДІА денної і заочної форми навчання спеціальностей 7.09.2101 «Промислове та цивільне будівництво» 7.09.2103 «Міське будівництво та господарство»
Рекомендовано до видання на засіданні кафедри ПБМ протокол №16 від 14.06.07
Будівельна механіка. Методичні вказівки. Розрахунок кінематично невизначуваних рам методом переміщень для студентів ЗДІА спеціальностей «Промислове та цивільне будівництво», «Міське будівництво та господарство»/Укл.: В. Я. Танцура, А. А. Бобраков. – Запоріжжя: видавництво ЗДІА, 2008. 33 с.
Укладачі: В. Я. Танцура, ст. викладач А. А. Бобраков, асистент
Відповідальний за випуск: зав. Кафедрою ПБМ к.т.н., проф. В. С. Гавриш
Розрахунок кінематично невизначуваних рам методом переміщень 1. Загальні відомості та припущення методу переміщень. Розрахунок споруд на міцність та жорсткість можливо виконувати двома шляхами: а) спочатку знайти внутрішні зусилля та напруження в елементах споруди (напружений стан), а потім знайти деформації та переміщення вузлів та елементів споруди (деформований стан); б) спочатку знайти деформований стан споруди, а потім, враховуючи закон Гука, знайти напружений стан. Перший розрахунок виконується методом сил, другий – методом переміщень. Метод переміщень є одним із найрозповсюдженіших методів розрахунку стержневих кінематично невизначуваних систем. Він є основним при розрахунку рам на стійкість та динамічне навантаження, покладен в основу деяких наближених методів розрахунку, використовується при розрахунку методом скінчених елементів. В багатьох випадках застосування методу переміщень призводить до меншої трудомісткості обчислювальних робіт, ніж метод сил. Метод переміщень ґрунтується на спрощуючих припущеннях. а) Кути між стержнями, які збігаються у жорсткому вузлі, не змінюються після деформування споруди, тобто стержні в жорсткому вузлі повертаються на однаковий кут. б) Деформаціям від поперечних і поздовжніх сил можно знехтувати. в) Не береться до уваги зближення кінців стержня в наслідок його згину. г) Кути повороту стержнів мали і тому їх тангенси і синуси равним цим кутам.
2. Ступень кінематичної невизначуваності системи. Ступенем кінематичної невизначуваності (СКН) системи будемо називати кількість незалежних кутових та лінійних переміщень вузлів системи, знання яких дозволить побудувати деформований стан цієї системи: СКН = n де n n Кількість n
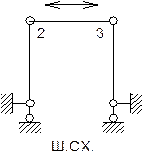
Ця формула використовується не для заданої схеми рами, а для шарнірної схеми (ш.сх), яка утворюється постановкою шарнірів в жорсткі вузли та жорсткі закріплення. У – число вузлів, С – число стержнів, С Наприклад:
CKH =1 + 1 = 2 Рис. 1
Ш.СХ.
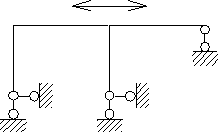
CKH =2 + 1 = 3 Рис. 2 3. Основна система методу переміщень. Знайшовши ступень кінематичної невизначуваності системи, другим кроком утворюють основу систему метода переміщень. Як відомо, переміщення вузлів бувають двох типів: кутові та лінійна. Основна система утворюється з вихідної введенням в її вузли додаткових в’язей також двох типів: 1) Для запобігання повороту всіх жорстких вузлів до них вставляються рухомі (плаваючі) затиснення. Це такі умовні в’язи, які усувають тільки повороти вузлів, але не усувають їх поступальні переміщення. У таких затисненнях виникає лише одна реакція – момент. Жорсткими вузлами є місця, де: - з’єднуються без шарнірів два або більше стержнів; - змінюється під кутом напрям осі стержня; - до стержня приєднується за допомогою прилеглого шарніра стержень або кілька стержнів; - ступінчато змінюється жорсткість стержня. 2) Можливі поступальні переміщення вузлів системи виключаються встановленням додаткових опорних стержнів по напряму можливого переміщення. У таких опорних стержнях виникає реакція спрямована вздовж стержня. Слід зауважити, що основна система методу переміщень – одна єдина для заданої системи, що спрощує розрахунок. Також встановлювання додаткових в’язів дозволяє розглядати основу систему як систему окремих балок с двома жорсткими опорами, або с жорсткої і шарнірної опорами. Розрахунок цих балок на дію зовнішнього навантаження та кутові і поступальні переміщення опор виконується заздалегідь. Визначаються опорні моменти і реакції, будуються епюри згинаючих моментів і ці данні наводяться у таблицях (див. додаток 1 і 2).
4. Канонічні рівняння методу переміщень. Додаткові в’язи, встановлені при утворенні основної системи, виключають кути повороту жорстких вузлів та поступальні переміщення вузлів системи. Ці переміщення і є основними невідомими метода переміщень. Вони позначаються літерами Для еквівалентності заданої і основної систем необхідно, щоб реакції в додаткових в’язах дорівнювались нулю. Ця обставина використовується для складення системи розв`язувальних рівнянь. Ці рівняння утворюють систему лінійних алгебраїчних рівнянь відносно невідомих переміщень, яким перешкоджають накладені додаткові в’язи, і в канонічній формі при СКН=n мають вигляд
Тут:
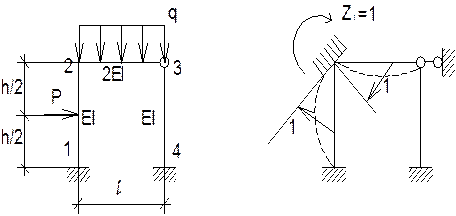
5. Визначення коефіцієнтів та вільних членів канонічних рівнянь. Для визначення коефіцієнтів та вільних членів канонічних рівнянь (3) необхідно побудувати окремо епюри згинаючих моментів та визначити реакціїї в основній системі від дії одиничних значень невідомих Наприклад (див рис.3).
Рис 4
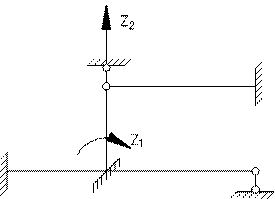
Використаємо статичний метод. Для знаходження коефіціентів Пунктіром визначені розтягнуті волокна стержня.
Рис. 5
Для знаходження коефіцієнтів
Рис. 6
При обчислюванні коефіціентів можно користуватись теоремою про взаімність реакцій
6. Перевірка розрахунку коефіцієнтів і вільних членів канонічних рівнянь. Використовуючи інтегральну формулу Мора і множення епюр згинальних моментів по правилу Веріщагіна можно перевірити коефіцієнти канонічних рівнянь.
Вільні члени перевіряються за формулою
де Коефіцієнти і вільні члени можно перевіряти разом. Для цього спочатку треба побудувати в основній системі епюру згинальних моментів
Построчна перевірка коефіціентів кожного канонічного рівняння, наприклад і-ого:
При правильному визначенні коефіціентів ця сума повинна получитися при множенні епюр
Універсальна перевірка усіх коефіцієнтів канонічних рівнянь: Ця сума повинна получитися при множенні епюри
Постолбцова перевірка всіх вільних членів виконується за формулами:
7. Побудова дійсних епюр згинаючих моментів, поперечних та продовжніх сил, іх перевірки. Підставляємо знайдені та перевірені коефіцієнти та вільні члени до системи канонічних рівнянь, розв`язуємо їх, отримуємо дійсні величини основних невідомих Дійсна епюра згинаючих моментів будується способом накладення епюр відповідно до формули
Тут Основною перевіркою дійсної епюри згинальних моментів є статична перевірка, яка полягає в перевірці умов рівноваги всіх вузлів рами. Для її виконання почергово відокремлюються всі проміжні вузли, до яких прикладаються зовнішні вузлові навантаження, після чого перевіряється, чи дорівнює нулю сума моментів у даному вузлі. При цьому відносна похибка не повинна перевищувати 1%. Можно робити кінематичну перевірку епюри згинаючих моментів, яка полягає в обчисленні переміщень, які завідомо дорівнюються нулю. Необхідно задану статично невизначувану схему рами змінити статично визначуваною, тобто перейти до основної системи методу сил, відкинувши «зайві» в’язі. Для кінематичної перевірки слід побудувати епюри згинаючих моментів у статично визначуваній основній системі від окремих одиничних невідомих Переміщення обчислюються по формулам
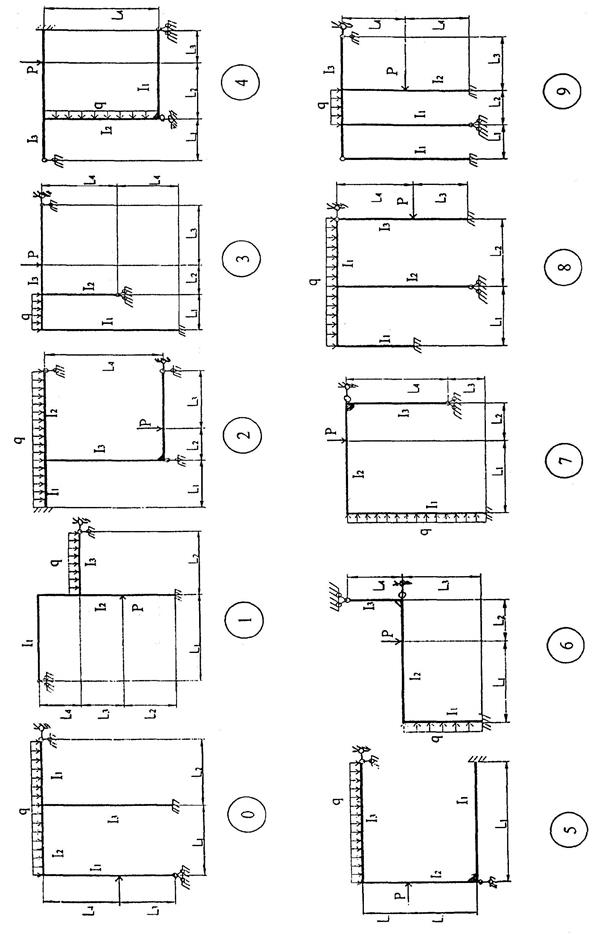
Відносна похибка також не повинна перевищувати 1%. Епюра поперечних сил будується користуючись диференціальною залежністю між дійсними поперечними силами Q та згинаючими моментами. Розрахунок виконується для кожного стержня рами. Поздовжні сили обчислюємо, розглядаючи послідовно рівновагу вузлів рами. Вузли необхідно розглядати в такій послідовності, щоб у кожному з них було не більше двох невідомих поздовжніх сил. Вирізавши вузол, прикладаємо до нього вже відомі поперечні сили, що беруться з епюри Q, і поздовжні сили, які спрямовуємо в додатному непрямі, тобто вважаємо ці сили розтягуючими. Використовуючи рівняння рівноваги на координатні вісі, знайдемо невідомі поздовжні сили. Провівши переріз, що відокремлює раму від опор і приклавши в місцях перерізів згинальні моменти, поперечні і поздовжні сили, перевіряємо виконання умов рівноваги всієї системи вцілому. 8. Вибор завдання для самостійного розрахунку та зміст розрахунко-графічної роботи “Розрахунок кінематично невизначених рам методом переміщень”. По індивідуальному шифру кожен студент із таблиці 1 і рис 1 вибирає вихідні дані для розрахунку рами методом переміщень. Зміст завдання 1. Визначити ступень кінематичної невизначуваності рами, обрати основну систему та записати канонічні рівняння. 2. Побудувати в основній системі епюри згинаючих моментів від дії одиничних переміщень і від заданного навантаження. 3. Визначити коефіцієнти і вільні члени канонічних рівнянь та виконати їх перевірку. 4. Визначити невідомі переміщення, перевірити їх розрахунок. 5. Побудувати епюру згинаючих моментів, виконати статичну та кінематичну перевірки цієї епюри. 6. Побудувати епюрі поперечних і поздовжніх сил та виконати перевірки цих епюр.
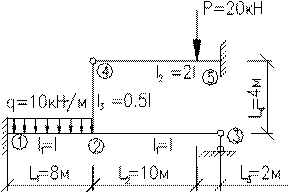
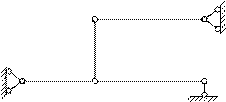
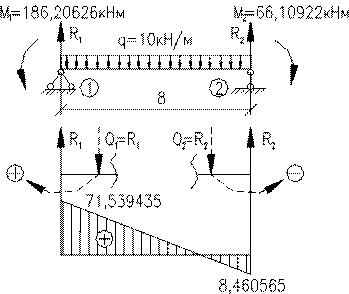
Розрахунок 2 статично невизначеної смужкою рами методом переміщень Вихідні дані: L1= 8 м; L2= 10 м; q=10 кН/м; I1= I; L3= 2 м; L4= 4 м;
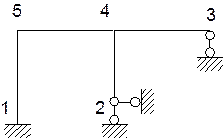
СКН = nу + nл = 1 + 1 = 2 nу = 1 (вузел 2) nл = 2 · У – С – С0 = 2 · 5 – 4 – (2 + 2 + 1) = 1 (за шарнірною схемою)
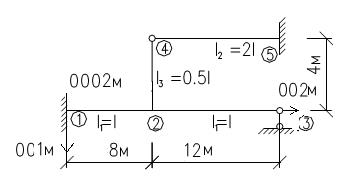
Шарнірна схема Основна система
Будуємо епюру згинаючих моментів при
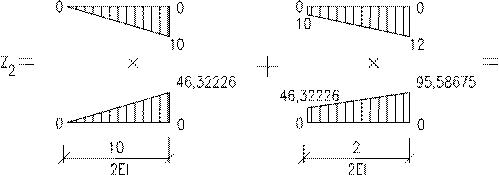
Будуємо епюру згинаючих моментів
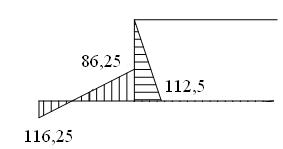
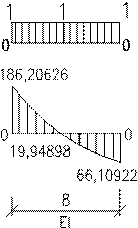
Будуємо епюру згинаючих моментів від дії зовнішнього навантаження
Визначаємо значення коефіцієнтів і вільних членів канонічних рівнянь. Вирізаємо вузол 2 ( з
з
Вирізаємо стрижень 2 – 4 (по
з М1
з М2
з Мр
Перевірка: I. 1) 2)
II. 1)
Перевірка виконується. Підставимо значення вільних члені у канонічне рівняння.
Вирішуючи систему, отримуємо:
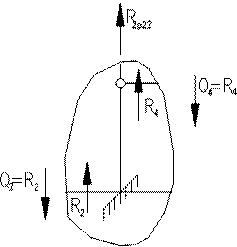
Перевірка (рівновага вузла 2)
Визначення переміщень
Основна система метода сил
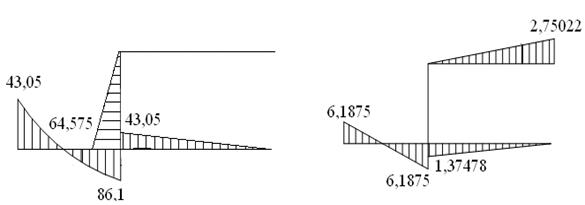
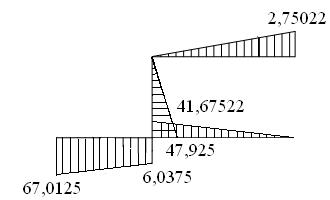
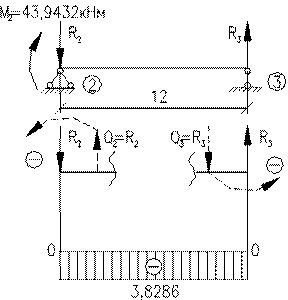
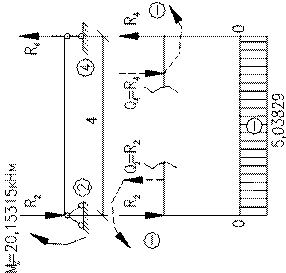
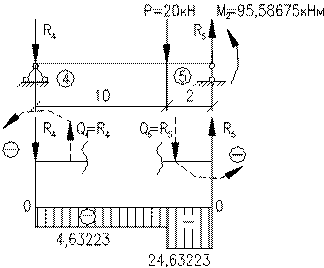
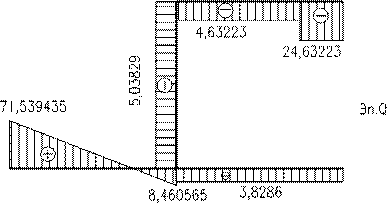
Будуємо епюру поперечних зусиль
Будуємо епюри подовжніх зусиль N1
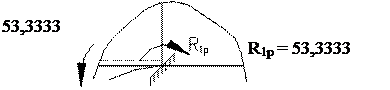
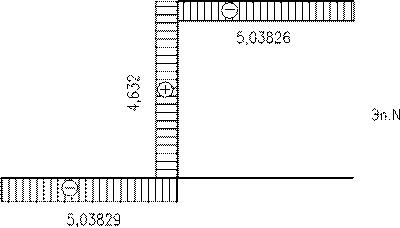
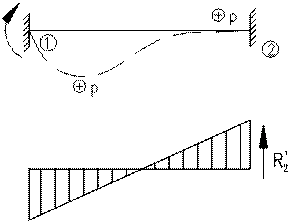
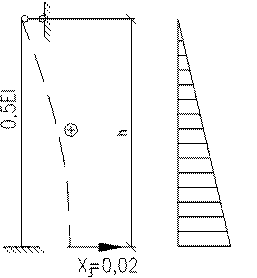
Побудування епюри згинаючих моментів при зміщенні опор
Основна система
Канонічні рівняння мають вид:
r11=1.125EI r12= r21= 0.07292EI r22=0,19271EI
j1=0,002
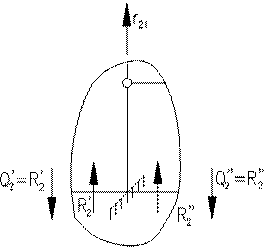
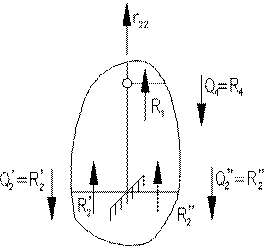
Вирізаємо вузол 2 (де
Вирізаємо стрижень 2-4 (по
0,07292
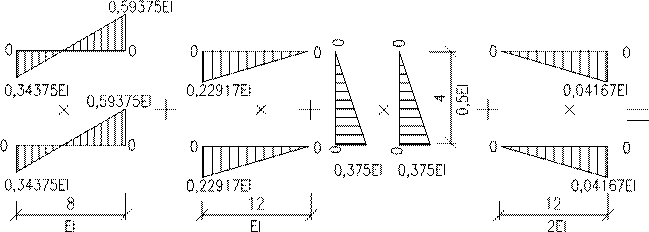
Помножимо всі значення епюр на EI
Перевірка
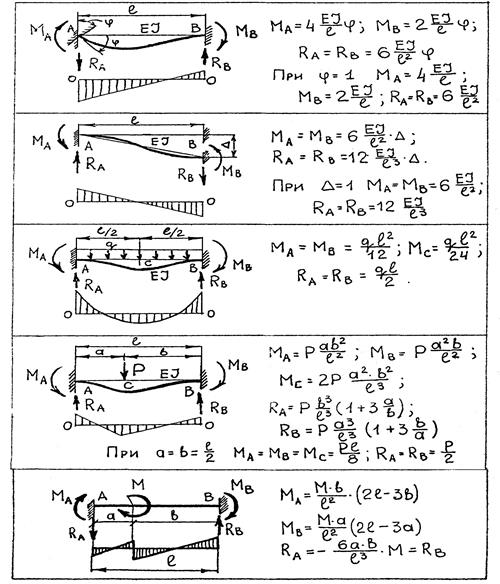
Додаток 1 Однопрогонова балка з двома жорсткими опорами. Реакції і моменти при дії зовнішнього навантаження та переміщення опор.
Додаток 2 Однопрогонова балка з жорсткой і шарнірно-рухомой опорами. Реакції і моменти при дії зовнішнього навантаження та переміщення опор.
Література
1. Бутенко Ю.И. и др. Строительная механика стержневых систем и оболочек. – К.: Высш. шк., 1980. -488с 2. Строительная механика. Руководство к практическим занятиям / Под ред. Ю.И. Бутенко. – К.: Высш. шк., 1989. -367с 3. Руководство к практическим занятиям по курсу строительной механики (статика стержневых систем) / Под ред. Г.К. Клейна. – М.: Высш. шк., 1980. -384с 4. Баженов В.А., Іванченко Г.М., Шишов О.В. Будівельна механіка. Навч. посібник. – К.: Каравела, 2006. – 344с 5. Танцура В.Я., Сафонова Л.Е. Строительная механика. Методические указания у выполнению курсовой работы “Расчет статически неопределимых плоских ферм методом перемещений”. – Запорожье: ЗИИ, 1985. -24с
|

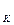 + n
+ n 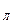 (1)
(1)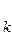 - кількість незалежних кутових переміщень жорстких вузлів системи,
- кількість незалежних кутових переміщень жорстких вузлів системи,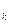 дорівнюється кількості жорстких вузлів рам (Не враховуються жорсткі закріплення). Кількість n
дорівнюється кількості жорстких вузлів рам (Не враховуються жорсткі закріплення). Кількість n 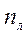 =2У-С-С
=2У-С-С  ……………………………(2)
……………………………(2)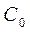 =1, шарнірно – нерухома опора -
=1, шарнірно – нерухома опора - 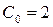 , жорстке закріплення -
, жорстке закріплення -  .
.
 1)
1)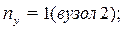
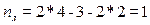
 2)
2)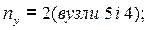
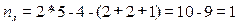
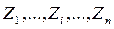 при СКН=n. Напрям дії переміщення вибирає рахівник, при цьому, якщо результат має знак «+», то дійсний напрям переміщення вибраний правильно, якщо знак «-», то дійсний напрям переміщення протилежний вибраному.
при СКН=n. Напрям дії переміщення вибирає рахівник, при цьому, якщо результат має знак «+», то дійсний напрям переміщення вибраний правильно, якщо знак «-», то дійсний напрям переміщення протилежний вибраному.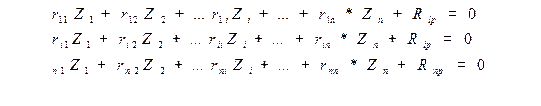 (3)
(3)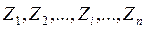 - основні невідомі методу переміщень,
- основні невідомі методу переміщень,  - коєфіцієнт – реакція (момент у рухомому затисненні або реакція у додатковому стержні) у додатковій в`язі «і» основної системи від примусового переміщення
- коєфіцієнт – реакція (момент у рухомому затисненні або реакція у додатковому стержні) у додатковій в`язі «і» основної системи від примусового переміщення 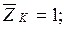
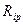 - вільний член – реакція (момент чи сила) в накладеній в`язі «і» від зовнішнього навантаження.
- вільний член – реакція (момент чи сила) в накладеній в`язі «і» від зовнішнього навантаження.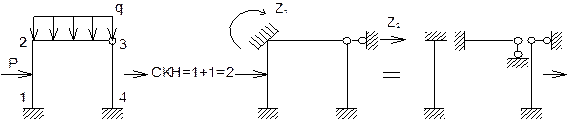 Наприклад (див. рис.1):
Наприклад (див. рис.1):
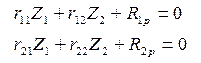 основна система Рис 3.
основна система Рис 3.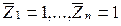 і від дії зовнішнього навантаження. Побудова одиничних і вантажної епюр здійснюється за допомогою таблиць однопрогонових балок (додаток 1,2).
і від дії зовнішнього навантаження. Побудова одиничних і вантажної епюр здійснюється за допомогою таблиць однопрогонових балок (додаток 1,2).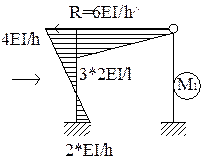
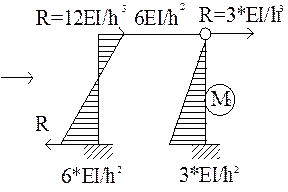


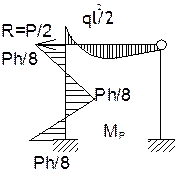
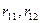 і вільного члена
і вільного члена 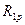 вирізаємо вузол 2 (де
вирізаємо вузол 2 (де 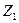 ) з усіх епюр і використовуєм умови рівноваги вузла:
) з усіх епюр і використовуєм умови рівноваги вузла:
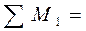 -
- 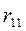 +
+ 


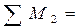 -
- 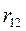 -
- 
 -6
-6 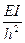

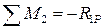 +
+ 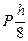 -
- 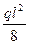
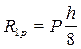 -
- 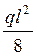
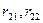 і вільного члена
і вільного члена 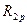 треба вирізати стержень основної системи, поступальному переміщенню якого заважає додатковий опорний стержень. При цьому будемо використовувати рівняння рівноваги усіх сил на вісь х. В перерізаних стояках 1-2 и 3-4 виникають поперечні сили, які по модулю рівні реакціям, але протилежні по напряму
треба вирізати стержень основної системи, поступальному переміщенню якого заважає додатковий опорний стержень. При цьому будемо використовувати рівняння рівноваги усіх сил на вісь х. В перерізаних стояках 1-2 и 3-4 виникають поперечні сили, які по модулю рівні реакціям, але протилежні по напряму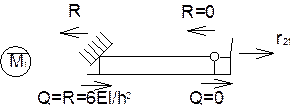

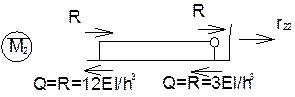
 -15
-15 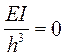
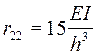

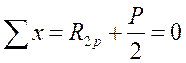
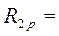 -
- 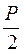
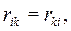 у прикладі
у прикладі 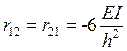
 (4)
(4)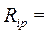

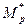 - епюра згинаючих моментів від дії заданого навантаження, побудованая для статично визначуваної схеми системи, полученої від заданої невизначеної, тобто перейти до основної системи методу сил, відкинувши «зайві» в`язі.
- епюра згинаючих моментів від дії заданого навантаження, побудованая для статично визначуваної схеми системи, полученої від заданої невизначеної, тобто перейти до основної системи методу сил, відкинувши «зайві» в`язі. при одночасній дії всіх одиничних переміщень
при одночасній дії всіх одиничних переміщень 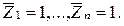
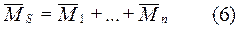
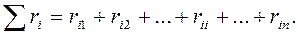
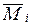 та
та 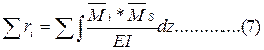
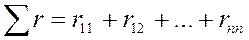 .
. на саму себе, тобто
на саму себе, тобто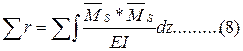
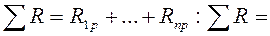 -
- 
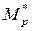 дивись формулу (5).
дивись формулу (5).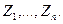 Обов’язково перевіряємо обчислені величини основних невідомих, підставивши їх у кожне канонічне рівняння або у сумарне рівняння.
Обов’язково перевіряємо обчислені величини основних невідомих, підставивши їх у кожне канонічне рівняння або у сумарне рівняння.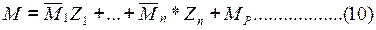
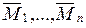 - епюри згинаючих моментів в основній системі від одиничних примусових переміщень
- епюри згинаючих моментів в основній системі від одиничних примусових переміщень 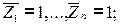
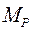 - епюра згинаючих моментів в основній системі від зовнішнього навантаження;
- епюра згинаючих моментів в основній системі від зовнішнього навантаження; 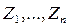 - дійсні величини основних невідомих.
- дійсні величини основних невідомих.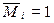 методу сил або від сукупності усіх невідомих метод сил
методу сил або від сукупності усіх невідомих метод сил 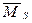 .
.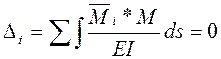 або
або 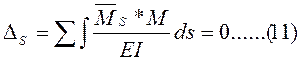

 Канонічні рівняння мають вид:
Канонічні рівняння мають вид: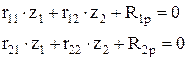
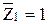 .
.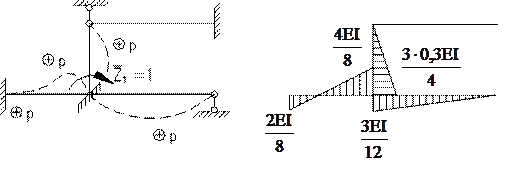

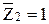 .
.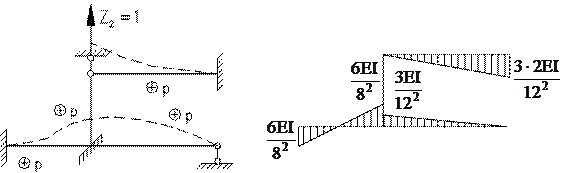

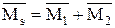
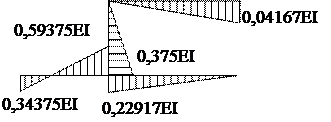
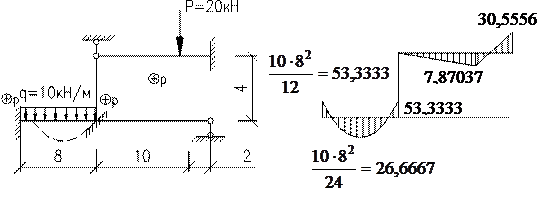

 )
) з
з 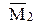
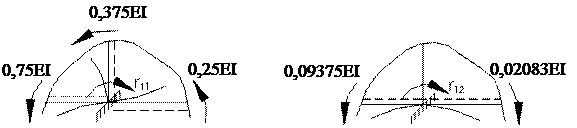
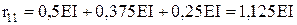
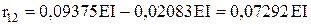
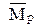
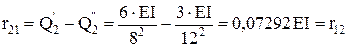
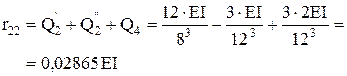
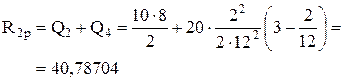
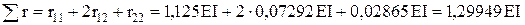
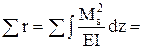
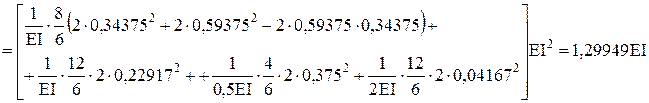
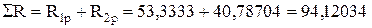
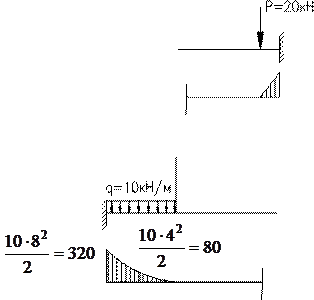 М*р
М*р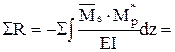
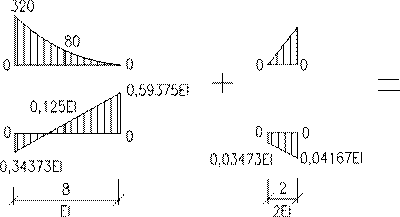
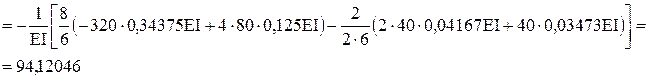
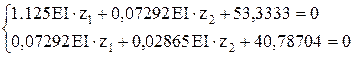
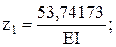
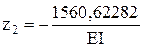

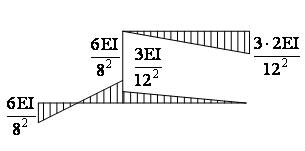
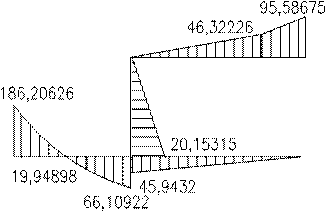 Эп. М
Эп. М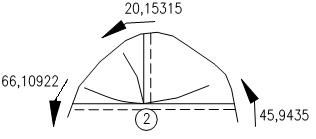

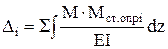
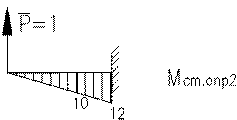
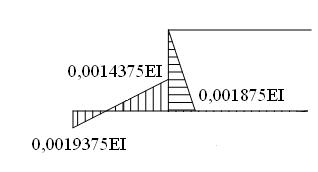
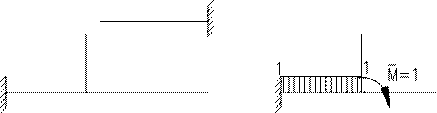 Мст.опр1
Мст.опр1
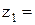
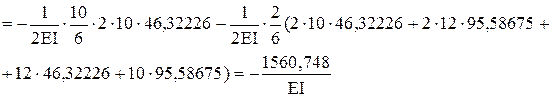

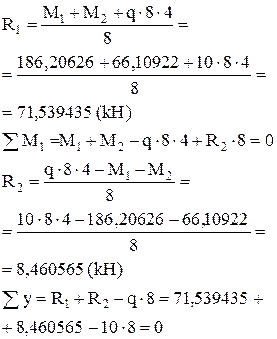



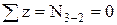
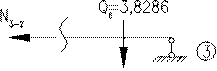
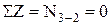

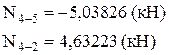
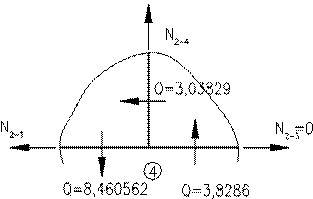

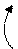
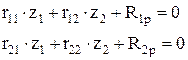

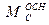
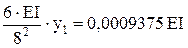
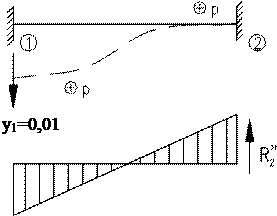
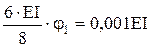
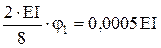
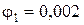

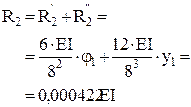
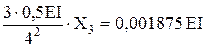
 ) з
) з 
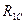 =0,001875EI+0,0014375EI=0,0033125EI
=0,001875EI+0,0014375EI=0,0033125EI ) з
) з 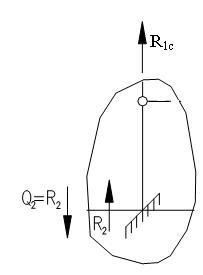
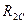 =
= 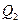 =0,006422EI
=0,006422EI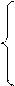 1,125
1,125 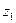 + 0,0792
+ 0,0792 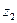 + 0,0033125 = 0
+ 0,0033125 = 0