Свойства корня n-ой степениСначала перечислим основные свойства корней n-ой степени: 1. свойство корня из произведения двух неотрицательных чисел a и b, ему отвечает равенство 2. корень из дроби обладает следующим свойством 3. при любом действительном a и четных показателях n=2·m справедливо 4. свойство корня из корня 5. для любого неотрицательного a и произвольных натуральных n и m справедливо равенство 6. свойство корня степени n из степени неотрицательного числа a в натуральной степени m, определяемое равенством 7. свойство сравнения корней с одинаковым показателем: для любых положительных чисел a и b таких, что a<b, выполняется неравенство 8. свойство сравнения корней с одинаковыми подкоренными числами: если m и n такие натуральные числа, что m>n, тогда при 0<a<1 справедливо неравенство Все записанные равенства остаются справедливыми, если в них поменять местами левую и правую части. В таком виде они употребляются также часто, в основном при упрощении и преобразовании выражений.
2. Степени и их свойства. Степенью называется выражение вида:
|
, это свойство распространяется на произведение k неотрицательных чисел a1, a2, …, ak как 
;
, где a – любое неотрицательное действительное число, а b – положительное действительное число;
, а при нечетных n=2·m−1 выполняется равенство 
.
, где a – любое неотрицательное число, n и m – натуральные числа, это свойство можно распространить как 
;
;
;
;
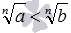, а при a>1 выполняется 
.
, где:
— основание степени;
— показатель степени.
