Свойства постоянной функции.
· Область определения: все множество действительных чисел. · Постоянная функция является четной. · Область значений: множество, состоящее из единственного числа С. · Постоянная функция невозрастающая и неубывающая (на то она и постоянная). · Говорить о выпуклости и вогнутости постоянной не имеет смысла. · Асимптот нет. · Функция проходит через точку (0,C) координатной плоскости
5. Показательная функция и её свойства Функция вида . Свойства показательной функции
6. Степенная функция и её свойства. Степенна́я фу́нкция — функция Свойства[править | править вики-текст] См. также: Возведение в степень · Функция непрерывна и неограниченно дифференцируема во всех точках, в окрестности которых она определена. Нуль, вообще говоря, является особой точкой; например, функция · В интервале · Производная функции: · Неопределённый интеграл: · Если · При
7. Логарифмическая функция и её свойства. Функцию, заданную формулой y=logax, называют логарифмической функцией с основанием a. (a>0,a≠1)
Основные свойства логарифмической функции: 1. Область определения логарифмической функции - множество всех положительных чисел. D(f)=(0;+∞);
2. Множество значений логарифмической функции - множество R всех действительных чисел. E(f)=(−∞;+∞);
3. Логарифмическая функция на всей области определения возрастает при a>1 или убывает при 0<a<1.
8. Элементы комбинаторики. Рассмотрим некоторое множество Х, состоящее из n элементов Размещением из n элементов множества Х по k элементам назовем любой упорядоченный набор Если выбор элементов множества Если же выбор делается без возвращения, т.е. каждый элемент множества Х можно выбирать только один раз, то количество размещений из n по k обозначается Пример. Пусть даны шесть цифр: 1; 2; 3; 4; 5; 6. Определить сколько трехзначных чисел можно составить из этих цифр. Решение. Если цифры могут повторяться, то количество трехзначных чисел будет
9. Основы тригонометрии. ОСНОВЫ ТРИГОНОМЕТРИИ 1. Основные понятия тригонометрии 1.1. Отношения в прямоугольном треугольнике Пусть ∆ABC – прямоугольный, угол С – прямой, угол B – острый, a и b – катеты, с – гипотенуза (рисунок 1.1). Синус угла B равен отношению противолежащего этому углу катета к гипотенузе: c b sin B =, косинус угла B равен отношению прилежащего катета к гипотенузе: c a cos B =, тангенс угла B равен отношению противолежащего и прилежащего катетов: a b tgB =, котангенс угла B равен отношению прилежащего и противолежащего катетов: b a ctgB =. Рисунок 1.1. Прямоугольный треугольник ABC, a и b – катеты, с – гипотенуза 1.2. Тригонометрическая окружность. Синус, косинус, тангенс и котангенс угла α. Периодичность значений синуса, косинуса, тангенса и котангенса угла α Тригонометрическая (единичная) окружность – окружность радиусом, равным одному и с центром в начале координат (рисунок 1.2). Луч OPα получен поворотом против часовой стрелки луча OP0 на угол α. Ордината точки Pα – синус угла α (sinα), абсцисса точки Pα – косинус угла α (cosα). Отрезок [-1;1] на оси Оy – линия синусов, отрезок [-1;1] на оси Оx – линия 4 косинусов. Величина α α = cos sec 1 – секанс угла α, величина α α = sin cosec 1 – косеканс угла α. Тангенс угла α – это α α α = cos sin tg, котангенс угла α – это α α α = sin cos ctg. Прямая x=1 – линия (ось) тангенсов, прямая y=1 – линия (ось) котангенсов. Рисунок 1.2. Тригонометрическая окружность Угол α может измеряться в градусах и в радианах. Угол в один радиан – центральный угол, длина дуги которого равна радиусу окружности 1 рад≈ 570 17’. Формула перевода градусной меры угла α в радианную 0 0 180 α⋅π α =, где 0 α – градусная мера угла. Значения синуса косинуса и тангенса периодически повторяются: sin(α + 2πk) = sinα, cos(α + 2πk) = cosα, tg(α+ πk) = tgα, ctg(α + πk) = ctgα, где k ∈Z. 10. Аксиомы стереометрии и следствия из них. Основные фигуры в пространстве: точки, прямые и плоскости.
Основные свойства точек, прямых и плоскостей, касающиеся их взаимного расположения, выражены в аксиомах. А1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
А2. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости
Замечание. Если прямая и плоскость имеют только одну общую точку, то говорят, что они пересекаются.
А3. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
Следствие 1. Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна. Следствие 2. Через две пересекающиеся прямые проходит плоскость, и притом только одна.
11. Взаимное расположение прямых в пространстве. Возможны ТРИ случая взаимного расположения двух прямых в пространстве: Определение 1. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются. Определение 2. Прямые, которые не пересекаются и не лежат в одной плоскости, называются скрещивающимися. Определение 3. Прямые, которые пересекаются и не лежат в одной плоскости, называются пересекающимися. 12. Взаимное расположение прямой и плоскости в пространстве.
13. Взаимное расположение плоскостей. Две различные прямые на плоскости или параллельны, или пересекаются. Точно так же две различные плоскости в пространстве либо параллельны, либо пересекаются Плоскости параллельны Плоскости пересекаются 14. Цилиндр. Цилиндр это тело, ограниченное цилиндрической поверхностью с замкнутой направляющей и двумя параллельными плоскостями. 15. Конус. Геометрическое тело, образуемое вращением прямоугольного треугольника вокруг катета 16. Шар. Шар — геометрическое тело, ограниченное сферической или шаровой поверхностью. 17. Пирамида. Пирами́да — многогранник, одна из граней которого (называемая основанием) — произвольный многоугольник, а остальные грани (называемые боковыми гранями) — треугольники, имеющие общую вершину. По числу углов основания различают пирамиды треугольные (тетраэдр), четырёхугольные и т. д. Пирамида является частным случаем конуса
18. Призма. Призма — многогранник, две грани которого являются равными многоугольниками, лежащими в параллельных плоскостях, а остальные грани —параллелограммами, имеющими общие стороны с этими многоугольниками. Эти параллелограммы называются боковыми гранями призмы, а оставшиеся два многоугольника называются ее основаниями
19. Понятие многогранника. Правильные многогранники. Правильный многогранник — это выпуклый многогранник, состоящий из одинаковых правильных многоугольников и обладающий пространственной симметрией. Многогранник называется правильным, если: 1. он выпуклый; 2. все его грани являются равными правильными многоугольниками; 3. в каждой его вершине сходится одинаковое число рёбер.
20. Понятие вектора в пространстве и действия над ними. Основные определения и обозначения для векторов в пространстве вводятся так же, как и для векторов на плоскости. Вектором называется отрезок, для которого указано, какой из его концов считается началом, а какой - концом. Любая точка пространства рассматривается как нулевой вектор.
Примерный план ответа: Алгебра. 1. Определение понятия, его обозначение, пример. 2. Формулировка свойств, правил (без вывода), их запись с помощью условных обозначений, примеры. Геометрия. 1.Определение понятия, его изображение, основные элементы. 2.Формулы для вычисления площади поверхности и объёма.
|

 называется показательной функцией
называется показательной функцией



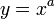 , где
, где  (показатель степени) — некоторое вещественное число[1]. К степенным часто относят и функцию вида
(показатель степени) — некоторое вещественное число[1]. К степенным часто относят и функцию вида  , где k — некоторый масштабный множитель.[2] Существует также комплексное обобщение степенной функции. На практике показатель степени почти всегда являетсяцелым или рациональным числом.
, где k — некоторый масштабный множитель.[2] Существует также комплексное обобщение степенной функции. На практике показатель степени почти всегда являетсяцелым или рациональным числом. определена в нуле и его правой окрестности, но её производная
определена в нуле и его правой окрестности, но её производная  в нуле не определена.
в нуле не определена. функция монотонно возрастает при
функция монотонно возрастает при  и монотонно убывает при
и монотонно убывает при  Значения функции в этом интервале положительны.
Значения функции в этом интервале положительны.
 , то
, то 
 получаем:
получаем: 


 . Будем выбирать из этого множества различные упорядоченные подмножества
. Будем выбирать из этого множества различные упорядоченные подмножества  из k элементов.
из k элементов. элементов множества Х.
элементов множества Х. (размещения с повторениями).
(размещения с повторениями). и определяется равенством
и определяется равенством
 . Если цифры не повторяются, то
. Если цифры не повторяются, то  .
.




 В
В 




 = a
= a 








 - нулевой вектор, обозначается
- нулевой вектор, обозначается  . Длина вектора
. Длина вектора  обозначается |
обозначается |  ,
,  ,
,  - некомпланарные векторы, то любой вектор
- некомпланарные векторы, то любой вектор  можно представить в виде:
можно представить в виде:



