Свойства степеней
Пример.
3. Логарифмы и их свойства. Логари́фм числа Свойства логарифмов: 1° 2° 3° Логарифм единицы по любому положительному, отличному от 1, основанию равен нулю. Это возможно потому, что из любого действительного числа можно получить 1 только возведя его в нулевую степень. 4° Логарифм произведения равен сумме логарифмов сомножителей. 5° Логарифм частного (дроби) равен разности логарифмов сомножителей. 6° Логарифм степени равен произведению показателя степени на логарифм ее основания. 7° 8° 9°
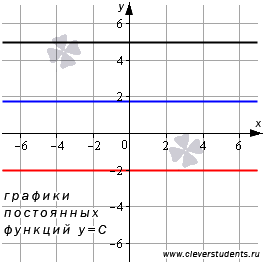
4. Понятие функции, их свойства и графики. Основными элементарными функциями являются: постоянная функция (константа), корень n-ой степени, степенная функция, показательная, логарифмическая функция, тригонометрические и обратные тригонометрические функции. Постоянная функция. Постоянная функция задается на множестве всех действительных чисел формулой Графиком постоянной функции является прямая, параллельная оси абсцисс и проходящая через точку с координатами (0,C). Для примера покажем графики постоянных функций y=5, y=-2 и
|

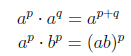



 по основанию определяется[2] как показатель степени, в которую надо возвести основание
по основанию определяется[2] как показатель степени, в которую надо возвести основание  , чтобы получить число
, чтобы получить число  , произносится: «логарифм
, произносится: «логарифм 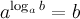 - основное логарифмическое тождество.
- основное логарифмическое тождество.

 - логарифм произведения.
- логарифм произведения. - логарифм частного.
- логарифм частного. - логарифм степени.
- логарифм степени.

 - переход к новому основанию.
- переход к новому основанию. , где C – некоторое действительное число. Постоянная функция ставит в соответствие каждому действительному значению независимой переменной x одно и то же значение зависимой переменной y – значение С. Постоянную функцию также называют константой.
, где C – некоторое действительное число. Постоянная функция ставит в соответствие каждому действительному значению независимой переменной x одно и то же значение зависимой переменной y – значение С. Постоянную функцию также называют константой. , которым на рисунке, приведенном ниже, отвечают черная, красная и синяя прямые соответственно.
, которым на рисунке, приведенном ниже, отвечают черная, красная и синяя прямые соответственно.