Контрольная работа №3. «Функции нескольких переменных»
Сон Л.Д., Русаков Г.М.
«Функции нескольких переменных» Задание I. Для данной функции найти производную по направлению данного вектора
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
Задание II. Заданы поверхность и кривая. Найти углы между ними в точках их пересечения.
1. Кривая:
2. Кривая:
3. Кривая:
4. Кривая:
5. Кривая: 6. Кривая:
7. Кривая:
8. Кривая:
9. Кривая:
10. Кривая:
Задание III. Для плоской фигуры с единичной плотностью, ограниченной данными кривыми, найти массу и положение центра тяжести.
1.
3.
5.
7.
9.
Задание IV. Для тела с единичной плотностью, ограниченного данными поверхностями, найти массу и момент инерции относительно оси oz.
1.
3.
5.
7.
9.
Задание V. Дано векторное поле
1. поле:
2. поле:
3. поле:
4. поле:
5. поле:
6. поле:
7. поле:
8. поле:
9. поле:
10. поле:
|

 в указанной точке
в указанной точке  .
.









 поверхность:
поверхность:  .
. поверхность:
поверхность:  .
. поверхность:
поверхность:  .
. поверхность:
поверхность:  .
. поверхность:
поверхность:  .
. поверхность:
поверхность:  .
. поверхность:
поверхность: 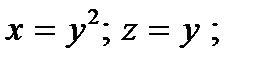 поверхность:
поверхность:  .
. поверхность:
поверхность:  .
. поверхность:
поверхность:  .
. 2.
2. 
 4.
4. 
 6.
6. 

 10.
10. 
 2.
2. 
 4.
4. 
 6.
6. 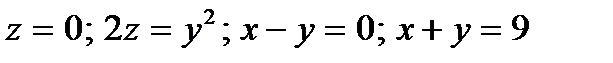
 8.
8. 
 10.
10. 
 и плоскость
и плоскость  , которая вместе с координатными плоскостями образует пирамиду. При этом
, которая вместе с координатными плоскостями образует пирамиду. При этом  - грань пирамиды, принадлежащая упомянутой плоскости, а λ; - контур, который ограничивает
- грань пирамиды, принадлежащая упомянутой плоскости, а λ; - контур, который ограничивает  ; плоскость:
; плоскость:  ;
; ; плоскость:
; плоскость:  ;
; ; плоскость:
; плоскость:  ;
; ; плоскость:
; плоскость:  ;
; ; плоскость:
; плоскость:  ;
;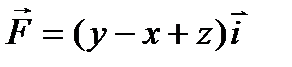 ; плоскость:
; плоскость:  ;
; ; плоскость:
; плоскость:  ;
; ; плоскость:
; плоскость: 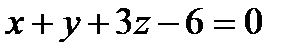 ;
; ; плоскость:
; плоскость:  ;
; ; плоскость:
; плоскость:  ;
;


