Энергия. Введенное понятие импульса, как некоторая мера механического движения, не во всех случаях пригодна для оценки изменения движения тела или его механического
Введенное понятие импульса, как некоторая мера механического движения, не во всех случаях пригодна для оценки изменения движения тела или его механического состояния. Существует другая мера движения тела, кроме импульса, особенно необходимая там, где происходит превращение механического движения тела в другие виды движения. Такой мерой движения, пригодной для всех случаев, является физическая величина, называемая энергией. Энергия - скалярная физическая величина, являющаяся общей мерой различных форм движения материи, рассматриваемых в физике. Энергия системы количественно характеризует последнюю в отношении возможных в ней превращений движения. Эти превращения происходят благодаря взаимодействию частей системы как друг с другом, так и с внешними телами. Для анализа качественно различных форм движения и соответствующих им взаимодействий в физике вводят различные виды энергии: механическую, внутреннюю, электромагнитную, ядерную и др. Энергия является важнейшей физической величиной, характеризующей способность тел или системы тел совершать работу и измеряется величиной работы, которую при определенных условиях может совершить система, т.е.
Одной из разновидностей механической энергии является энергия, обусловленная движением тел и зависящая от скорости движения. Эта энергия получила название кинетической и определяется по формуле:
Другой разновидностью механической энергии является потенциальная энергия ЕP, обусловленная взаимным расположением всех частей системы во внешнем поле потенциальных сил,
Единой формулы для вычисления потенциальной энергии нет, выражение для вычисления потенциальной энергии определяется видом взаимодействия. Работа консервативных (потенциальных) сил всегда равна убыли потенциальной энергии.
Величина Е, равная сумме кинетической и потенциальной энергий называется полной механической энергией тела.
Для замкнутой системы тел, в которой действуют только консервативные силы, полная механическая энергия системы остается неизменной ( Если в системе действуют неконсервативные силы, например, силы трения, то закон сохранения энергии в данной выше форме неприменим. Но его можно обобщить и на случай любых сил, если учесть переход энергии из механической в другой вид, например, во внутреннюю, электрическую и др. В природе и технике постоянно происходят превращения энергии из одних видов в другие. Все такие переходы происходят с соблюдением закона сохранения энергии. Таким образом, закон сохранения энергии подчеркивает количественную неизменность энергии изолированной системы во времени, в результате изменения формы движения, и выражает однородность времени. Это свойство времени проявляется в том, что законы движения замкнутой системы не зависят от выбора начала отсчета времени. Использование законов сохранения энергии и импульса позволяет решать многие задачи механики, не прибегая непосредственно к уравнениям движения. Удар а) классическая теория удара Интересные превращения кинетической энергии в потенциальную и обратно наблюдаются при ударе тел. Ударом называется кратковременное взаимодействие тел, при этом оба тела деформируются и возникают ударные силы значительной величины. Процесс соударения можно разделить на две фазы: 1. Сближение тел - возникновение деформаций. 2. Разлет - исчезновение деформаций (полное или частичное). Различают два предельных случая: абсолютно упругий и абсолютно неупругий удары. При абсолютно упругом ударе на первой фазе кинетическая энергия переходит полностью или частично в потенциальную энергию упругой деформации, на второй фазе тела снова приобретают первоначальную форму, отталкивая друг друга. В итоге потенциальная энергия упругой деформации опять переходит в кинетическую и тела разлетаются. При абсолютно упругом ударе механическая энергия тел не переходит в другие немеханические виды энергии. Рассмотрим абсолютно упругий удар двух шаров, центры которых движутся вдоль одной прямой. При этом движение вправо будет соответствовать положительной скорости, движение влево - отрицательной. При абсолютно упругом ударе не выделяется теплота, следовательно систему из двух взаимодействующих шаров можно считать замкнутой (консервативной). К такой системе можно применить закон сохранения импульса и энергии. Обозначим массы шаров m1 и m2, их скорости до удара
Рис. 1. Удар шаров: а) положение до удара; б) положение после удара Применяем к двум взаимодействующим шарам законы сохранения энергии и импульса:
Перенося слагаемые, содержащие m1 в одну, а m2 в другую сторону равенства, получим:
Деление равенства (1.10) на (1.11) дает:
Решая совместно уравнения (1.11) и (1.12), находим значения скоростей U1 и U2:
По этим формулам определяются скорости шаров после удара. Следует помнить, что в формулах (1.13) скорости U1 и U2 могут иметь как одинаковые, так и противоположные знаки, в зависимости от направления векторов 1, Преобразуем равенство (1.12)
В левой части равенства (1.14) Вывод: относительная скорость шаров после удара остается по абсолютной величине равной относительной скорости шаров до удара, но меняет знак на противоположный. 2. Положим Вывод: при упругом центральном ударе двух шаров одинаковой массы, шары обмениваются скоростями. 3. Пусть Вывод: при ударе шара о массивную стенку его скорость меняется на противоположную, скорость же стенки практически не изменяется. Абсолютно упругий удар является идеальным случаем. В реальных случаях в зависимости от того, из какого вещества изготовлены шары, большая или меньшая часть механической энергии переходит в тепло. Абсолютно неупругий удар характеризуется тем, что потенциальная энергия упругой деформации не возникает, кинетическая энергия тел полностью или частично превращается во внутреннюю энергию, после удара сталкивающиеся тела либо покоятся, либо движутся с одинаковой скоростью. При таком ударе шары деформируются, скорости их выравниваются, суммарная кинетическая энергия шаров после удара уменьшается по сравнению с первоначальной (до удара), так как часть ее перейдет в другие формы энергии - тепловую, энергию пластических деформаций и т.д. Для этого случая закон сохранения энергии запишется в виде:
Система из двух шаров в этом случае будет являться диссипативной, так как часть механической энергии теряется, рассеивается и по формуле (1.15) можно определить потерю механической энергии Q, которую называют энергией диссипации. Скорость же шаров после удара можно найти, воспользовавшись законом сохранения импульса:
откуда
При абсолютно неупругом ударе относительная скорость шаров после удара равна нулю:
где Из формулы (1,17) определяется величина коэффициента восстановления
|

 . (1.5)
. (1.5)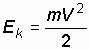 . (1.6)
. (1.6) .
. (1.7)
(1.7)
 ), в этом заключается закон сохранения механической энергии.
), в этом заключается закон сохранения механической энергии. и
и  , а после удара
, а после удара  и
и  (рис. 1).
(рис. 1).
 (1.8)
(1.8) (1.9)
(1.9) (1.10)
(1.10) (1.11)
(1.11) . (1.12)
. (1.12)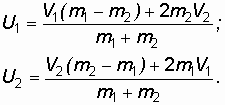 (1.13)
(1.13) и
и 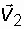 . Проведем анализ полученных результатов по формулам (1.12) и (1.13).
. Проведем анализ полученных результатов по формулам (1.12) и (1.13). или
или  . (1.14)
. (1.14) - есть относительная скорость шаров до удара, в правой
- есть относительная скорость шаров до удара, в правой  - относительная скорость шаров после удара.
- относительная скорость шаров после удара. , тогда из первого равенства (1.13) следует, что
, тогда из первого равенства (1.13) следует, что  и из второго равенства (1.13) следует
и из второго равенства (1.13) следует  .
. и
и  , тогда из равенства (1.13) получим:
, тогда из равенства (1.13) получим: 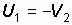 , а
, а  .
. . (1,15)
. (1,15) ,
, . (1.16)
. (1.16)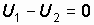 , так как
, так как  . При абсолютно упругом ударе она, как известно, равна:
. При абсолютно упругом ударе она, как известно, равна: 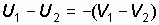 . При частично неупругом ударе относительная скорость после удара будет составлять некоторую долю относительной скорости шаров до удара:
. При частично неупругом ударе относительная скорость после удара будет составлять некоторую долю относительной скорости шаров до удара: , (1.17)
, (1.17) - коэффициент восстановления относительной скорости шаров при ударе, характеризующий степень упругости взаимодействующих тел и может принимать значения
- коэффициент восстановления относительной скорости шаров при ударе, характеризующий степень упругости взаимодействующих тел и может принимать значения  .
.



