Принципы симметрии

Симметрия является той идеей, посредством которой человек на протяжении веков пытался по­стичь и создать порядок, красоту и совершенство.

Г. Вейль

Термин "симметрия";в переводе с греческого означает сораз­мерность, пропорциональность, одинаковость в расположении частей. Античные философы считали симметрию, порядок и опре­деленность сущностью прекрасного. "Краткий Оксфордский сло­варь" определяет симметрию как красоту, обусловленную про­порциональностью частей тела или любого целого, равновесием, подобием, гармонией, согласованностью. Однако оно не охватыва­ет всей глубины и широты данного понятия.

С симметрией мы встречаемся везде - в природе, технике, нау­ке, искусстве. Она существует не только в макромире, но и прису­ща микро- и мегамиру. Симметрия, понимаемая в самом широком смысле, противостоит хаосу, беспорядку, она наблюдается везде, где есть хоть какая-то упорядоченность. В этом смысле симмет­ричны не только объекты природы (снежинки, листья, рыбы, на­секомые, человеческое тело и т.д.), но и такие упорядоченные яв­ления, как регулярная смена дня и ночи, времен года, круговорот воды и других веществ в природе и др. Идею симметрии можно выразить и такими словами, как уравновешенность, гармония, совершенство.

Для человека симметрия обладает притягательной силой. Нам нравится смотреть на проявление симметрии в природе: симмет­ричные кристаллы, снежинки, цветы, которые почти симметрич­ны. Архитекторы, художники, поэты и музыканты с древнейших времен знали законы симметрии. Строго симметрично строятся геометрические орнаменты; в классической архитектуре господ­ствуют прямые линии, углы, круги, равенство колонн, окон, арок и сводов. Конечно, симметрия в искусстве не буквальная. Зако­ны симметрии художественного произведения подразумевают не однообразие форм, а глубокую согласованность элементов.

Понятие симметрии проходит через всю многовековую историю человеческого творчества. Законы природы, управляющие беско­нечным многообразием картины явлений, также подчиняются сим-

метрии. Симметрию можно обнаружить практически всюду, если знать, где и как ее искать. Все разнообразие окружающего нас мира подчинено удивительным проявлениям симметрии. Об этом очень удачно написал Дж.Ньюмен: "Симметрия устанавливает за­бавное и удивительное сродство между предметами, явлениями и творениями, внешне, казалось бы, ничем не связанными: зем­ным магнетизмом, женской вуалью, поляризованным светом, есте­ственным отбором, теорией групп, инвариантами и преобразовани­ями, рабочими привычками пчел в улье, строением пространства, рисунками ваз, квантовой механикой, лепестками цветов, интер­ференционной картиной рентгеновских лучей, делением клеток, равновесными конфигурациями кристаллов, снежинками, музы­кой, теорией относительности..." (Цит. по кн.: Тарасов Л.В. Этот удивительно симметричный мир, 1982.)

Строгое математическое представление о симметрии сформиро­валось сравнительно недавно - в XIX в. Современный подход к симметрии предполагает неизменность объекта по отношению к каким-нибудь выполняемым над ним операциям или преобразо­ваниям. Современное определение симметрии формулируется так: симметричным называется объект (предмет), который можно как-то изменять, получая в результате объект, совпадающий с первоначальным. Согласно определению, прежде всего должен существовать объект - носитель симметрии. Для разных про­явлений симметрии он, конечно, разный. Это материальные пред­меты или свойства. У объектов должны существовать некоторые признаки - свойства, процессы, отношения, явления, которые не изменяются при операциях симметрии. Также должны про­исходить изменения этих объектов, но не какие угодно, а толь­ко такие, которые переводят его в тождественный самому себе. И, наконец, должно существовать свойство объекта, которое при этом не изменяется, т.е. остается инвариантным.

Подчеркнем, что инвариантность существует не сама по себе, не вообще, а лишь по отношению к определенным преобразовани­ям, а изменения (преобразования) представляют интерес постоль­ку, поскольку что-то при этом сохраняется. Другими словами, без изменения не имеет смысла рассматривать сохранение, равно как без сохранения исчезает интерес к изменениям. Таким образом, симметрия выражает сохранение чего-то при каких-то изме­нениях или сохранение чего-то несмотря на изменение. Сим-

метрия предполагает неизменность не только самого объекта, но и каких-либо его свойств по отношению к преобразованиям, вы­полненным над объектом.

Неизменность тех или иных объектов может наблюдаться по отношению к разнообразным операциям - к поворотам, перено­сам, взаимной замене частей, отражениям и т.д. В связи с этим выделяют разные типы симметрии.

ПОВОРОТНАЯ СИММЕТРИЯ. Говорят, что объект обладает поворотной симметрией, если он совмещается сам с собой при повороте на угол 2тг /п, где п может равняться 2, 3, 4 и т.д. до бесконечности. Ось симметрии называется ось осью п-го порядка.

ПЕРЕНОСНАЯ (ТРАНСЛЯЦИОННАЯ) СИММЕТРИЯ. О та­кой симметрии говорят тогда, когда при переносе фигуры вдоль прямой на какое-то расстояние а либо расстояние, кратное этой величине, она совмещается сама с собой. Прямая, вдоль которой производится перенос, называется осью переноса, а расстояние а - элементарным переносом или периодом. С данным типом симметрии связано понятие периодических структур или решеток, которые могут быть и плоскими, и пространственными.

ЗЕРКАЛЬНАЯ СИММЕТРИЯ. Зеркально симметричным счи­тается объект, состоящий из двух половин, которые являются зер­кальными двойниками по отношению друг к другу. Трехмерный объект преобразуется сам в себя при отражении в зеркальной плоскости, которую называют плоскостью симметрии.

СИММЕТРИИ ПОДОБИЯ представляют собой своеобразные аналоги предыдущих симметрии с той лишь разницей, что они связаны с одновременным уменьшением или увеличением подоб­ных частей фигуры и расстояний между ними. Простейшим при­мером такой симметрии являются матрешки.

Иногда фигуры могут обладать разными типами симметрии. Например, поворотной и зеркальной симметрией обладают неко­торые буквы: Ж, Н, Ф, О, X.

Выше перечислены так называемые геометрические симметрии. Существует много других видов симметрии, имеющих абстракт­ный характер. Например, ПЕРЕСТАНОВОЧНАЯ СИММЕТРИЯ, которая состоит в том, что если тождественные частицы поменять местами, то никаких изменений не происходит; НАСЛЕДСТВЕН­НОСТЬ - это тоже определенная симметрия.

КАЛИБРОВОЧНЫЕ СИММЕТРИИ связаны с изменением масштаба. Например, известно, что при подъеме тела на неко­торую высоту затраченная энергия зависит лишь от разности на­чальной и конечной высоты, но не зависит от абсолютной высоты. Говорят, что существует симметрия начала отсчета высот, ее и относят к классу калибровочных симметрии. Все фундаменталь­ные взаимодействия имеют калибровочную природу и описыва­ются калибровочными симметриями. Этот факт отражает един­ство всех фундаментальных взаимодействий. Калибровочная ин­вариантность позволяет ответить на вопрос: "Почему и зачем в природе существует такого рода взаимодействия?" Это обусловле­но тем, что требование калибровочной инвариантности порождает конкретный вид взаимодействия. Поэтому форму взаимодействия уже не постулируют, а она выводится как результат калибровоч­ной инвариантности.

На этом принципе строится единая теория всех физических взаимодействий. Интересно заметить, что этот принцип выходит далеко за рамки физики и может стать мощным регулятивным принципом при решении проблем социального и экономическо­го характера. Думается, такие принципы, как социальная спра­ведливость, равенство, устойчивый уровень жизни населения и другие, могут быть поставлены в соответствие с некоторой сим­метрией.

В неживой природе симметрия прежде всего возникает в таком явлении природы, как кристаллы, из которых состоят практиче­ски все твердые тела. Именно она и определяет их свойства. Са­мый очевидный пример красоты и совершенства кристаллов - это известная всем снежинка. Все снежинки, несмотря на разнообра­зие их форм, обладают зеркальной и поворотной симметрией 6-го порядка. Доказано, что все кристаллы могут обладать поворотной симметрией 2, 3, 4 и 6-го порядков. Симметрия кристалла свя­зана с наличием кристаллической решетки - пространственной решетки из атомов. Отсюда видно, что симметрия ограничивает возможности вариантов структур.

Физические законы и явления также подчиняются законам сим­метрии. Р. Фейнман писал, что "все многообразие законов физи­ки пронизано несколькими общими принципами, которые так или иначе содержатся в каждом законе. Примерами таких принципов могут служить некоторые свойства симметрии" (Фейнман, 1987).

Существует несколько симметрии физических законов:

1. Физические законы неизменны, инвариантны по отношению к
переносам в пространстве, что обусловлено однородностью про­
странства. Это значит, что при переносе какого-либо устройства
из одной точки пространства в другую его свойства, особенности
функционирования и результаты опытов не изменятся.

2. Физические законы инвариантны по отношению к поворо­
там в пространстве. Это называют изотропностью простран­
ства. Например, на север ли, на восток ли повернута установка,
результаты опыта будут одни и те же.

 

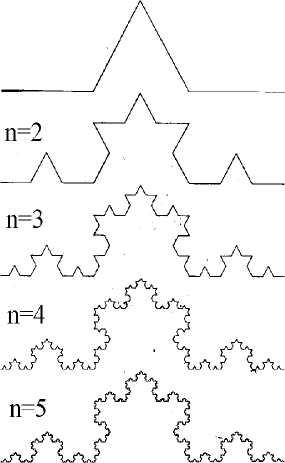
3. Симметрия физических законов определяется и однородно­
стью времени, т.е. они инвариантны по отношению к ереносам во времени. Таким образом, однородность пространства и времени являются свойствами симметрии.

4. Принцип относительности законов природы - это тоже
симметрия по отношению к переходу из одной инерциальной си­
стемы отсчета в другую. Эта симметрия устанавливает равнознач­
ность всех инерциальных систем отсчета.

5. Никакие физические явления не изменяются при переста­
новке двух идеально одинаковых частиц (например, электронов
или протонов) - перестановочная симметрия.

6. Еще один вид симметрии физических законов - инвариант­
ность по отношению к зеркальному отражению. Это значит,
что две физические установки, одна из которых построена как зер­
кальное отображение другой, будут функционировать одинаково.
Отметим, что эта симметрия при определенных взаимодействиях
нарушается.

Свойства симметрии относятся к числу самых фундаменталь­ных свойств физических систем. Однако не все законы природы инвариантны к любым преобразованиям. Например, геометриче­ский принцип подобия не применим к физическим законам. Еще Г. Галилей догадался, что законы природы несимметричны отно­сительно изменения масштаба. Р. Фейнман приводит пример с мо­делью собора, который сложен из спичек. Если ее увеличить до натуральных размеров, то строение разрушится под собственной тяжестью. С точки зрения современной физики отсутствие сим­метрии физических законов относительно преобразования подобия объясняется тем, что порядок размеров атомов имеет абсолютное, одинаковое для всей Вселенной значение. Законы классической

физики перестают работать в микромире, вместо них приходят законы квантовой механики. Это уже проявление асимметрии, т.е. несимметрии.

Между симметрией и законами сохранения существует глубо­кая связь. В начале XX в. Э. Нётер сформулировала теорему, согласно которой если свойства системы не изменяются от какого-либо преобразования над ней, то этому соответствует некоторый закон сохранения — теорема Нётер. Поскольку независимость свойств от преобразования означает наличие в системе симметрии относительно данного преобразования, постольку теорема Нётер может быть сформулирована как утверждение о том, что наличие в системе симметрии обуславливает существование для нее сохра­няющейся физической величины. Так, например, закон сохранения импульса есть следствие однородности пространства, а закон со­хранения энергии - следствие однородности времени. Законы со­хранения, действуя в самых различных областях и в различных конкретных ситуациях, выражают то общее для всех ситуаций, что в конечном счете связано с соответствующими принципами симметрии. Таким образом, симметрия связана с сохранением и выделяет в нашем изменчивом мире различные инварианты - некие своеобразные "опорные точки". Можно сказать, что сим­метрия вносит порядок в наш мир. В окружающем нас мире "все течет, все изменяется," он наполнен взаимодействиями и превра­щениями, всюду присутствует случайность и неопределенность. Но при этом законы мира обнаруживают симметрию: энергия сохраняется, за летом следует зима и т.п. Симметрия выделя­ет общее как в объектах, так и в явлениях, подчеркивая, что несмотря на то, чтомир многообразен, но в то же время он и един, так как в разнообразных явлениях природы присутствуют чер­ты общности.

В мире живой природы также проявляются все основные виды геометрических симметрии. Специфика строения растений и жи­вотных определяется особенностями среды обитания, к которой они приспосабливаются, особенностями их образа жизни. У любо­го дерева есть основание и вершина, "верх" и "низ", выполняющие разные функции. Значимость различия верхней и нижней частей, а также направление силы тяжести определяют вертикальную ориентацию поворотной оси "древесного конуса" и плоскостей симметрии. Для листьев характерна зеркальная симметрия. Эта

же симметрия встречается и у цветов, однако у них зеркальная симметрия чаще выступает в сочетании с поворотной симметрией. Нередки случаи и переносной симметрии (веточки акации, ряби­ны). Интересно, что в цветочном мире наиболее распростране­на поворотная симметрия 5-го порядка, которая принципиаль­но невозможна в периодических структурах неживой природы. Этот факт академик Н. Белов объясняет тем, что ось 5-го поряд­ка - своеобразный инструмент борьбы за существование, "стра­ховка против окаменения, кристаллизации, первым шагом которой была бы их поимка решеткой" (цит. по кн.: [37]). Действительно, живой организм не имеет кристаллического строения в том смыс­ле, что даже отдельные его органы не обладают пространственной решеткой. Однако упорядоченные структуры в ней представлены очень широко.

В мире рыб, насекомых, птиц, млекопитающих характерна би­латеральная симметрия (билатеральный в переводе с латинского - "дважды боковой") - так в биологии называют зеркальную сим­метрию. Это обусловлено тем, что в отличие от растений, которые не меняют места жительства, для животных актуально перемеще­ние в пространстве: у них нет симметрии относительно того на­правления, в котором они передвигаются, т.е. задняя и передняя части животного асимметричны. Плоскость симметрии у живот­ных, кроме вектора направления движения, определяется, как и у растений, направлением силы тяжести. Эта плоскость делит жи­вотное на две половины - правую и левую. Это же относится и к человеку.

Симметрия подобия проявляется в природе во всем, что рас­тет. Ствол дерева имеет вытянутую коническую форму. Ветви обычно располагаются вокруг ствола по линии, похожей на винто­вую, но она постепенно суживается к вершине. Это пример сим­метрии подобия с винтовой осью симметрии. Всякий живой организм повторяет себя в подобном. Природа обнаруживает по­добие как свою глобальную генетическую программу. Подобие правит живой природой в целом. Геометрическое подобие счи­тается общим принципом пространственной организации живых структур. Лист березы подобен другому листу березы и т.п.

Есть еще одна замечательная симметрия - самоподобие или масштабная инвариантность (скейлинг),которая имеет самое прямое отношение к природе. При построении моделей, описыва­ющих окружающий нас мир, мы привыкли использовать такие из

вестные геометрические понятия, как линия, круг, сфера, квадрат, куб и другие. Но на самом деле мир устроен по более сложным законам. Оказалось, что не всегда можно ограничиться такими простыми понятиями, т.е. мир не всегда можно изучать, используя только "линейку и циркуль". Геометрия Евклида не способна опи­сать форму ни облаков, ни гор, ни деревьев, ни берега моря. Дело в том, что облака - это не сферы, горы - не конусы и т.д. При­рода демонстрирует нам совершенно другой уровень сложности, чем мы привыкли считать. В природных структурах, как правило, число различных масштабов бесконечно.

Математики разработали математические понятия, выходящие за рамки традиционной геометрии, идеи которой, как теперь на­чинают понимать, позволяют все глубже постигать сущность при­роды. Одним из таких ярких примеров можно назвать фракталь­ную геометрию, центральным понятием которой является поня­тие "фрактала". На русский язык это слово переводится как "из­ломанный объект с дробной размерностью";.

Существует множество различных определений фрактала. Пре­жде всего, математическое понятие фрактала выделяет объекты, обладающие структурами различных масштабов, отражая иерар­хический принцип организации. Фракталы обладают свойством самоподобия: их вид существенно не изменяется при рассмот­рении через микроскоп с различным увеличением, т.е. фрактал выглядит практически одинаково, в каком бы масштабе его не на­блюдали. Другими словами, фрактал состоит из однотипных эле­ментов разных масштабов и, по сути, представляет собой повторя­ющийся при изменении масштабов узор. Малый фрагмент такого объекта подобен другому, более крупному фрагменту, или даже структуре в целом. Поэтому и говорят, что фрактал есть струк­тура, состоящая из частей, которые подобны целому. Фрак­талы в какой-то степени отражают принцип восточной мудрости: "одно во всем, и все в одном".

Главная особенность фракталов состоит в том, что они име­ют дробную размерность, являющуюся следствием масштабной инвариантности. С математической точки зрения геометрические объекты, в том числе и фракталы, можно рассматривать как мно­жество точек, вложенных в пространство. Например, множество точек, образующих линию в евклидовом пространстве, имеют раз­мерность D = 1, а множество точек, образующих поверхность в трехмерном пространстве, имеют размерность D = 2. Шар имеет размерность D = 3. Их характерная особенность состоит в том, что длина линии, площадь поверхности или объем пропорциональ­ны, соответственно, линейному масштабу в первой, во второй или третьей степени, т.е. их размерность совпадает с размерностью пространства, в которое они вложены. Однако существуют объ­екты, для которых это не так. К таким объектам, в частности, относятся фракталы, размерность которых выражается дробным числом 1 < Dj < 3, где Df - фрактальная размерность. На рис. 2.1 показан один из таких типичных примеров, демонстри­рующих, что кривая может иметь размерность Df > 1, так называемая кривая Кох.

Она строится следующим образом. Исходный отрезок единич­ной длины делится на три равные части. Затем выполняются по­строения, показанные на рис. 2.1. В результате в первом поко­лении (п = 1) получаем ломаную кривую, состоящую из четы­рех звеньев длиной по 1/3. Длина всей кривой в этом поколении составляет £(1/3) = 4/3. Следующее поколение (п = 2) получа­ется путем той же самой операции над каждым прямолинейным звеном первого поколения. Здесь получается кривая, состоящая из N = 4² = 16 звеньев, каждое длиной 5 = З"² = 1/9. Вся длина равна L(l/9) = (4/3)² = 16/9. И так далее. На n-м ша­ге длина прямолинейного звена 6 = 3~^п. Число поколений можно представить в виде п = — 1п^/1пЗ, а длина всей ломаной L(5) = (4/3)" = ex_Pln£[ln4-ln3]/ln3 = 6¹~^Df, D_f = Ш/Ш = 1,2628. Число сегментов N(6) = 4^п = 4~^1пй/^1п3 и может быть записано как N(5) = 5~^Df, где Df - фрактальная размерность кривой Кох. Таким образом, кривая Кох есть фрактал с фрактальной размер­ностью Df = In 4/3. Подобным образом можно построить много разновидностей и других фракталов. Можно построить и такие объекты, для которых необходимо вводить не одну, а несколько размерностей. Иногда такие объекты называют математически­ми фракталами, которые, в отличие от природных или физиче­ских фракталов, обладают идеальным самоподобием. Для физи­ческих фракталов (реально существующие объекты) самоподобие или масштабная инвариантность выполняется приближенно (или, как говорят, в среднем).

Примером фрактального объекта, часто встречающегося в при­роде, является береговая линия. На рис. 2.2 показана южная

11=1

 

 

Рис. 2.1. Построение триадной кри­вой Кох

Рис. 2.2. Побережье южной части Норвегии

часть побережья Норвегии, которое имеет вид сильно изрезан­ной линии. Можно показать, что измерить длину такой линии, используя обычные способы евклидовой геометрии, невозможно. Но для этой цели хорошо подходит фрактальная геометрия. Ока­залось, что длина береговой линии хорошо описывается формулой L(5) = a8^l~^Df, где 5 - используемый для измерения масштаб (на­пример, некоторый раствор циркуля), а - число единиц масштаба. Для побережья Норвегии это Dj ~ 1,52, для береговой линии Великобретании - Dj ~ 1,3. В природе фрактальные структуры встречаются часто: очертания облаков, дым, деревья, береговая линия и русла рек, трещины в материалах, бронхи легких, пори­стые губки, ветвящиеся подобно лишайникам структуры, поверх­ности порошков, артерии и реснички, покрывающие стенки ки­шечника, и многие другие, которые не имеют, на первый взгляд, закономерностей в своем строении. Но отсутствие порядка в них иллюзорно. Внешне они выглядят как изрезанные, "лохматые" или "дырявые" объекты, представляя собой нечто промежуточное меж­ду точками, линиями, поверхностями и телами.

Введение понятия фрактала и фрактальной геометрии позво­ляет выделить ранее скрытые закономерности в строении и свой­ствах природных объектов, имеющих неупорядоченную структуру, классифицировать и исследовать их свойства. Когда мы смотрим на фрактальный объект, то нам он представляется неупорядочен

ным. При увеличении или уменьшении масштаба мы опять увидим то же самое. Это и есть проявление свойства симметрии - мас­штабной инвариантности, или скейлинга. Именно оно и обу­славливает их необычные свойства. Благодаря самоподобию фрак­талы обладают удивительно притягивающей красотой, которой нет в других объектах. Они могут описывать многие процессы, ко­торые до сих пор не удавалось описать, благодаря своей дробной размерности и самоподобию. Даже считается, что фрактальный мир гораздо ближе к реальному, так как свойства фракталов де­монстрируют многие природные объекты. Видимо, не зря говорят, что природа любит фракталы.

Столь удивительное сходство реального мира и фрактального обусловлено, прежде всего, тем, что свойства физического мира изменяются медленно с изменением масштабов. У песка на берегу много свойств, общих со свойствами гальки. Маленький ручеек во многом похож на большую реку. Такая неизменность относи­тельно масштаба - характерная черта фракталов. В живой природе внешний вид и внутреннее строение заданы в генотипе алгоритми­чески. Ветка дерева похожа на само дерево, поскольку построена по тому же алгоритму. Это относится и к кровеносной системе животных, человека, и к сложным листьям некоторых растений.

Различные фрактальные множества можно получать и с по­мощью простых (элементарных) преобразований, например, типа х_п+1 = х'²_п + с, где с - некоторое комплексное число, п = 1,2,3.... Множество чисел, полученных по этой формуле, при определен­ных значениях с также обладают свойствами фракталов. Отоб­ражая их на плоскости или в трехмерном пространстве, получа­ют удивительно красивые изображения (см., например, рис. 2.3 и рис. 2.4).

Интересно отметить, что фрактальная математика может быть использована для анализа изменений цен и заработной платы, ста­тистики ошибок на телефонных станциях, частот слов в печатных текстах и т.д.

Подчеркнем, что симметрия в живой природе никогда не бывает абсолютной, всегда присутствует какая-то доля несимметрии. Хо­тя с симметрией мы встречаемся практически всюду, но при этом замечаем часто не ее, а ее нарушение. Асимметрия - другая сто­рона симметрии. Асимметрия - это несимметрия, т.е. отсутствие (нарушение) симметрии.

 

 

Рис. 2.3. Характерное изображение фракталь­ного множества Жюлиа

Рис. 2.4. "Глаз морского конька"

Симметрия и асимметрия - две полярные противоположности объективного мира. На разных уровнях развития материи присут­ствует то симметрия - относительный порядок, то асимметрия -тенденции нарушения покоя, движения, развития.

Асимметрия присутствует уже на уровне элементарных частиц и проявляется в абсолютном преобладании в нашей Вселенной частиц над античастицами. Известный физик Ф. Дайсон писал: "Открытия последних десятилетий в области физики элементар­ных частиц заставляют нас обратить особое внимание на кон­цепцию нарушения симметрии. Развитие Вселенной с момента ее зарождения выглядит как непрерывная последовательность нару­шений симметрии. В момент своего возникновения при грандиоз­ном взрыве Вселенная была симметрична и однородна. По мере остывания в ней нарушается одна симметрия за другой, что со­здает возможности для существования все большего и большего разнообразия структур. Феномен жизни естественно вписывается в эту картину. Жизнь - это тоже нарушение симметрии" (цит. по ст.: И. Акопян // Знание - сила. 1989).

Молекулярная асимметрия открыта Л. Пастером, который пер­вым выделил "правые" и "левые" молекулы винной кислоты: пра­вые молекулы похожи на правый винт, а левые - на левый. Та­кие молекулы химики называют стереоизомерами. Молекулы-стереоизомеры имеют одинаковый атомный состав, одинаковые размеры, одинаковую структуру - в то же время они различи­мы, поскольку являются зеркально асимметричными, т.е. объект оказывается нетождественным со своим зеркальным двойником.

Поэтому здесь понятия "правый-левый" - условны. В настоящее время хорошо известно, что молекулы органических веществ, со­ставляющие основу живой материи, имеют асимметричный характер, т.е. в состав живого вещества они входят только либо как правые, либо как левые молекулы. Таким образом, каждое вещество может входить в состав живой материи только в том случае, если оно обладает вполне определенным типом симмет­рии. Например, молекулы всех аминокислот в любом живом орга­низме могут быть только левыми, сахара - только правыми. Это свойство живого вещества и его продуктов жизнедеятельности на­зывают дисимметрией. Оно имеет совершенно фундаментальный характер. Хотя правые и левые молекулы неразличимы по хими­ческим свойствам, живая материя их не только различает, но и делает выбор. Она отбраковывает и не использует молекулы, не обладающие нужной ей структурой. Как это происходит, пока не ясно. Молекулы противоположной симметрии для нее яд. Если бы живое существо оказалось в условиях, когда вся пища была бы составлена из молекул противоположной симметрии, не отвечаю­щей дисимметрии этого организма, то оно погибло бы от голода. В неживом веществе правых и левых молекул поровну.

Дисимметрия - единственное свойство, благодаря которому мы можем отличить вещество биогенного происхождения от неживого вещества. Мы не можем ответить на вопрос, что такое жизнь, но имеем способ отличить живое от неживого. Таким об­разом, асимметрию можно рассматривать как разграничительную линию между живой и неживой природой. Для неживой материи характерно преобладание симметрии, при переходе от неживой к живой материи уже на микроуровне преобладает асимметрия. В живой природе асимметрию можно увидеть всюду. Очень удачно это подметил в романе "Жизнь и судьба" В. Гроссман: "В боль­шом миллионе русских деревенских изб нет и не может быть двух неразличимо схожих. Все живое неповторимо. Немыслимо тожде­ство двух людей, двух кустарников шиповника... Жизнь глохнет там, где насилие стремится стереть ее своеобразие и особенности".

Симметрия и асимметрия составляют единство, они взаимосвя­заны друг с другом, как две стороны одной медали. Нельзя пред­ставить полностью симметричный мир, так же как и невозможно помыслить о мире, вообще лишенном симметрии. Симметрия ле­жит в основе вещей и явлений, выражая нечто общее, свойствен

ное разным объектам, тогда как асимметрия связана с индивиду­альным воплощением этого общего в конкретном объекте.

На принципе симметрии основан метод аналогий, предполага­ющий отыскание общих свойств в различных объектах. На осно­ве аналогий создаются физические модели различных объектов и явлений. Аналогии между процессами позволяют описывать их общими уравнениями. Принципы симметрии лежат в основе тео­рии относительности, квантовой механики, физики твердого тела, атомной и ядерной физики, физики элементарных частиц. Разра­ботан метод решения задач из соображений симметрии.

Принципы симметрии выражают наиболее общие свойства при­роды, они имеют более общий характер, чем законы движения. Поэтому проверка принципов симметрии всегда интересовала фи­зиков, а поиск новых симметрии составляет одну из задач физики вообще. Поиски новых свойств симметрии — это вместе с тем по­иски и новых законов сохранения. Наши представления о симмет­рии устанавливаются путем обобщения опытных данных. Неко­торые симметрии оказываются только приближенными. С другой стороны, обобщая опыт, мы открываем новые законы сохранения и, следовательно, новые принципы симметрии.

Существует точка зрения, согласно которой в нашем познании о мире есть три ступени: уровень явлений или событий, зако­нов природы и принципов симметрии, поднимаясь на которые, мы глубже и дальше познаем природу, лучше ее понимаем. Уро­вень явлений самый элементарный. Это все, что происходит в ми­ре: движение тел, столкновения частиц, поглощение и излучение света и много других явлений. С первого взгляда кажется, что между ними нет ничего общего. Однако при более внимательном рассмотрении мы обнаруживаем, что между явлениями имеют­ся определенные взаимосвязи, которые и называют законами. В принципе, если бы мы располагали полной информацией обо всех явлениях и событиях в мире, то нам законы не были бы нужны. С другой стороны, если бы мы знали все законы или один всеобъем­лющий закон природы, то свойства инвариантности этих законов не давали бы ничего нового. Но, к сожалению, нам не известно даже большинство законов природы. Поэтому познание свойств симметрии, как писал Е. Вигнер, "состоит в наделении структу­рой законов природы или установлении между ними внутренней связи, так же как законы устанавливают структуру или взаимосвязь в мире явлений" (Вигнер, 1971). Поэтому говорят, что если законы управляют явлениями, то принципы симметрии - это законы физических законов. Таким образом, можно сказать, что симметрия характеризует собой эпоху синтеза, когда разроз­ненные знания сливаются в единую, целостную картину.

Выявление различных симметрии в природе, а иногда и посту­лирование их, стало одним из методов теоретического исследо­вания микро-, макро- и мегамира. Законы природы позволяют предсказывать явления, а принципы симметрии - открывать законы природы. Например, уравнения Максвелла в электродина­мике получены на основании симметрии между электрическими и магнитными явлениями. Д. Максвелл исходил из убеждения, что взаимодействия электрического и магнитного полей должны быть симметричными, и поэтому ввел в свои уравнения дополнитель­ное слагаемое, учитывающее это обстоятельство. Уверенность в симметрии законов природы привела его в выводу о существо­вании электромагнитных волн. Также можно сказать, что идея А. Эйнштейна, приведшая его к созданию теории относительно­сти, опиралась на уверенность в глубокой симметрии природы, которая должна одновременно охватывать механические, электро­магнитные и все другие явления.

О. Мороз в книге "В поисках гармонии" писал, что физики го­няются за симметрией подобно тому, как путники преследуют в пустыне ускользающий мираж. Вот возникла на горизонте пре­красная манящая картина, но как только вы попытаетесь к ней приблизиться, она исчезает, оставляя чувство горечи.