Молекулярная физика
№1. Автомобильные номера состоят из трех букв и четырёх цифр. Найти число таких номеров, если используется 32 буквы алфавита.
№2. Сколькими способами можно составить трехцветный полосатый флаг, если имеется материя 5 цветов? №3. В ящике имеется 15 деталей, среди которых 5 бракованных. Сборщик наудачу берёт 3 детали. Сколько будет случаев, когда среди извлеченных трёх деталей будут: а) все стандартные; б) две стандартные; в) все бракованные? №4. Сколько машинных слов можно составить из букв слова ВОДОРОД?
---------------------------------------------------------------------------------------------------------------- Комбинаторика. Стр.3 Контрольная работа по физике № 2 для студентов-заочников инженерно-технических специальностей Вариант 7 Электродинамика В вершинах правильного треугольника со стороной см расположены два положительных и один отрицательный заряды, равные по модулю: нКл. Определить напряженность и потенциал поля в центре треугольника.
Результирующая напряжённость Угол между векторами напряженностей равен
Таким образом, Потенциал поля системы точечных зарядов также подчиняется принципу суперпозиции, и для системы трёх положительных зарядов равен:
Ответ: Поле образовано бесконечной равномерно заряженной плоскостью с поверхностной плотностью заряда Кл/м2. Определить разность потенциалов двух точек поля, отстоящих от плоскости на расстоянии см и см по силовой линии. Решение: Так как образованное поле однородно, то связь между напряженностью и потенциалом будет следующая: Тогда, учтя что напряжённость поля, создаваемого бесконечной равномерно заряженной плоскостью равно
Ответ: Электрон перемещается от одной пластины плоского конденсатора до другой. Разность потенциалов между пластинами В, расстояние между ними мм. Определите: а) скорость, с которой электрон достигнет другой пластины (); б) время его движения; в) поверхностную плотность заряда на пластинах. Решение: В поле плоского конденсатора на электрон действует кулоновская сила: а) Для того, чтобы сообщить электрону кинетическую энергию Поскольку б) В результате действия постоянной силы электрон получает ускорение Если электрон прошёл расстояние в) Напряжённость поля плоского конденсатора: Окончательно поверхностная плотность заряда на пластинах будет равна:
Ответ: а) 37. Электрическая цепь состоит из двух гальванических элементов, трех сопротивлений и гальванометра (рис. 27):
1. Обозначаем на схеме контуры, узлы и направление токов (обозначим контур слева направо: 2. Устанавливаем число ветвей 3. Для составления уравнений по первому закону Кирхгофа: для узла В: 4. Устанавливаем число уравнений, необходимых для решения задач по второму закону Кирхгофа. Это число уравнений равно Выбираем контуры 5. Устанавливаем обход по контуру Составляем уравнение для второго контура Подставив в полученные равенства значения сопротивлений и ЭДС, получим систему уравнений (учтём, что по условию задачи
Из третьего уравнения выразим
Ответ: По кольцевому проводнику радиусом см течет ток А. Параллельно плоскости кольцевого проводника на расстоянии см над его центром проходит прямой проводник с током А. Определите индукцию поля в центре кольца (среда – воздух).
Магнитная индукция в центре кругового тока: Индукция магнитного поля в центре кольца будет равна их векторной сумме: Поскольку векторы или Ответ: Напряженность магнитного поля А/м. В этом поле находится плоская рамка площадью см2, которая может свободно вращаться. Плоскость рамки вначале совпадала с направлением поля. Затем по рамке кратковременно пропустили ток А и рамка получила угловое ускорение 1/с2. Считая вращающий момент постоянным, найти момент инерции рамки.
В общем случае на рамку действуют два момента: По условию, плоскость рамки вначале совпадала с направлением поля, поэтому в нашем случае Получим: Магнитный момент рамки: Тогда равенство моментов сил можно записать в виде: Окончательно момент инерции рамки (учтя, что
Ответ: Альфа-частица, пройдя ускоряющую разность потенциалов, стала двигаться в однородном магнитном поле о индукцией мТл по винтовой линии с шагом см и радиусом см. Определить ускоряющую разность потенциалов, которую прошла α-частица.
На α-частицу действует магнитная сила (благодаря нормальной составляющей скорости): Выразим радиус окружности Вдоль силовых линий поля магнитная сила не действует, поэтому частица движется прямолинейно с постоянной скоростью В результате суперпозиции двух движений α-частица будет двигаться по винтовой линии радиусом С учетом формул всех полученных выражений, уравнение для нахождения скорости влёта α-частицы в магнитное поле принимает вид:
Тогда Подставим числовые значения, получим: Ответ: В магнитное поле помещена квадратная рамка из алюминиевого провода с поперечным сечением мм2. Плоскость рамки перпендикулярна линиям индукции магнитного поля. Сторона рамки см. Какое количество теплоты выделится в рамке за время с, если магнитное поле, пронизывающее рамку, будет возрастать пропорционально времени, где Тл/c? Решение: По закону Джоуля-Ленца. Если ток проходит по неподвижному проводнику, то вся работа идет на его нагревание и количество теплоты, выделяющееся в участке цепи за время Сила тока есть скалярная физическая величина, определяемая зарядом, проходящем через поперечное сечение проводника в единицу времени: Магнитный поток, пронизывающий рамку Тогда окончательно количество теплоты, выделившееся в рамке за время
Ответ: Молекулярная физика
|






 Решение: Каждый из зарядов создаёт в центре треугольника электростатическое поле, напряжённость которого направлена от заряда, создающего поле т.к. заряды положительные. Пусть напряжённость поля первого заряда
Решение: Каждый из зарядов создаёт в центре треугольника электростатическое поле, напряжённость которого направлена от заряда, создающего поле т.к. заряды положительные. Пусть напряжённость поля первого заряда 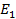 , второго заряда –
, второго заряда –  , третьего –
, третьего –  В силу условий задачи величины напряженности равны, так как равны заряды, создающие поле и расстояния от зарядов в вершинах до центра треугольника – тоже одинаковы (равны радиусу описанной окружности):
В силу условий задачи величины напряженности равны, так как равны заряды, создающие поле и расстояния от зарядов в вершинах до центра треугольника – тоже одинаковы (равны радиусу описанной окружности):  (в равностороннем треугольнике все высоты, медианы и биссектрисы пересекаются в одной точке (центре), которая делит их в отношении 1:2):
(в равностороннем треугольнике все высоты, медианы и биссектрисы пересекаются в одной точке (центре), которая делит их в отношении 1:2): 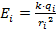 .
. В/м.
В/м. подчиняется принципу суперпозиции. Учтём, что напряжённости полей
подчиняется принципу суперпозиции. Учтём, что напряжённости полей  ; в скалярной форме:
; в скалярной форме:  , так как соответствующие вектора напряженностей не расположены вдоль одной прямой.
, так как соответствующие вектора напряженностей не расположены вдоль одной прямой. .
. ;
; 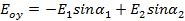
 .
. В/м.
В/м. ;
;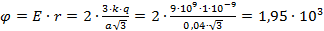 В.
В. В/м;
В/м;  В.
В. , откуда искомая разность потенциалов двух точек вдоль силовой линии:
, откуда искомая разность потенциалов двух точек вдоль силовой линии:  , где
, где  – расстояние между этими точками.
– расстояние между этими точками. , получим:
, получим: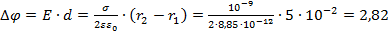 В.
В. В.
В. , где
, где  – элементарный заряд.
– элементарный заряд.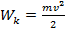 , силы электрического поля должны совершить работу
, силы электрического поля должны совершить работу 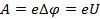 .
. , то
, то  , откуда скорость, с которой электрон достигнет другой пластины
, откуда скорость, с которой электрон достигнет другой пластины  м/с.
м/с. . По второму закону Ньютона
. По второму закону Ньютона 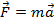 .
. от одной пластины конденсатора до другой, то:
от одной пластины конденсатора до другой, то:  . Тогда время прохождения равно:
. Тогда время прохождения равно:  , окончательно время движения электрона:
, окончательно время движения электрона:  с.
с. , кроме того напряжённость выражается соотношением:
, кроме того напряжённость выражается соотношением:  .
. Кл/м2.
Кл/м2.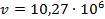 м/с; б)
м/с; б)  с; в)
с; в)  Кл/м2.
Кл/м2. Ом,
Ом,  Ом,
Ом, 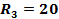 Ом,
Ом,  В. Гальванометр регистрирует ток
В. Гальванометр регистрирует ток  мА, идущий в направлении, указанном стрелкой. Определить ЭДС второго элемента
мА, идущий в направлении, указанном стрелкой. Определить ЭДС второго элемента  . Сопротивлением гальванометра и внутренним сопротивлением элементов пренебречь.
. Сопротивлением гальванометра и внутренним сопротивлением элементов пренебречь. Решение: Задача дана для расчета разветвленных цепей, когда в них есть несколько источников тока. При решении задач такого типа рационально пользоваться законами Кирхгофа.
Решение: Задача дана для расчета разветвленных цепей, когда в них есть несколько источников тока. При решении задач такого типа рационально пользоваться законами Кирхгофа. – нижний узел под
– нижний узел под  и слева от
и слева от  , В – средний узел слева от
, В – средний узел слева от  ,
,  – верхний узел слева от
– верхний узел слева от  ,
,  – верхний узел справа от
– верхний узел справа от  ,
,  – средний узел между
– средний узел между  – нижний узел под гальванометром и справа от
– нижний узел под гальванометром и справа от  (в данной схеме их три) и число узлов
(в данной схеме их три) и число узлов  (в данной схеме их один – в точках В и К).
(в данной схеме их один – в точках В и К).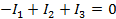 , для узла К:
, для узла К:  .
. .
. и
и  .
. .
. . Знаки при ЭДС устанавливаем в соответствии с ранее приведенными правилами (идём по часовой стрелке):
. Знаки при ЭДС устанавливаем в соответствии с ранее приведенными правилами (идём по часовой стрелке):  .
. и
и  ):
):


 .
. и подставим в четвертое, получим:
и подставим в четвертое, получим:  ;
; А.
А. А.
А.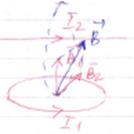 Решение: Прямолинейный бесконечно длинный проводник с током
Решение: Прямолинейный бесконечно длинный проводник с током  создает на расстоянии
создает на расстоянии  от своей оси магнитное поле индукцией
от своей оси магнитное поле индукцией  , направление которого можно определить по правилу буравчика (правого винта).
, направление которого можно определить по правилу буравчика (правого винта). .
. .
. и
и 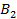 составляют между собой прямой угол, то
составляют между собой прямой угол, то  ,
, Тл.
Тл. Тл.
Тл. Решение: Индукция В внешнего поля может быть найдена из условия равновесия рамки в поле. Рамка будет находиться в равновесии, если сумма механических моментов, действующих на нее, будет рана нулю:
Решение: Индукция В внешнего поля может быть найдена из условия равновесия рамки в поле. Рамка будет находиться в равновесии, если сумма механических моментов, действующих на нее, будет рана нулю:  .
. – момент сил, с которым внешнее магнитное поле действует на рамку с током,
– момент сил, с которым внешнее магнитное поле действует на рамку с током,  – момент упругих сил, возникающих при закручивании нити, на которой рамке подвешена. Следовательно, формула для равновесия может быть переписана в виде:
– момент упругих сил, возникающих при закручивании нити, на которой рамке подвешена. Следовательно, формула для равновесия может быть переписана в виде:  .
. .
. , где
, где  – угол между нормалью к плоскости рамки и направлением линий индукции магнитного поля,
– угол между нормалью к плоскости рамки и направлением линий индукции магнитного поля,  – момент инерции рамки и
– момент инерции рамки и  – её угловое ускорение.
– её угловое ускорение. , где
, где  – сила тока в рамке;
– сила тока в рамке; 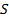 – площадь рамки,
– площадь рамки,  – число витков.
– число витков.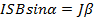 или
или  .
. ):
): кг∙м2.
кг∙м2. кг∙м2.
кг∙м2. Решение: В задаче рассматривается явление действия магнитного поля на движущийся в нем заряд. Скорость влетающей в однородное магнитное поле α-частицы
Решение: В задаче рассматривается явление действия магнитного поля на движущийся в нем заряд. Скорость влетающей в однородное магнитное поле α-частицы  разложим на две составляющие: тангенциальную
разложим на две составляющие: тангенциальную  , параллельную линиям индукции магнитного поля и нормальную
, параллельную линиям индукции магнитного поля и нормальную 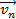 , перпендикулярную им,
, перпендикулярную им,  ,
,  .
. . Под действием этой силы α-частица будет двигаться по окружности радиуса
. Под действием этой силы α-частица будет двигаться по окружности радиуса  , который можно найти из условия:
, который можно найти из условия:  , так как сила Лоренца является центростремительной силой.
, так как сила Лоренца является центростремительной силой. , где
, где 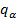 – модуль заряда α-частицы;
– модуль заряда α-частицы;  – индукция магнитного поля. Отсюда найдём скорость
– индукция магнитного поля. Отсюда найдём скорость  . Тогда
. Тогда  .
. :
:  , где
, где  .
.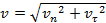 .
. ;
;  , тогда
, тогда  , где
, где  и
и  кг. Тогда окончательно ускоряющую разность потенциалов, которую прошла α-частица найдём из следующего соотношения:
кг. Тогда окончательно ускоряющую разность потенциалов, которую прошла α-частица найдём из следующего соотношения:  (по закону сохранения энергии).
(по закону сохранения энергии). .
. В.
В. В.
В. :
: 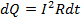 , где
, где  – сопротивление однородного проводника, в формуле которого
– сопротивление однородного проводника, в формуле которого  – удельное сопротивление вещества проводника (алюминий);
– удельное сопротивление вещества проводника (алюминий);  – его длина;
– его длина;  .
. будет (по условию
будет (по условию  ):
):  . Так как площадь рамки
. Так как площадь рамки  , то поток запишется:
, то поток запишется:  .
. найдём следующим образом:
найдём следующим образом:  .
. Дж.
Дж. Дж.
Дж.


