Множества и операции над ними. Числовые множества.
№1. Разделить многочлен P(x)=6x6-4x5+2x3-3 на многочлен Q(x)=x2-x+2. №2. Разделить многочлен P(x)=2x4-x+1 на линейный многочлен Q(x)=x+3, пользуясь схемой Горнера. №3. Разложить многочлен P(x)=x5-3x4-3x3-23x2-54x-30 на множители на множестве комплексных чисел. ---------------------------------------------------------------------------------------------------------------- Многочлены. Стр.2 Множества и операции над ними. Числовые множества.
Множество – одно из важнейших понятий математики. Вводится аксиоматически и не может быть определено через какие-либо элементарные понятия. Под множеством понимается совокупность вполне различаемых объектов произвольной природы, рассматриваемых как единое целое. Отдельные объекты, из которых состоит множество, называются элементами множества. О множестве можно говорить только в том случае, когда элементы множества различимы между собой. Например, нельзя говорить о множестве капель воды в стакане. Множество считается заданным, если о каждом элементе можно однозначно сделать вывод о том, входит или не входит этот элемент в рассматриваемое множество. Общим обозначением множества служит пара фигурных скобок { }, внутри которых перечисляются или описываются элементы множества. Для обозначения конкретных множеств используют заглавные латинские буквы A, B, C, X, …. Для обозначения элементов множества используют строчные буквы: a, b, c …. Если элемент а принадлежит множеству А, то пишут a Î A; если элемент а не принадлежит множеству А, то пишут a Ï A. Задать множество – значит описать множество всех его элементов. Способы задания множеств. 1. Перечисление. В этом случае необходимо перечислить все элементы, составляющие множество. Например, L={0, 1, 2, 3, 4, 5, 6, 7, 8, 9} – множество цифр десятичной системы счисления. Порядок записи элементов множества не имеет значения. Множество, задаваемое перечислением, не может содержать одинаковых элементов. 2. Описание. В этом случае необходимо указать условное обозначение элементов множества и характеристическое свойство, т.е. свойство, которым обладают все элементы только этого множества. При этом если A состоит из элементов x, для которых выполняется свойство P (x), то пишут Например, Числовые множества. Множество натуральных чисел состоит из чисел, которые получаются в результате счёта целых предметов, т.е. Натуральные числа, числа, им противоположные по знаку, и нуль составляют множество целых чисел, т.е. Множество чисел вида ---------------------------------------------------------------------------------------------------------------- Множества. Стр 1. Числа, которые нельзя представить в виде соотношения Совокупность множеств рациональных и иррациональных чисел представляет собой множество действительных чисел ( Среди натуральных чисел различают: · простые числа — это числа, которые делятся только на себя и на 1; · составные числа — это числа, которые делятся не только на себя и на 1; · число 1 не относится ни к простым, ни к составным числам; · взаимно простые числа — это числа, не имеющие общих делителей; · наименьшее общее кратное нескольких чисел (НОК) — это наименьшее натуральное число, которое делится на все эти числа; · наибольший общий делитель нескольких чисел (НОД) — это наибольшее натуральное число, на которое делятся все эти числа. Все множества в зависимости от числа входящих в них элементов можно разделить на конечные, бесконечные и пустые. Множество называется конечным, если число его элементов конечно, т.е. если существует натуральное число n, которое определяет число элементов множества. Например, Множество называется бесконечным, если оно содержит бесконечное число элементов. Например, Множество, которое не имеет элементов, называется пустым и обозначается символом Æ. Например, Множества А и В называются равными (А=В), если каждый элемент множества А принадлежит множеству В и каждый элемент множества В принадлежит множеству А, т.е. множества состоят из одних и тех же элементов. Если каждый элемент множества A есть элемент множества B, то множество A называется подмножеством множества B (или говорят, что A включено в B), пишут A Ì B (или B É A). Множества часто изображают диаграммами (кругами) Эйлера-Венна (рис. 1.1).
Рис. 1.1 Операции над множествами. К основным операциям над множествами относят пересечение, объединение, разность. Пересечением множеств A и B называется множество A Ç B, состоящее из всех элементов, которые принадлежат одновременно обоим множествам (рис. 1.2). ---------------------------------------------------------------------------------------------------------------- Множества. Стр 2. Объединением множеств A и B называется множество A È B, состоящее из всех тех элементов, которые принадлежат хотя бы одному из этих множеств (рис. 1.3). Разностью множества А и множества В называется множество A \ B, состоящее из всех элементов, которые принадлежат множеству A и не принадлежат множеству B (рис. 1.4).
A Ì B A Ç B A È B А \ В Рис. 1.1 Рис. 1.2 Рис. 1.3 Рис. 1.4
Для рассмотренных числовых множеств верны соотношения:
Произведение первых n натуральных чисел называется факториалом, для него введен специальный символ: По определению принимают 0! = 1.
Для всякого
Если
Пример 1. Даны два конечных числовых множества Решение. Выполняем операции над множествами по их определениям:
---------------------------------------------------------------------------------------------------------------- Множества. Стр 3. Пример 2. Дано Решение.
Пример 3. Сократить дробь Решение. Выделим общий множитель в числителе и знаменателе. Очевидно, что
Поэтому Пример 4. Вычислить сумму Решение. Получим последовательно слагаемые, придавая значения 1, 2, …, 7:
Вычисляя, приходим к ответу
|

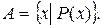
 .
.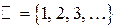 .
. .
.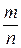 , где m – целое число, а n – натуральное, является множеством рациональных чисел, т.е.
, где m – целое число, а n – натуральное, является множеством рациональных чисел, т.е.  .
. ).
). .
. .
. .
.




 ;
;  ;
;  .
. .
. определены следующие понятия:
определены следующие понятия: целая часть (антье) числа x, определяется как целое число такое, что
целая часть (антье) числа x, определяется как целое число такое, что  ;
;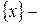 дробная часть (мантисса), определяется равенством
дробная часть (мантисса), определяется равенством  ;
; – знак числа (сигнум), определяется следующим образом:
– знак числа (сигнум), определяется следующим образом: 
 некоторые действительные числа, то сумму этих величин обозначают с использованием знака суммы:
некоторые действительные числа, то сумму этих величин обозначают с использованием знака суммы:  , где k – индекс суммирования.
, где k – индекс суммирования. и
и  . Записать элементы множеств
. Записать элементы множеств  ,
,  ,
,  ,
,  .
. ;
; ;
; ;
;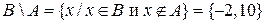 .
. . Найти
. Найти  ,
,  ,
,  .
.
 .
.









