Семестр № 3
1. Определение кратных интегралов и их интерпретации. 2. Определение криволинейных интегралов и их интерпретации. 3. Формула Грина и её следствия. 4. Определение поверхностных интегралов и их интерпретации. 5. Формулы Стокса и Остроградского, их векторная запись и физический смысл. 6. Основные определения теории поля. 7. Определение числового ряда. Определение частичной суммы ряда. 8. Определение сходящегося числового ряда. Критерий Коши. 9. Свойства сходящихся рядов. 10. Необходимый признак сходимости ряда. Гармонический ряд. 11. Признак сравнения. Предельная форма признака сравнения. 12. Признак Даламбера. Радикальный признак Коши. Интегральный признак Коши. 13. Понятие знакопеременных и знакочередующихся рядов. 14. Теорема Лейбница. Абсолютная и условная сходимость знакочередующихся рядов. 15. Понятие функционального ряда. Определение правильной сходимости функционального ряда. Свойства правильно сходящихся рядов. 16. Степенной ряд. Теорема Абеля. Область сходимости степенного ряда. Правило нахождения радиуса сходимости. 17. Свойства степенных рядов. 18. Применение дифференцирования и интегрирования степенных рядов для разложения функции в ряд. 19. Приближенные вычисления с помощью степенных рядов. 20. Тригонометрический ряд Фурье для 2p - и 2 l – периодических функций. 21. Условия разложения функции в ряд Фурье. 22. Ряд Фурье для четных и нечетных функций. 23. Переход от ряда Фурье к интегралу Фурье. Интеграл Фурье для четных и нечетных функций.
Образцы задач для контрольных, зачетных и экзаменационных работ
1. Вычислить пределы: 2.Вычислить производную функции: 3.Найти касательную прямую и нормаль, проведенные в точке А (1,1) к графику функции, заданной неявно уравнением 4. Найти дифференциал функции 5.Найти участки возрастания и убывания и точки экстремума функции 6.Найти асимптоты графика функции 7.Провести полное исследование и нарисовать эскиз графика функции 8.Разложить функцию 9.Разложить по формуле Маклорена до о(хn) функции: 10.Вычислить пределы с помощью формулы Маклорена: Вычислить предел или доказать, что он не существует: 11.Выяснить, будет ли функция 12.Найти частные производные первого порядка для функций: 13.Найти первый дифференциал функции 14.Найти производную функции 15.Исследовать на экстремум функцию 16.Найти экстремумы функции 17.Вычислить неопределенные интегралы: 18.Вычислить определенные интегралы: 19.Найти сумму ряда Исследовать на сходимость числовые ряды 20 – 23: 20. 21. 23. 24. Будет ли данный ряд 25. Исследовать на сходимость знакочередующийся ряд 26. Найти предельную функцию для функциональной последовательности 27. Доказать, что ряд 28. Пользуясь признаком Вейерштрасса, доказать равномерную сходимость ряда 29. Найти множества всех значений x, при которых функция 30. Найти области сходимости и расходимости функционального ряда 31. Найти радиус сходимости, области сходимости и расходимости степенного ряда 32. Разложить функцию 39. Разложить в ряд Маклорена функцию 40. Найти функцию
|

 ; б)
; б)  .
. ; б)
; б)  .
. .
. , заданной параметрически:
, заданной параметрически:  в точке А, соответствующей значению параметра
в точке А, соответствующей значению параметра 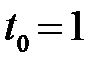 .
. . Найти наибольшее и наименьшее значения этой функции на отрезке [1,4].
. Найти наибольшее и наименьшее значения этой функции на отрезке [1,4]. .
. .
. по формуле Тейлора в окрестности точки
по формуле Тейлора в окрестности точки  до
до  .
. ; б)
; б)  .
. ; б)
; б)  .
.
 ; б)
; б)  .
. непрерывной в точке (0,0). Ответ обосновать.
непрерывной в точке (0,0). Ответ обосновать. ; б)
; б)  .
. в точке (1,0,1).
в точке (1,0,1). в точке А (1,1,0) по направлению вектора
в точке А (1,1,0) по направлению вектора  , где М (2,4,5), N (1,2,3).
, где М (2,4,5), N (1,2,3). .
. при условии
при условии  .
. ; б)
; б)  .
. ; б)
; б)  .
. .
.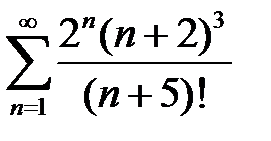 .
. .
. .
. :
:  .
. на множестве
на множестве  .
. не является равномерно сходящимся на множестве
не является равномерно сходящимся на множестве  .
. на множестве
на множестве  .
. :
:  .
. .
. в ряд Тейлора в окрестности точки x 0= –1. Найти интервал сходимости этого ряда.
в ряд Тейлора в окрестности точки x 0= –1. Найти интервал сходимости этого ряда. .
. , если
, если  .
.


