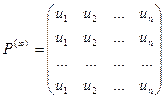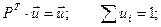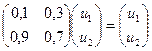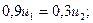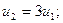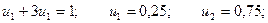Определение. процесс функционирования системы массового обслуживания называется случайным процессом.
Чтобы оптимизировать процесс функционирования системы массового обслуживания его надо изучить и описать математически. Теория массового обслуживания является очень быстро развивающимся разделом теории вероятностей, т.к. ее применение на практике чрезвычайно широко.
Случайный процесс, протекающий в системе массового обслуживания состоит в том, что система в случайные моменты времени переходит из одного состояния в другое. Меняется число заявок, число занятых каналов, число заявок в очереди и проч.
Определение. Если переход системы из одного состояния в другое происходит скачком, а количество состояний системы (конечное или бесконечное) можно пронумеровать, то такая система называется системой дискретного типа.
Если количество возможных состояний счетно, то сумма вероятностей нахождения системы в одном из состояний равна 1.
Совокупность вероятностей pk (t) для каждого момента времени характеризует данное сечение случайного процесса. Случайные процессы со счетным множеством состояний бывают двух типов: c дискретным или непрерывным временем. Если переходы системы из одного состояния в другое могут происходить только в строго определенные моменты времени, то случайный процесс будет процессом с дискретным временем, а если переход возможен в любой момент времени, то процесс будет процессом с непрерывным временем. Поскольку в реальности заявки на систему массового обслуживания могут поступать в любой момент времени, то большинство реальных систем массового обслуживания будут системами с процессом с непрерывным временем. Для того, чтобы описать случайный процесс в системе с непрерывным временем необходимо прежде всего проанализировать причины, вызывающие изменение состояния системы. Эти причины определяются потоком заявок, поступающих на систему.
Поток событий.
Определение. Потоком событий называется последовательность событий, происходящих один за другим в какие- то моменты времени.
Характер событий, образующих поток может быть различным, а если события отличаются друг от друга только моментом времени, в который они происходят, то такой поток событий называется однородным. Однородный поток можно изобразить последовательностью точек на оси, соответствующей времени:
t1 t2 tn
t
Определение. Поток событий называется регулярным, если события следует одно за другим через строго определенные промежутки времени.
Определение. Поток событий называется стационарным, если вероятность попадания того ли иного числа событий на участок времени t зависит только от длины участка и не зависит от того, где именно на оси расположен этот участок. Стационарность потока событий означает, что плотность потока постоянна, отсутствуют промежутки времени, в течение которых событий больше чем обычно. Классический пример – “час пик” на транспорте.
Определение. Поток событий называется потоком без последействий, если для любых неперекрещивающихся участков времени число событий, попадающих на один из них, не зависит от числа событий, опадающих на другие. Отсутствие последействий означает, что заявки в систему поступают независимо друг от друга. Поток выходных событий систем массового обслуживания обычно имеет последействие, даже если входной поток его не имеет. Пример – вход пассажиров на станцию метро – поток без последействия, т.к. причины прихода отдельного пассажира не связаны с причинами прихода всех остальных, а выход пассажиров со станции – поток с последействием, т.к. он обусловлен прибытием поезда. Последействие, свойственное выходному потоку следует учитывать, если этот поток в свою очередь является входным для какой- либо другой системы.
Определение. Поток событий называется ординарным, если вероятность попадания на элементарный участок D t двух или более событий достаточно мало по сравнению с вероятностью попадания одного события. Условие ординарности означает, что заявки на систему приходят по одному, а не парами, тройками и т.д. Однако, если заявки поступают только парами, только тройками и т.д., то такой поток легко свести к ординарному.
Определение. Если поток событий стационарен, ординарен и без последействий, то такой поток называется простейшим (пуассоновским) потоком. Это название связано с тем, что в этом случае число событий, попадающих на любой фиксированный интервал времени, распределено по распределению Пуассона.
В соответствии с этим законом распределения математическое ожидание числа точек, попавших попадающих на участок времени t, имеет вид:
l - плотность потока – среднее число событий в единицу времени.
Вероятность того, что за время t произойдет ровно т событий, равна
Вероятность того, что в течение данного времени не произойдет ни одного события, равна:
Пусть Т – промежуток времени между двумя произвольными соседними событиями в простейшем потоке. Найдем функцию распределения
В соответствии с законом распределения Пуассона, получаем:
Математическое ожидание, дисперсия и среднее квадратическое отклонение этой величины соответственно равны:
Таким образом, для величины Т получили показательный закон распределения.
Пример. В бюро обслуживания в среднем поступает 12 заявок в час. Считая поток заказов простейшим, определить вероятность того, что: а) за 1 минуту не поступит ни одного заказа, б) за 10 минут поступит не более трех заказов.
Сначала найдем плотность (интенсивность) потока, выразив ее в количестве заявок в минуту. Очевидно, эта величина равна Далее находим вероятность того, что за время t = 1 мин не поступит ни одной заявки по формуле:
Вероятность того, что за 10 минут поступит не более трех заказов будет складываться из вероятностей того, что не поступит ни одного заказа, поступит один, два или ровно три заказа.
Пример. В ресторан прибывает в среднем 20 посетителей в час. Считая поток посетителей простейшим, и зная, что ресторан открывается в 11.00, определите: а) вероятность того, что в 11.12 в ресторан придет 20 посетителей при условии, что в 11.07 их было 18 б) вероятность того, что между 11.28 и 11.30 в ресторане окажется новый посетитель, если известно, что предшествующий посетитель прибыл в 11.25.
Для ответ на первый вопрос фактически надо найти вероятность того, что в промежуток от 11.07 до 11.12 (t = 5 минут) придет ровно 2 посетителя. При этом мы знаем интенсивность потока посетителей - l = 20/60 = 1/3 посетителей в минуту. Конечно, данная величина носит условный характер, т.к. посетители не могут приходить по частям. Искомая вероятность равна:
Теперь перейдем ко второму вопросу. Нам не сказано, сколько именно новых посетителей будет в промежутке от 11.28 до 11.30, главное чтобы был хоть один. Эта вероятность равна
Если поток событий нестационарен, то его плотность l уже не является постоянной величиной, а зависит от времени.
Определение. Мгновенной плотностью потока событий называется предел отношения среднего числа событий, приходящегося на элементарный отрезок времени (t, t + Dt), к длине этого участка, которая стремиться к нулю.
Как видно из приведенного определения, с учетом того, что среднее число событий на участке времени равно математическому ожиданию, то можно сказать, что мгновенная плотность потока равна производной по времени от математического ожидания числа событий на участке (0, t).
Определение. Нестационарным пуассоновским потоком называется ординарный поток однородных событий без последействий с переменной плотностью l(t).
Для такого потока число событий, попадающих на участок длины t, начинающийся в точке t0, подчиняется закону Пуассона:
Здесь а – математическое ожидание числа событий на участке от t0 до t + t0. Оно вычисляется по формуле:
Величина а на только от длины участка t, но и от его положения во времени. Закон распределения промежутка Т между двумя соседними событиями также будет зависеть от того, где на временной оси расположено первое из событий, а также от функции l(t).
Тогда, соответственно, вероятность появления хотя бы одного события на этом интервале времени будет равна:
Плотность распределения можно найти дифференцированием:
Эта плотность распределения уже не будет показательной. Она зависит от параметра t0 и вида функции l(t). Однако, условие отсутствия последействия в этом виде потока сохраняется.
Поток Пальма.
Поток Пальма еще называют потоком с ограниченным последействием.
Определение. Потоком Пальма называется ординарный поток однородных событий, если промежутки между событиями Т1, Т2, … представляют собой независимые случайные величины.
Если промежутки времени Т1, Т2, … распределены по показательному закону, то поток Пальма становится простейшим потоком. Примером потока Пальма может служить движение колонны автомобилей. Пусть движется колонна автомобилей, каждый из которых, двигаясь с одинаковой скоростью, стремится держаться на некотором заданном расстоянии от впереди идущего автомобиля. Однако, вследствие воздействия множества случайных факторов, это расстояние выдерживается не точно. Тогда времена пересечения каждым автомобилем определенного рубежа Т1, Т2, … будут независимыми случайными величинами и образуют по ток Пальма. Отметим, что если автомобили будут стремиться выдерживать заданное расстояние не от соседней машины, а от головной, то моменты пересечения этого рубежа уже не будут образовывать поток Пальма. Поток Пальма часто получается в качестве выходного потока систем массового обслуживания.
Теорема. (Теорема Пальма) Пусть на систему массового обслуживания поступает поток заявок типа Пальма, причем заявка, заставшая все каналы занятыми, получает отказ (не обслуживается). Если при этом время обслуживания имеет показательный закон распределения, то поток не обслуженных заявок является также потоком типа Пальма.
Этот факт важен, так как на практике получившие отказ заявки обычно перенаправляются на другую систему массового обслуживания, т.е. образуют для этой системы входной поток. Так, если на систему массового обслуживания поступает простейший входной поток, то поток заявок, получивших отказ, уже не будет простейшим, однако, будет потоком с ограниченным последействием.
Потоки Эрланга.
Потоки Эрланга также являются потоками с ограниченным последействием. Они образуются просеиванием простейшего потока. Суть этого просеивания состоит в следующем. Если изобразить на временной оси простейший поток, поставив в соответствие каждому событию некоторую точку, и выбросить из потока каждую вторую точку, то получим поток Эрланга первого порядка. Оставив каждую третью точку и выбросив две промежуточные, получаем поток Эрланга второго порядка и т.д.
Определение. Потоком Эрланга k – порядка называется поток, получаемый из простейшего, если сохранить в простейшем потоке каждую (k + 1) – ю точку, а остальные выбросить.
Очевидно, что простейший поток может рассматриваться как поток Эрланга нулевого порядка.
Пусть имеется простейший поток с интервалами Т1, Т2, … между событиями. Величина Т – промежуток времени между двумя соседними событиями в потоке Эрланга k – го порядка. Очевидно, что
Обозначим fk(t) плотность распределения величины Т для потока Эрланга k – го порядка. Если умножить эту плотность на элементарный отрезок времени dt, мы получим вероятность того, что величина Т примет значение в некоторой сколь угодно малой окрестности точки t- (t, t + dt). На этот участок должна попасть конечная точка промежутка, а предыдущие k точек простейшего потока – на промежуток (0, t). Вероятность первого события равна
Полученный закон распределения называется законом распределением Эрланга k - го порядка. При k = 0 получаем показательный закон распределения.
Математическое ожидание, дисперсия и среднее квадратическое отклонение для распределения Эрланга находятся по формулам:
Плотность потока Эрланга равна
Для промежутка времени между двумя соседними событиями в потоке Т рассмотрим нормированную величину
Закон распределения для такого потока будет иметь вид:
Математическое ожидание и дисперсия будут равны:
Получается, что неограниченном увеличении k нормированный поток Эрланга приближается к регулярному потоку с постоянными интервалами, равными Изменение порядка нормированного потока Эрланга позволяет получить различную степень последействия. Последействие возрастает с увеличением k. На практике это удобно для приближенного представления реального потока с каким – либо последействием потоком Эрланга. При этом порядок этого потока определяется из того соображения, чтобы характеристики потока Эрланга (математическое ожидание и дисперсия) совпадали с характеристиками исходного потока.
Цепи Маркова.
(Андрей Андреевич Марков (1856-1922) – русский математик, академик)
Определение. Процесс, протекающий в физической системе, называется марковским, если в любой момент времени вероятность любого состояния системы в будущем зависит только от состояния системы в текущий момент и не зависит от того, каким образом система пришла в это состояние.
Определение. Цепью Маркова называется последовательность испытаний, в каждом из которых появляется только одно из k несовместных событий Ai из полной группы. При этом условная вероятность pij(s) того, что в s –ом испытании наступит событие Aj при условии, что в (s – 1) – ом испытании наступило событие Ai, не зависит от результатов предшествующих испытаний.
Независимые испытания являются частным случаем цепи Маркова. События называются состояниями системы, а испытания – изменениями состояний системы.
По характеру изменений состояний цепи Маркова можно разделить на две группы.
Определение. Цепью Маркова с дискретным временем называется цепь, изменение состояний которой происходит в определенные фиксированные моменты времени. Цепью Маркова с непрерывным временем называется цепь, изменение состояний которой возможно в любые случайные моменты времени.
Определение. Однородной называется цепь Маркова, если условная вероятность pij перехода системы из состояния i в состояние j не зависит от номера испытания. Вероятность pij называется переходной вероятностью.
Допустим, число состояний конечно и равно k. Тогда матрица, составленная из условных вероятностей перехода будет иметь вид:
Эта матрица называется матрицей перехода системы. Т.к. в каждой строке содержаться вероятности событий, которые образуют полную группу, то, очевидно, что сумма элементов каждой строки матрицы равна единице. На основе матрицы перехода системы можно построить так называемый граф состояний системы,его еще называют размеченный граф состояний. Это удобно для наглядного представления цепи. Порядок построения граф рассмотрим на примере.
Пример. По заданной матрице перехода построить граф состояний.
Т.к. матрица четвертого порядка, то, соответственно, система имеет 4 возможных состояния.
S1 0,2 0,7
S2 0,4 S4 0,6 0,5
0,1 0,5 S3
На графе не отмечаются вероятности перехода системы из одного состояния в то же самое. При рассмотрении конкретных систем удобно сначала построить граф состояний, затем определить вероятность переходов системы из одного состояния в то же самое (исходя из требования равенства единице суммы элементов строк матрицы), а потом составить матрицу переходов системы.
Пусть Pij(n) – вероятность того, что в результате n испытаний система перейдет из состояния i в состояние j, r – некоторое промежуточное состояние между состояниями i и j. Вероятности перехода из одного состояния в другое pij(1) = pij.
Тогда вероятность Pij(n) может быть найдена по формуле, называемой равенством Маркова:
Здесь т – число шагов (испытаний), за которое система перешла из состояния i в состояние r. В принципе, равенство Маркова есть ни что иное как несколько видоизменная формула полной вероятности. Зная переходные вероятности (т.е. зная матрицу перехода Р1), можно найти вероятности перехода из состояния в состояние за два шага Pij(2), т.е. матрицу Р2, зная ее – найти матрицу Р3, и т.д.
Непосредственное применений полученной выше формулы не очень удобно, поэтому, можно воспользоваться приемами матричного исчисления (ведь эта формула по сути – не что иное как формула перемножения двух матриц). Тогда в общем виде можно записать:
Вообще то этот факт обычно формулируется в виде теоремы, однако, ее доказательство достаточно простое, поэтому приводить его не буду.
Пример. Задана матрица переходов Р1. Найти матрицу Р3.
Определение. Матрицы, суммы элементов всех строк которых равны единице, называются стохастическими. Если при некотором п все элементы матрицы Рп не равны нулю, то такая матрица переходов называется регулярной.
Другими словами, регулярные матрицы переходов задают цепь Маркова, в которой каждое состояние может быть достигнуто через п шагов из любого состояния. Такие цепи Маркова также называются регулярными.
Теорема. (теорема о предельных вероятностях) Пусть дана регулярная цепь Маркова с п состояниями и Р – ее матрица вероятностей перехода. Тогда существует предел
Т.е. матрица состоит из одинаковых строк.
Теперь о величинах ui. Числа u1, u2, …, un называются предельными вероятностями. Эти вероятности не зависят от исходного состояния системы и являются компонентами собственного вектора матрицы РТ (транспонированной к матрице Р). Этот вектор полностью определяется из условий:
Пример. Найдем предельные вероятности для рассмотренного выше примера.
C учетом того, что u1 + u2 = 1, получаем:
Получаем:
D:\alex\studorgbaza10-19\lect1.DOC
|

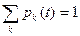

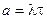

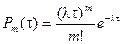
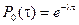
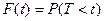

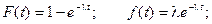
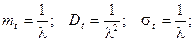
 .
.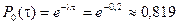
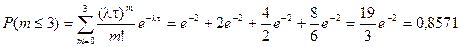

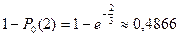 . Здесь Р0 (2) – вероятность того, что в этом промежутке не будет ни одного посетителя.
. Здесь Р0 (2) – вероятность того, что в этом промежутке не будет ни одного посетителя.

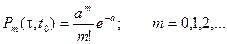
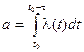

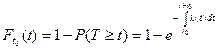

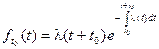
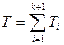 . Так как первоначальный поток – простейший, то случайные величины Т1, Т2, … распределены по показательному закону:
. Так как первоначальный поток – простейший, то случайные величины Т1, Т2, … распределены по показательному закону: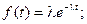
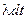 , а второго -
, а второго - 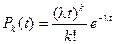 . Эти события должны осуществиться совместно, значит, их вероятности надо перемножить.
. Эти события должны осуществиться совместно, значит, их вероятности надо перемножить.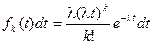

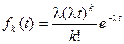


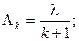
 . Такой поток будет называться нормированным потоком Эрланга.
. Такой поток будет называться нормированным потоком Эрланга.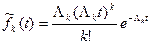 ,
, 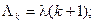
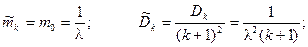
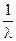 .
.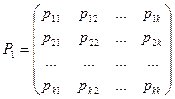
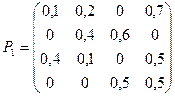


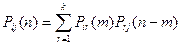

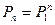
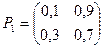

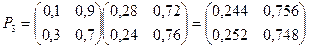
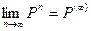 и матрица Р(¥) имеет вид:
и матрица Р(¥) имеет вид: