СТАЛЬНАЯ БАЛОЧНАЯ КЛЕТКА
СТАЛЬНАЯ БАЛОЧНАЯ КЛЕТКА 2.1. Расчёт настила Вычислим переводной модуль упругости:
Где
Для начала определим отношение наибольшего пролета настила к его высоте по уравнению А.Л. Телояна:
Где
По полученному отношению
Меняем длину настила, принимая её равной
Находим значение момента инерции расчётного сечения настила длиной
где Определяем прогиб настила лишь от поперечной нагрузки:
Рассчитаем цилиндрическую жёсткость полоски настила, т.е. изгибную жёсткость, когда поперечные деформации невозможны:
Находим коэффициент влияния продольной силы
Вычисляем предельный прогиб и сравниваем его с предельно допустимым значением:
Определяем величину распора:
Находим значение изгибающего момента от расчётной нагрузки на балку настила:
Определяем несущую способность настила и сравниваем её с предельно допустимым значением:
Где
Условие прочности настила выполняется.
2.2. Расчёт прокатных балок
Определим расчётный изгибающий момент в балке (без учёта массы самой балки):
Определим расчётный изгибающий момент в балке (без учёта массы самой балки):
По максимальному изгибающему моменту в балке определяем требуемый момент сопротивления ригеля:
По сортаменту (приложение 1) принимаем для расчёта двутавр №50 с Расчётное сечение балки включаем часть примыкающего настила, длину которого принимаем равной наименьшему из полученных значений:
Принимаем Площадь настила: Определим полную площадь ригеля: Смещение центра тяжести будет равно:
Определим момент инерции ригеля:
Определим минимальный момент сопротивления ригеля:
Определим расчётную нагрузку на балку с учётом собственной массы двутавра:
Определим максимальный момент с учётом веса двутавра:
Проверим условие прочности ригеля:
Условие прочности балок настила выполняется. Определим полную нормативную нагрузку на балку:
Определяем максимальный прогиб и сравниваем с предельно допустимым значением, принимая
Условие жёсткости балок настила выполняется.
|

 кН/см2
кН/см2 - модуль упругости, для стали
- модуль упругости, для стали  кН/см2
кН/см2 - коэффициент Пуассона, для стали
- коэффициент Пуассона, для стали 
 см
см – длина пролёта настила;
– длина пролёта настила; – толщина настила;
– толщина настила; – заданное отношение предельного прогиба к пролёту настила
– заданное отношение предельного прогиба к пролёту настила  , для настила
, для настила  ;
; – равномерно распределённая нагрузка на настил;
– равномерно распределённая нагрузка на настил; принимается толщина настила:
принимается толщина настила: см
см м и пересчитываем толщину настила:
м и пересчитываем толщину настила: см
см см по формуле:
см по формуле: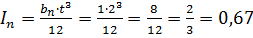

 см
см кН
кН 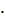 см2
см2

 см
см 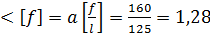 см
см кН
кН кН
кН  кН/см2
кН/см2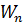 - момент сопротивления расчётного сечения настила
- момент сопротивления расчётного сечения настила кН/см2
кН/см2 кН/м
кН/м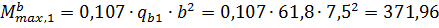 кН
кН  см3
см3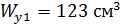 ;
; 
 ;
; 
 см
см см
см см
см см2
см2 см2
см2 см
см
 см4
см4 см3
см3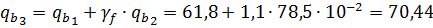 кН/м = 0,70 Н/см
кН/м = 0,70 Н/см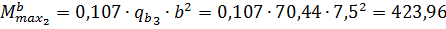 кН
кН  кН/см2
кН/см2 кН/м = 0,45 кН/см
кН/м = 0,45 кН/см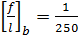
 см
см  см
см


