Тема. Средние величины и показатели вариации
В таблице представлено распределение магазинов по величине товарооборота за месяц. Определить среднюю величину товарооборота и остальные показатели задания.
Охарактеризовать ряд распределения с помощью следующих показателей: 1) Средняя величина анализируемого признака; 2) Размах вариации; 3) Среднее линейное отклонение; 4) Среднее квадратическое отклонение; 5) Дисперсия; 6) Коэффициент вариации; 7) Мода, медиана, первый и третий квартиль; 8) Коэффициент асимметрии; 9) Дать графическое изображение и выводы по результатам расчётов.
Решение: 1) Определим среднюю величину анализируемого признака ( Воспользуемся формулой средней арифметической взвешенной.
где
n – число единиц совокупности. Промежуточные расчеты представим в табл. 1.1. Таблица 1.1 Промежуточные расчеты для определения средней и показателей вариации
Таким образом, средний размер товарооборота магазинов за месяц составит 11 млн. руб. 2) Определим размах (R).
где R = 23 – 3 = 20 млн. руб. Таким образом, величина товарооборота магазинов за месяц колеблется от 3 до 20 млн. руб. 3) Определим среднее линейное отклонение (d).
Таким образом, средняя величина колеблемости величины товарооборота магазинов за месяц по среднему линейному отклонению составит 3,3 млн. руб. 4) Определим среднее квадратическое отклонение (
Таким образом, средняя величина колеблемости величины товарооборота магазинов за месяц по среднему квадратическому отклонению составит 4,1 млн. руб. 5) Определим дисперсию (
6) Определим коэффициент вариации (V).
Таким образом, совокупность магазинов по величине товарооборота за месяц не однородна, т.к. V > 33%. 7) Определим: а) моду (Мо).
где
Таким образом, в данной совокупности преобладают магазины с величиной товарооборота за месяц 10,4 млн. руб. б) медиану (Ме). Ме = где
Ме = Таким образом, в данной совокупности 50% магазинов имеют величину товарооборота за месяц менее 10,7 млн. руб., а 50% магазинов – более 10,7 млн. руб. в) первый (
где
где
Расчет квартилей позволяет отметить, что 25% магазинов имеют величину товарооборота за месяц менее 8,1 млн. руб., а 25% магазинов – свыше 13,6 млн. руб. Остальные 50% магазинов имеют величину товарооборота за месяц от 8,1 до 13,6 млн. руб. 8) Определим коэффициент асимметрии (Аs).
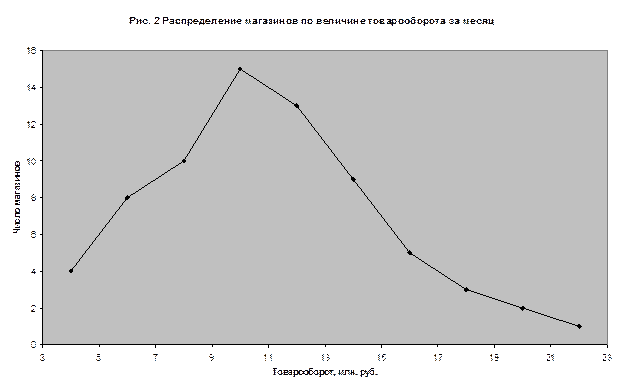
Это говорит о небольшой правосторонней асимметрии. 9) Изобразим ряд распределения графически. а) Построим гистограмму распределения.
б) Построим полигон распределения.
в) Построим кумуляту распределения.
|

 ).
).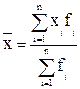 ,
, – значения осредняемого признака;
– значения осредняемого признака;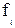 – частота;
– частота;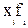




 =
=  = 11 млн. руб.
= 11 млн. руб. ,
, – наибольшее и наименьшее значения признака в исследуемой совокупности.
– наибольшее и наименьшее значения признака в исследуемой совокупности.
 = 3,3 млн. руб.
= 3,3 млн. руб. ).
).
 4,1 млн. руб.
4,1 млн. руб. ).
). = 16,43
= 16,43
 36,0%
36,0% ,
, – нижняя граница модального интервала;
– нижняя граница модального интервала; – величина интервала;
– величина интервала; – частота, соответствующая модальному интервалу;
– частота, соответствующая модальному интервалу; – предмодальная частота;
– предмодальная частота; – послемодальная частота.
– послемодальная частота. = 10,4 млн. руб.
= 10,4 млн. руб. ,
, – нижняя граница медианного интервала;
– нижняя граница медианного интервала; – накопленная частота интервала, предшествующая медианному интервалу;
– накопленная частота интервала, предшествующая медианному интервалу; – частота медианного интервала.
– частота медианного интервала. = 10,7 млн. руб.
= 10,7 млн. руб. ) и третий (
) и третий ( ) квартили.
) квартили. ,
, – нижняя граница первого квартильного интервала;
– нижняя граница первого квартильного интервала; – частота первого квартильного интервала.
– частота первого квартильного интервала. 8,1 млн. руб.
8,1 млн. руб. ,
, – нижняя граница третьего квартильного интервала;
– нижняя граница третьего квартильного интервала; – частота третьего квартильного интервала.
– частота третьего квартильного интервала. = 13,6 млн. руб.
= 13,6 млн. руб.
 > 0
> 0