Ответ. -3.
в) Найти Решение. Для раскрытия неопределенности
Ответ. г) Найти Решение. Для раскрытия неопределенности
Ответ. k д) Найти Решение. Для раскрытия неопределенности
Выделяем первый замечательный предел, то есть, умножаем числитель и знаменатель на
Ответ.
е) Найти Решение. Для раскрытия неопределенности
Ответ. ж) Найти Решение. Для раскрытия неопределенности
Ответ. Найти Решение. Подставим значение
Ответ. 2. Задана функция Требуется: - найти пределы функции при приближении к каждому из данных значений - установить является ли данная функция непрерывной или разрывной для каждого из данных значений - сделать схематический чертеж. Решение. Найдем левый и правый пределы в точке
Левый предел конечен и равен 0, а правый предел бесконечен. Следовательно, по определению Найдем левый и правый пределы в точке
Сделаем схематический чертеж.
Рис. 1 3. Функция задается различными аналитическими выражениями для различных областей независимой переменной. Требуется:
|

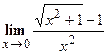 .
. в этом случае, нужно умножить числитель и знаменатель на выражение, сопряженное числителю, а затем сократить дробь на общий множитель.
в этом случае, нужно умножить числитель и знаменатель на выражение, сопряженное числителю, а затем сократить дробь на общий множитель.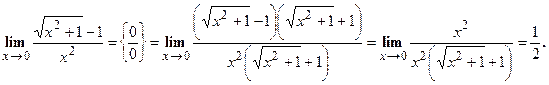
 .
. .
.

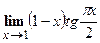 .
.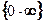 в этом случае, нужно произведение преобразовать в частное, то есть неопределенность
в этом случае, нужно произведение преобразовать в частное, то есть неопределенность  .
.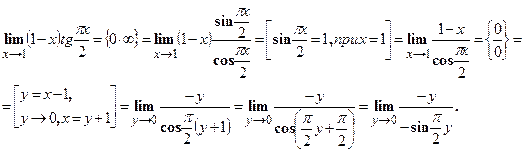
 . Получаем,
. Получаем, .
. .
. .
. в этом случае, нужно выделить второй замечательный предел:
в этом случае, нужно выделить второй замечательный предел:  .
.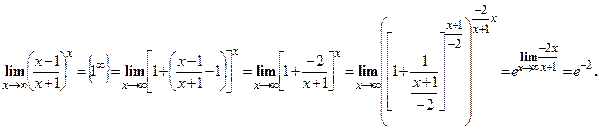
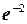 .
.
 в этом случае, нужно выделить второй замечательный предел:
в этом случае, нужно выделить второй замечательный предел: 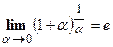 .
.
 .
.
 в функцию, стоящую под знаком предела. Получим,
в функцию, стоящую под знаком предела. Получим,
 .
.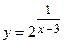 и два значения аргумента
и два значения аргумента  .
. слева и справа;
слева и справа; .
.

 .
.
 , т.е.
, т.е. 



