· Уравнение гармонических колебаний:
 ,
,
где  – смещение точки от положения равновесия; А – амплитуда колебаний;
– смещение точки от положения равновесия; А – амплитуда колебаний;  – круговая (циклическая частота); t – время;
– круговая (циклическая частота); t – время;  – начальная фаза колебаний.
– начальная фаза колебаний.
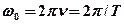 ,
,
где  – частота колебаний,
– частота колебаний,  – период колебаний.
– период колебаний.
· Скорость и ускорение при гармонических колебаниях:
 ,
,
 .
.
· Возвращающая сила:
 ,
,
 ,
,
где  – коэффициент упругой (квазиупругой) силы;
– коэффициент упругой (квазиупругой) силы;  – масса материальной точки.
– масса материальной точки.
· Максимальная возвращающая сила
 .
.
· Кинетическая энергия колеблющейся точки
 .
.
· Потенциальная энергия колеблющейся точки
 .
.
· Полная энергия при гармонических колебаниях:
 .
.
· Периоды колебаний:
 – математический маятник (
– математический маятник ( – длина нити;
– длина нити;  – ускорение свободного падения),
– ускорение свободного падения),
 – пружинный маятник (
– пружинный маятник ( – масса тела;
– масса тела;  – жесткость пружины),
– жесткость пружины),
 – физический маятник (
– физический маятник ( – момент инерции тела относительно оси, проходящей через точку подвеса;
– момент инерции тела относительно оси, проходящей через точку подвеса;  – масса тела;
– масса тела;  – расстояние от точки подвеса до центра масс).
– расстояние от точки подвеса до центра масс).
· Уравнение затухающих колебаний:
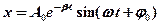 ,
,
где  – амплитуда колебаний в начальный момент времени;
– амплитуда колебаний в начальный момент времени;  – амплитуда затухающих колебаний;
– амплитуда затухающих колебаний;  – коэффициент затухания (
– коэффициент затухания ( – коэффициент сопротивления;
– коэффициент сопротивления;  – масса точки);
– масса точки);  – частота затухающих колебаний.
– частота затухающих колебаний.
· Логарифмический декремент затухания
 .
.
· Амплитуда результирующего колебания, полученного при сложении двух колебаний одинаковой частоты и одного направления:
 ,
,
где  и
и  – амплитуды слагаемых колебаний;
– амплитуды слагаемых колебаний;  – разность фаз слагаемых колебаний.
– разность фаз слагаемых колебаний.
· Начальная фаза результирующего колебания определяется из формулы:

 .
.
· Уравнение траектории точки, участвующей в двух взаимно перпендикулярных колебаниях с одинаковыми частотами:
 ,
,
где  – разность фаз складываемых колебаний.
– разность фаз складываемых колебаний.

 ,
, – смещение точки от положения равновесия; А – амплитуда колебаний;
– смещение точки от положения равновесия; А – амплитуда колебаний;  – круговая (циклическая частота); t – время;
– круговая (циклическая частота); t – время;  – начальная фаза колебаний.
– начальная фаза колебаний.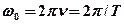 ,
, – частота колебаний,
– частота колебаний,  – период колебаний.
– период колебаний. ,
, .
. ,
, ,
, – коэффициент упругой (квазиупругой) силы;
– коэффициент упругой (квазиупругой) силы;  – масса материальной точки.
– масса материальной точки. .
. .
. .
. .
. – математический маятник (
– математический маятник ( – длина нити;
– длина нити;  – ускорение свободного падения),
– ускорение свободного падения), – пружинный маятник (
– пружинный маятник ( – жесткость пружины),
– жесткость пружины), – физический маятник (
– физический маятник ( – момент инерции тела относительно оси, проходящей через точку подвеса;
– момент инерции тела относительно оси, проходящей через точку подвеса;  – расстояние от точки подвеса до центра масс).
– расстояние от точки подвеса до центра масс).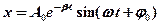 ,
, – амплитуда колебаний в начальный момент времени;
– амплитуда колебаний в начальный момент времени;  – амплитуда затухающих колебаний;
– амплитуда затухающих колебаний;  – коэффициент затухания (
– коэффициент затухания ( – коэффициент сопротивления;
– коэффициент сопротивления;  – частота затухающих колебаний.
– частота затухающих колебаний. .
. ,
, и
и  – амплитуды слагаемых колебаний;
– амплитуды слагаемых колебаний;  – разность фаз слагаемых колебаний.
– разность фаз слагаемых колебаний.
 .
. ,
, – разность фаз складываемых колебаний.
– разность фаз складываемых колебаний.


