Тригонометрия.
Формулы понижения степеней тригонометрических функций.
Тригонометрические формулы половинного аргумента.
Таблица некоторых значений тригонометрических функций.
Знаки тригонометрических функций.
II I II I + + x – + x
– – – +
y
– + x + – III IV Четность: Периодичность:
Логарифмы и их свойства.
Его обычно называют основным логарифмическим тождеством. Свойства логарифмов.
1. 3. 5.
7.
9.
Формула перехода.
частные случаи: 1. 3. Десятичные логарифмы – логарифмы по основанию 10 числа а обозначают Натуральные логарифмы – логарифмы по основанию Геометрия.
Соотношения между элементами треугольника. 1. Теорема косинусов:
2. Теорема синусов: Свойства линий в треугольнике. Свойства медиан: пересекаются в одной точке; в точке пересечения делятся в отношении 2:1, считая от вершины; каждая медиана делит треугольник на два равновеликих треугольника. Свойства средней линии: равна половине параллельной ей стороны; отсекает треугольник с площадью равной одной четвертой площади треугольника. Свойства биссектрис: пересекаются в одной точке: если Свойство высот: пересекаются в одной точке;
Общие свойства многоугольников. 1. Сумма внутренних углов выпуклого n – угольника равна 2. Число всех диагоналей выпуклого n – угольника равно 3. Около выпуклого четырехугольника можно описать окружность, если сумма его противолежащих углов равна 4. В выпуклый четырехугольник можно вписать окружность, если суммы его противоположных сторон равны.
Основные формулы геометрии. Треугольник.
Прямоугольный треугольник.
Равносторонний треугольник.
Параллелограмм.
Ромб.
Прямоугольник.
Квадрат.
Трапеция.
Правильные многоугольники.
Окружность и круг.
S – площадь круга, R – радиус окружности (круга), L – длина окружности, l – длина дуги в Призма.
Прямоугольный параллелепипед.
Куб.
Пирамида.
l – апофема (высота боковой грани). Усеченная пирамида.
Тетраэдр.
Цилиндр.
Конус.
Усеченный конус.
L – образующая. Шар.
Шаровой сегмент.
Векторная алгебра.
Тогда: Модуль вектора Если точка точка
Скалярное произведение. Скалярное произведение векторов
Скалярное произведение в координатной записи:
Угол между двумя ненулевыми векторами, заданными своими координатами определяется формулой:
Необходимым и достаточным условием коллинеарности ненулевых векторов
Правила дифференцирования. Пусть 1. Производная постоянной равна нулю. 2. Производная суммы конечного числа функций равна сумме производных этих функций. 3. Производная произведения двух функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго. Следствие 1: Постоянный множитель можно выносить за знак производной. Следствие 2: Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные.
4. Производная частного двух дифференцируемых функций может быть найдена по формуле: Таблица производных. 1. 2. 3. 4. 5. 6. 7. 8. 9. Таблица интегралов. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 27. 28. Таблица квадратов натуральных чисел от 10 до 99.
Таблица квадратов и кубов натуральных чисел от 1 до 10 и степеней чисел 2 и 3.
|





















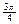





















 y
y  y
y III IV III IV
III IV III IV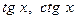 II I
II I (нечетная)
(нечетная) 
 (четная)
(четная) 
 (нечетная)
(нечетная) 
 (нечетная)
(нечетная) 
 Логарифмом числа b по основанию а называется показатель степени, в которую нужно возвести основание а, чтобы получить число b.
Логарифмом числа b по основанию а называется показатель степени, в которую нужно возвести основание а, чтобы получить число b. 

 ,
,  .
.
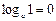 2.
2. 
 4.
4. 
 6.
6. 

 8.
8. 






 2.
2. 
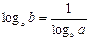 4.
4. 
 .
. обозначают
обозначают  .
.



 и
и 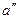 - отрезки, на которые делит сторону
- отрезки, на которые делит сторону  основание биссектрисы
основание биссектрисы  , то
, то  где
где  и
и  - стороны прилежащие к отрезкам
- стороны прилежащие к отрезкам 






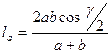
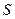 - площадь,
- площадь,  - стороны,
- стороны, 
 - высота, опущенная на сторону a, R – радиус описанной окружности, r – радиус вписанной окружности,
- высота, опущенная на сторону a, R – радиус описанной окружности, r – радиус вписанной окружности,  - полупериметр,
- полупериметр,  - угол между сторонами a и b,
- угол между сторонами a и b,  - медиана, проведенная к стороне a,
- медиана, проведенная к стороне a, - теорема Пифагора.
- теорема Пифагора.



 (свойство высоты)
(свойство высоты)  (свойство катетов)
(свойство катетов) - катеты, с – гипотенуза,
- катеты, с – гипотенуза,  - медиана, проведенная к гипотенузе,
- медиана, проведенная к гипотенузе,  - высота, опущенная на гипотенузу,
- высота, опущенная на гипотенузу,  - проекции катетов на гипотенузу.
- проекции катетов на гипотенузу.




 - диагонали,
- диагонали, 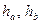 - высоты, опущенные на стороны a и b соответственно,
- высоты, опущенные на стороны a и b соответственно,  - угол между диагоналями.
- угол между диагоналями.

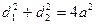






 l – средняя линия.
l – средняя линия.




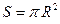



 - площадь сектора с центральным углом в
- площадь сектора с центральным углом в 

 (накл. пр.)
(накл. пр.)  (пр. призма)
(пр. призма) - периметр перпендикулярного сечения,
- периметр перпендикулярного сечения,  - длина бокового ребра.
- длина бокового ребра.







 - площади оснований,
- площади оснований,  - периметры оснований.
- периметры оснований.




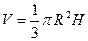





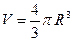
 S – площадь поверхности.
S – площадь поверхности.


 :
: 
 - начало,
- начало, - конец вектора
- конец вектора  , то
, то  и
и


 где
где  - угол между векторами
- угол между векторами 

 , что
, что 
 и
и  – две дифференцируемые функции.
– две дифференцируемые функции.






 11.
11. 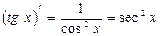
 12.
12. 
 13.
13. 
 14.
14. 
 15.
15. 
 16.
16. 
 17.
17. 
 18.
18. 
 14.
14. 
 15.
15. 
 16.
16. 
 17.
17. 
 18.
18. 
 19.
19. 
 20.
20. 
 21.
21. 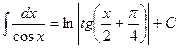
 22.
22. 
 23.
23. 
 24.
24. 
 25.
25. 
 26.
26. 









