1. Дана пара одноименных зарядов  и
и  , различных по величине. Расстояние между зарядами равно
, различных по величине. Расстояние между зарядами равно  . Определите расстояние от заряда
. Определите расстояние от заряда  , на котором следует поместить заряд
, на котором следует поместить заряд  , чтобы заряд
, чтобы заряд  был в равновесии.
был в равновесии.
А)  ; Б)
; Б)  ; В)
; В)  .
.
2. Сначала два маленький одинаковых шарика с зарядами  и
и  находятся на расстоянии
находятся на расстоянии  друг от друга. Потом их привели в соприкосновение и вновь развели на расстояние
друг от друга. Потом их привели в соприкосновение и вновь развели на расстояние  . Найдите электростатическую силу взаимодействия шариков до и после соприкосновения. Какая сила больше?
. Найдите электростатическую силу взаимодействия шариков до и после соприкосновения. Какая сила больше?
А)  ; Б)
; Б)  ; В)
; В)  .
.
3. Два одинаковых заряженных шара, наполненных гелием, соединены нитями длины  с грузом массы
с грузом массы  . Расстояние между центрами шаров равно
. Расстояние между центрами шаров равно  . Все параметры подобраны так, что шары парят в равновесии, удерживая груз. Считая, что оба шара несут одинаковый заряд
. Все параметры подобраны так, что шары парят в равновесии, удерживая груз. Считая, что оба шара несут одинаковый заряд  , определите его величину.
, определите его величину.
А)  ; Б)
; Б)  ; В)
; В)  .
.
4. Чему равна полная электростатическая сила, действующая на положительный заряд  , помещенный в центр квадрата со стороной
, помещенный в центр квадрата со стороной  , если по углам квадрата расположены заряды
, если по углам квадрата расположены заряды  ,
,  ,
,  и
и  ?
?
А)  ; Б) 0; В)
; Б) 0; В)  .
.
5. Определите, какую максимальную скорость разовьет заряженное тело, скользящее по наклонной плоскости в магнитном поле индукции 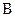 и в поле тяжести. Масса и заряд тела равны
и в поле тяжести. Масса и заряд тела равны  и
и  . Магнитное поле параллельно наклонной плоскости и перпендикулярно полю тяжести. Угол наклона плоскости к горизонту составляет
. Магнитное поле параллельно наклонной плоскости и перпендикулярно полю тяжести. Угол наклона плоскости к горизонту составляет  . Коэффициент трения о плоскость равен
. Коэффициент трения о плоскость равен  .
.
А)  ; Б)
; Б)  ; В)
; В) 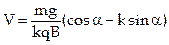 .
.
6. Система состоит из тонкого заряженного проволочного кольца радиуса  и очень длинной равномерно заряженной нити, расположенной по оси кольца так, что один из ее концов совпадает с центром кольца. Последнее имеет заряд
и очень длинной равномерно заряженной нити, расположенной по оси кольца так, что один из ее концов совпадает с центром кольца. Последнее имеет заряд  . Найдите силу взаимодействия кольца и нити.
. Найдите силу взаимодействия кольца и нити.
А)  ; Б)
; Б) 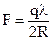 ; В)
; В)  .
.
7. Тонкое непроводящее кольцо радиуса  заряжено с линейной плотностью
заряжено с линейной плотностью  , где
, где  ,
,  − азимутальный угол. Найдите модуль напряженности электрического поля на оси кольца в зависимости от расстояния
− азимутальный угол. Найдите модуль напряженности электрического поля на оси кольца в зависимости от расстояния  до его центра.
до его центра.
А)  ; Б)
; Б)  ; В)
; В)  .
.
8. Найдите напряженность электрического поля в центре шара радиуса  , объемная плотность заряда которого
, объемная плотность заряда которого  , где
, где 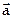 − постоянный вектор,
− постоянный вектор, 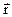 − радиус-вектор, проведенный из центра шара.
− радиус-вектор, проведенный из центра шара.
А)  ; Б)
; Б)  ; В)
; В)  .
.
9. Пространство заполнено зарядом с объемной плотностью  , где
, где  и
и  − положительные постоянные,
− положительные постоянные,  − расстояние от центра системы. Найдите модуль напряженности электрического поля, как функцию от
− расстояние от центра системы. Найдите модуль напряженности электрического поля, как функцию от  .
.
А)  ; Б)
; Б)  ; В)
; В)  .
.
10. Внутри шара, заряженного равномерно с объемной плотностью  , имеет сферическая полость. Центр полости смещен относительно центра шара на расстояние, характеризуемое вектором
, имеет сферическая полость. Центр полости смещен относительно центра шара на расстояние, характеризуемое вектором 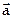 . Найти напряженность
. Найти напряженность  поля внутри полости.
поля внутри полости.
А)  ; Б)
; Б)  ; В)
; В)  .
.
11. Найдите напряженность электрического поля, потенциал которого имеет вид  , где
, где 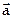 − некоторый постоянный вектор,
− некоторый постоянный вектор, 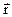 − радиус-вектор точки.
− радиус-вектор точки.
А)  ; Б)
; Б)  ; В)
; В)  .
.
12. Два одинаковых первоначально незаряженных плоских конденсатора с расстоянием между обкладками  вставлены друг в друга (см. рис. 1). При этом минимальное расстояние между пластинами, принадлежащими разным конденсаторам, равно
вставлены друг в друга (см. рис. 1). При этом минимальное расстояние между пластинами, принадлежащими разным конденсаторам, равно  . Потом к каждому из конденсаторов подключили источники питания, создавшие между обкладками напряжение
. Потом к каждому из конденсаторов подключили источники питания, создавшие между обкладками напряжение  и
и  . Определите разность потенциалов между внутренними пластинами 3 и 2.
. Определите разность потенциалов между внутренними пластинами 3 и 2.
А) 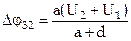 ; Б)
; Б)  ; В)
; В)  .
.
13. Ток  течет по длинному прямому проводнику, сечение которого имеет форму тонкого полукольца радиуса течет по длинному прямому проводнику, сечение которого имеет форму тонкого полукольца радиуса  . Найдите индукцию магнитного поля в точке O, лежащей на его оси в плоскости сечения.
А) . Найдите индукцию магнитного поля в точке O, лежащей на его оси в плоскости сечения.
А)  ; Б) ; Б)  ; В) ; В)  .
14. Определите индукцию магнитного поля тока, распределенного равномерно по двум параллельным плоскостям с линейными плотностями .
14. Определите индукцию магнитного поля тока, распределенного равномерно по двум параллельным плоскостям с линейными плотностями  и и  , между плоскостями. , между плоскостями.
| 
|
| Рис. 1
|
А) 0; Б)  ; В)
; В)  .
.
15. Для кругового витка с током I вычислите интеграл  в пределах от
в пределах от  до
до  . Что это значит?
. Что это значит?
А)  ; Б)
; Б)  ; В) 0.
; В) 0.
16. Найдите плотность тока как функцию расстояния  от оси аксиально-симметричного параллельного потока электронов, если индукция магнитного поля внутри потока зависит от
от оси аксиально-симметричного параллельного потока электронов, если индукция магнитного поля внутри потока зависит от  по закону
по закону  , где
, где  и
и  − положительные постоянные.
− положительные постоянные.
А)  ; Б)
; Б)  ; В)
; В)  .
.
17. Вычислите магнитный момент тонкого проводника с током I, плотно навитого на половину тора. Диаметр сечения тора d, число витков N.
А)  ; Б)
; Б)  ; В)
; В)  .
.
18. В поле длинного прямого провода с током  находится контур с током находится контур с током  (рис. 2). Найти момент сил Ампера, действующих на этот контур. Необходимые размеры системы указаны на рисунке.
А) (рис. 2). Найти момент сил Ампера, действующих на этот контур. Необходимые размеры системы указаны на рисунке.
А)  ; Б) ; Б)  ; В) ; В)  .
19. Точечный сторонний заряд .
19. Точечный сторонний заряд  находится в центре диэлектрического шара радиуса находится в центре диэлектрического шара радиуса  с проницаемостью с проницаемостью  . Шар окружен безгранич- . Шар окружен безгранич-
| 
|
| Рис. 2
|
ным диэлектриком с проницаемостью  . Найдите поверхностную плотность связанных зарядов на границе раздела этих диэлектриков.
. Найдите поверхностную плотность связанных зарядов на границе раздела этих диэлектриков.
А)  ; Б)
; Б)  ; В)
; В)  .
.
20. Точечный сторонний заряд  находится в центре сферического слоя неоднородного изотропного диэлектрика, проницаемость которого изменяется только в радиальном направлении по закону
находится в центре сферического слоя неоднородного изотропного диэлектрика, проницаемость которого изменяется только в радиальном направлении по закону  , где
, где  − постоянная,
− постоянная,  − расстояние от центра системы. Найдите объемную плотность
− расстояние от центра системы. Найдите объемную плотность  связанных зарядов как функцию
связанных зарядов как функцию  внутри слоя.
внутри слоя.
А)  ; Б)
; Б)  ; В)
; В)  .
.
21. Прямой бесконечно длинный проводник с током  лежит в плоскости двух непроводящих сред с магнитными проницаемостями
лежит в плоскости двух непроводящих сред с магнитными проницаемостями 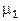 и
и  . Найдите модуль вектора индукции магнитного поля во всем пространстве в зависимости от расстояния
. Найдите модуль вектора индукции магнитного поля во всем пространстве в зависимости от расстояния  до провода. Необходимо считать, что линии вектора
до провода. Необходимо считать, что линии вектора  являются окружностями с центром на оси провода.
являются окружностями с центром на оси провода.
А)  ; Б)
; Б)  ; В)
; В)  .
.
22. Если шар из однородного магнетика поместить во внешнее однородное магнитное поле с индукцией 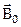 , он намагнититься однородно. Найдите индукцию внутри шара с магнитной проницаемостью
, он намагнититься однородно. Найдите индукцию внутри шара с магнитной проницаемостью  , имея в виду, что в случае однородного намагничивания шара магнитное поле внутри него является однородным и его напряженность
, имея в виду, что в случае однородного намагничивания шара магнитное поле внутри него является однородным и его напряженность  , где
, где  − намагниченность.
− намагниченность.
А)  ; Б)
; Б)  ; В)
; В)  .
.
23. Тонкое проволочное кольцо радиуса  имеет заряд
имеет заряд  . Кольцо расположено параллельно проводящей плоскости на расстоянии
. Кольцо расположено параллельно проводящей плоскости на расстоянии  от нее. Найдите поверхностную плотность индуцированного заряда в точках плоскости, расположенных симметрично относительно кольца.
от нее. Найдите поверхностную плотность индуцированного заряда в точках плоскости, расположенных симметрично относительно кольца.
А)  ; Б)
; Б)  ; В)
; В)  .
.
24. Сколько теплоты выделится при переключении ключа из положения 1 в 2 в цепи на рис. 3?
А)  ; Б)
; Б)  ; В)
; В)  .
.
25. Найдите значение силы тока, текущего через резистор с сопротивлением  в схеме на рис. 4, если
в схеме на рис. 4, если  В,
В,  В,
В,  Ом,
Ом,  Ом,
Ом,  Ом.
Ом.
А)  ; Б)
; Б)  ; В)
; В)  .
.
26. Определите ток, текущий через идеальный диод в цепи, изображенной на рис. 5. Пусть  В,
В,  кОм,
кОм,  кОм,
кОм,  кОм,
кОм,  кОм.
кОм.
А) 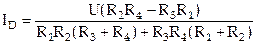 ; Б)
; Б)  ; В) 0.
; В) 0.
27. При каком сопротивлении  в цепочке (рис. 6) сопротивление между точками А и В не зависит от числа ячеек, образованных повторением резисторов R и 2R?
в цепочке (рис. 6) сопротивление между точками А и В не зависит от числа ячеек, образованных повторением резисторов R и 2R?
А)  ; Б)
; Б)  ; В)
; В)  .
.

| 
| 
|
| Рис. 3.
| Рис. 4.
| Рис. 5.
|

|
| Рис. 6.
|
28. Квадратная рамка со стороной  и длинный прямой провод с током
и длинный прямой провод с током  находятся в одной плоскости: рамка лежит справа от провода. Рамку поступательно перемещают вправо с постоянной скоростью
находятся в одной плоскости: рамка лежит справа от провода. Рамку поступательно перемещают вправо с постоянной скоростью  . Найдите э.д.с. индукции в рамке как функцию расстояния
. Найдите э.д.с. индукции в рамке как функцию расстояния  от провода.
от провода.
А)  ; Б)
; Б)  ; В)
; В)  .
.
29. Квадратная проволочная рамка со стороной  и прямой длинный проводник с постоянным током
и прямой длинный проводник с постоянным током  лежат в одной плоскости: рамка лежит справа от провода так, что ее сторона параллельна проводу. Индуктивность рамки
лежат в одной плоскости: рамка лежит справа от провода так, что ее сторона параллельна проводу. Индуктивность рамки  , сопротивление
, сопротивление  . Рамку повернули на 1800 вокруг дальней стороны, которая параллельна проводу, и остановили (расстояние от провода до этой стороны равно
. Рамку повернули на 1800 вокруг дальней стороны, которая параллельна проводу, и остановили (расстояние от провода до этой стороны равно  ). Найдите заряд, протекший при этом по рамке.
). Найдите заряд, протекший при этом по рамке.
А)  ; Б)
; Б)  ; В)
; В)  .
.
30. В схеме, изображенной на рис. 7, известны э.д.с. источника  , его внутреннее сопротивление , его внутреннее сопротивление  и индуктивности и индуктивности 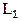 и и  . Найдите установившиеся токи в катушке . Найдите установившиеся токи в катушке 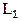 после замыкания ключа К.
А) после замыкания ключа К.
А)  ; Б) ; Б)  ; В) ; В)  . .
| 
|
| Рис. 7.
|
Ключ к тесту:
| Вопрос
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ответ
| А
| Б
| А
| В
| Б
| В
| А
| Б
| В
| А
| В
| А
| А
| Б
| Б
| В
| Б
| А
| В
| А
| Б
| Б
| В
| В
| А
| А
| В
| Б
| А
| А
|
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА

 и
и  , различных по величине. Расстояние между зарядами равно
, различных по величине. Расстояние между зарядами равно  . Определите расстояние от заряда
. Определите расстояние от заряда  , чтобы заряд
, чтобы заряд  ; Б)
; Б)  ; В)
; В)  .
. ; Б)
; Б)  ; В)
; В)  .
. с грузом массы
с грузом массы  . Расстояние между центрами шаров равно
. Расстояние между центрами шаров равно  , определите его величину.
, определите его величину. ; Б)
; Б)  ; В)
; В)  .
. , помещенный в центр квадрата со стороной
, помещенный в центр квадрата со стороной  , если по углам квадрата расположены заряды
, если по углам квадрата расположены заряды  ,
,  и
и  ; Б) 0; В)
; Б) 0; В)  .
.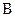 и в поле тяжести. Масса и заряд тела равны
и в поле тяжести. Масса и заряд тела равны  . Коэффициент трения о плоскость равен
. Коэффициент трения о плоскость равен  .
. ; Б)
; Б)  ; В)
; В) 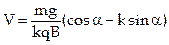 .
. и очень длинной равномерно заряженной нити, расположенной по оси кольца так, что один из ее концов совпадает с центром кольца. Последнее имеет заряд
и очень длинной равномерно заряженной нити, расположенной по оси кольца так, что один из ее концов совпадает с центром кольца. Последнее имеет заряд  ; Б)
; Б) 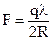 ; В)
; В)  .
. , где
, где  ,
,  − азимутальный угол. Найдите модуль напряженности электрического поля на оси кольца в зависимости от расстояния
− азимутальный угол. Найдите модуль напряженности электрического поля на оси кольца в зависимости от расстояния  до его центра.
до его центра. ; Б)
; Б)  ; В)
; В)  .
. , где
, где 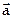 − постоянный вектор,
− постоянный вектор, 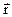 − радиус-вектор, проведенный из центра шара.
− радиус-вектор, проведенный из центра шара. ; Б)
; Б)  ; В)
; В)  .
. , где
, где  и
и  ; Б)
; Б)  ; В)
; В)  .
. , имеет сферическая полость. Центр полости смещен относительно центра шара на расстояние, характеризуемое вектором
, имеет сферическая полость. Центр полости смещен относительно центра шара на расстояние, характеризуемое вектором  поля внутри полости.
поля внутри полости. ; Б)
; Б)  ; В)
; В)  .
. , где
, где  ; Б)
; Б)  ; В)
; В)  .
. вставлены друг в друга (см. рис. 1). При этом минимальное расстояние между пластинами, принадлежащими разным конденсаторам, равно
вставлены друг в друга (см. рис. 1). При этом минимальное расстояние между пластинами, принадлежащими разным конденсаторам, равно  . Потом к каждому из конденсаторов подключили источники питания, создавшие между обкладками напряжение
. Потом к каждому из конденсаторов подключили источники питания, создавшие между обкладками напряжение  и
и  . Определите разность потенциалов между внутренними пластинами 3 и 2.
. Определите разность потенциалов между внутренними пластинами 3 и 2.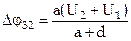 ; Б)
; Б)  ; В)
; В)  .
. течет по длинному прямому проводнику, сечение которого имеет форму тонкого полукольца радиуса
течет по длинному прямому проводнику, сечение которого имеет форму тонкого полукольца радиуса  ; Б)
; Б)  ; В)
; В)  .
14. Определите индукцию магнитного поля тока, распределенного равномерно по двум параллельным плоскостям с линейными плотностями
.
14. Определите индукцию магнитного поля тока, распределенного равномерно по двум параллельным плоскостям с линейными плотностями  и
и  , между плоскостями.
, между плоскостями.

 ; В)
; В)  .
. в пределах от
в пределах от  до
до  . Что это значит?
. Что это значит? ; Б)
; Б)  ; В) 0.
; В) 0. , где
, где  ; Б)
; Б)  ; В)
; В)  .
. ; Б)
; Б)  ; В)
; В)  .
. находится контур с током
находится контур с током  ; Б)
; Б)  ; В)
; В)  .
19. Точечный сторонний заряд
.
19. Точечный сторонний заряд  . Шар окружен безгранич-
. Шар окружен безгранич-

 . Найдите поверхностную плотность связанных зарядов на границе раздела этих диэлектриков.
. Найдите поверхностную плотность связанных зарядов на границе раздела этих диэлектриков. ; Б)
; Б)  ; В)
; В)  .
. , где
, где  связанных зарядов как функцию
связанных зарядов как функцию  ; Б)
; Б)  ; В)
; В)  .
.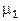 и
и  . Найдите модуль вектора индукции магнитного поля во всем пространстве в зависимости от расстояния
. Найдите модуль вектора индукции магнитного поля во всем пространстве в зависимости от расстояния  являются окружностями с центром на оси провода.
являются окружностями с центром на оси провода. ; Б)
; Б)  ; В)
; В)  .
.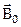 , он намагнититься однородно. Найдите индукцию внутри шара с магнитной проницаемостью
, он намагнититься однородно. Найдите индукцию внутри шара с магнитной проницаемостью  , имея в виду, что в случае однородного намагничивания шара магнитное поле внутри него является однородным и его напряженность
, имея в виду, что в случае однородного намагничивания шара магнитное поле внутри него является однородным и его напряженность  , где
, где  − намагниченность.
− намагниченность. ; Б)
; Б)  ; В)
; В)  .
. ; Б)
; Б)  ; В)
; В)  .
. ; Б)
; Б)  ; В)
; В)  .
. В,
В,  В,
В,  Ом,
Ом,  Ом,
Ом,  Ом.
Ом. ; Б)
; Б)  ; В)
; В)  .
. В,
В,  кОм,
кОм,  кОм,
кОм,  кОм,
кОм,  кОм.
кОм.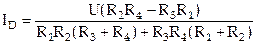 ; Б)
; Б)  ; В) 0.
; В) 0. в цепочке (рис. 6) сопротивление между точками А и В не зависит от числа ячеек, образованных повторением резисторов R и 2R?
в цепочке (рис. 6) сопротивление между точками А и В не зависит от числа ячеек, образованных повторением резисторов R и 2R? ; Б)
; Б)  ; В)
; В)  .
.



 . Найдите э.д.с. индукции в рамке как функцию расстояния
. Найдите э.д.с. индукции в рамке как функцию расстояния  ; Б)
; Б)  ; В)
; В)  .
. , сопротивление
, сопротивление  ; Б)
; Б)  ; В)
; В)  .
. , его внутреннее сопротивление
, его внутреннее сопротивление 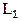 и
и  . Найдите установившиеся токи в катушке
. Найдите установившиеся токи в катушке  ; Б)
; Б)  ; В)
; В)  .
.




