Тема 4. Метод наименьших квадратов
Нормальная система уравнений для определения параметров
4.1. Методом наименьших квадратов найти параметр 1)
2)
4.2. Результаты измерений величин 1)
2)
3)
Модуль 3. НЕОПРЕДЕЛЕННЫЙ И ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛЫ
Тема 1. Неопределенный интеграл, его свойства и вычисление Понятие неопределенного интеграла
1.1. Проверить правильность интегрирования.
Непосредственное интегрирование 1.2. Вычислить интегралы, используя свойства и таблицу основных интегралов.
9) 12) 15) 17)
Замена переменной в неопределенном интеграле
2.1. Найти интегралы методом замены переменной 1) 4) 7) 10) 13) 16) 19); 20); 21).
Метод интегрирования по частям 2.2. С помощью метода интегрирования по частям найти интегралы. 1) 4); 5); 6).
Тема 2. Интегрирование рациональных функций
Интегралы от рациональных дробей 3.1. Найти интегралы. 1); 2); 3); 4).
Интегралы от рациональной дроби 3.2. Найти интегралы. 1); 2); 3). Интегралы от правильной дробно-рациональной функции 3.3. Найти интегралы, используя метод неопределенных коэффициентов. 1) 4); 5); 6); 7).
Интегралы от неправильной дробно-рациональной функции 3.4. Найти интегралы. 1) 4); 5); 6).
|

 и
и  эмпирической формулы
эмпирической формулы 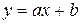 :
:
 между величинами по результатам измерений. Построить эмпирические точки
между величинами по результатам измерений. Построить эмпирические точки  и прямую, выражаемую найденной приближенной формулой
и прямую, выражаемую найденной приближенной формулой 
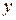
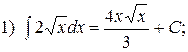 2)
2)  ;
;

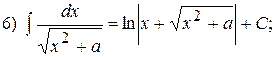

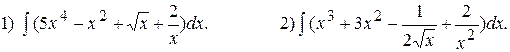

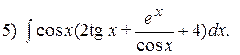

 ; 8)
; 8)  ;
; ; 10)
; 10)  ; 11)
; 11)  ;
; ; 13)
; 13)  ; 14)
; 14)  ;
; ; 16)
; 16) 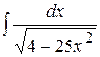 ;
; ; 18)
; 18)  ; 19)
; 19)  .
. ; 2)
; 2)  ; 3)
; 3)  ;
; ; 5)
; 5)  ; 6)
; 6)  ;
; ; 8)
; 8)  ;
; ;
;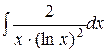 ; 14)
; 14)  ; 15)
; 15)  ;
; ; 17)
; 17)  ; 18)
; 18)  ;
;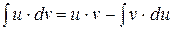 .
.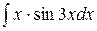 ; 2)
; 2) 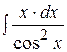 ; 3)
; 3)  ;
; и
и 
 (
( )
)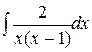 ; 2)
; 2) 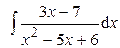 ; 3)
; 3)  ;
; ; 2)
; 2)  ; 3)
; 3)  ;
;


