Тема 4. Производные и дифференциалы функции
Результаты химико-токсикологического анализа позволили обнаружить в биообъектах. . .
Эксперт-химик. Подпись. «_____»20 г. Модуль 1. дифференциальное исчисление функции одной переменной
Тема 1. функции одной переменной, свойства и графики Функции одной переменной 1.1. Найти и построить область определения функций одной переменной. а) г) 1.2. Установить, является ли функция четной или нечетной. а) д) 1.3. По заданным функциям
1.4. Построить графики функций с помощью геометрических преобразований графиков основных элементарных функций (сдвиг, растяжение и сжатие по осям). 1) 3) 5) 7) 9) 11) 13) Тема 2. Предел функции
Вычисление предела 2.1. Вычислить пределы функций при 1) 4); 5); 6); 7). 2.2. Вычислить пределы функций при 1) 3); 4). Первый замечательный предел 2.3. Используя первый замечательный предел, вычислить пределы.
Второй замечательный предел 2.3. Используя второй замечательный предел, вычислить пределы. 1) 4); 5); 6).
Тема 3. Непрерывные функции
Точки разрыва функции 3.1. Найти точки разрыва функции
Непрерывность функции на отрезке 3.2. Исследовать на непрерывность функцию Характер точек разрыва 3.3. Определить характер точек разрыва функции.
Тема 4. Производные и дифференциалы функции
Вычисление производных 4.1. Вычислить производные.
4.2. Вычислить производные.
Производные сложных функций 4.3. Пользуясь правилом дифференцирования сложной функции, найти производные функций. 1) 4) 7) 10) Касательная к графику функции 4.4. Составить уравнения касательных к графикам функций: 1) y = x2 - 3x + 2 в точке (3;2). 2) y = 3) y = ln x в точке пересечения с осью Оx. 4) y = x2 - 5x + 6 в точках пересечения с осью Оx. 5) y = e7x в точке пересечения с осью Оy. Производные высших порядков 4.5. Найти производные 2-го порядка от функций: 1) 5.6. Найти производные n-го порядка от функций: 1) y = Вычисление пределов с помощью производных (правило Лопиталя) 4.7. Найти пределы с помощью правила Лопиталя: 1) 5) Понятие дифференциала 4.8. Найти дифференциалы функций: 1) y = x3 – 3ln x; 2) y = 5) y = x2 arctg x; 6) y = 4.9. Найти приближенно приращение 1) функции у = 2) функции у = sinx, если х =
Дифференциал второго порядка 4.10. Найти дифференциалы 2-го порядка от функций: 1) y = x3 – 3x2 + x + 1; 2) y = (0,1x+1)5; 3) y = xcos2x; 4) y = sin2x.
Вычисление пределов с помощью производных (правило Лопиталя) 4.10. Найти пределы с помощью правила Лопиталя: 1) 5)
|

 ; б)
; б)  ; в)
; в)  ;
; ; д)
; д)  ; е)
; е)  .
.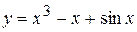 ; б)
; б)  ; в)
; в)  ; г)
; г)  ,
, .
.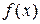 и
и  построить сложную функцию
построить сложную функцию 

 ; 2)
; 2)  ;
; ; 4)
; 4)  ;
; ; 6)
; 6)  ;
; ; 8)
; 8)  ;
; ; 10)
; 10)  ;
; ; 12)
; 12)  ;
;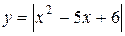
 .
. ; 2)
; 2)  ; 3)
; 3) 
 ;
; .
.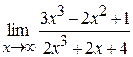 ; 2)
; 2)  ;
;
 ж)
ж)  ; з)
; з)  ; и)
; и)  .
.
 ; 2)
; 2)  ; 3)
; 3)  ;
;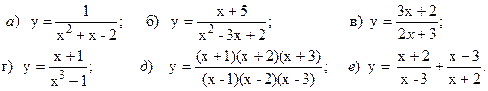
 на отрезке:
на отрезке: 



 ; 2)
; 2)  ; 3)
; 3)  ;
; ; 5)
; 5)  ; 6)
; 6)  ;
; ; 8)
; 8) 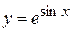 ; 9)
; 9)  ;
; .
. в точке (4;2).
в точке (4;2). ; 2)
; 2)  ; 3)
; 3) 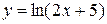 ; 4)
; 4) 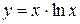 .
. ; 2) y = e2x; 3) y = 5x; 4) y = ln(1+x).
; 2) y = e2x; 3) y = 5x; 4) y = ln(1+x). ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 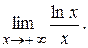 ;
; ; 6)
; 6)  ; 7)
; 7) 
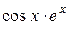 ; 3) y = sin 3x; 4) y = tg ln x.;
; 3) y = sin 3x; 4) y = tg ln x.; ; 7) y =
; 7) y =  ; 8) y =
; 8) y =  .
.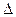 у:
у: , если х = 4,
, если х = 4,  ,
,  ;
;


