Тема 5. Исследование поведения функции с помощью производных
Экстремум функции 5.1. Определить интервалы монотонности и исследовать на экстремум функции. 1) 3) Наибольшее и наименьшее значения функции 5.2. Найти наибольшее и наименьшее значения функции на отрезке. 1) 3) Интервалы выпуклости и точки перегиба графиков функций 5.3. Найти промежутки выпуклости и точки перегиба графика функции. 1) 3)
Асимптоты графиков функций 5.4. Найти все асимптоты графиков функций. 1); 2); 3); 4). Исследование функции и построение графика 5.5. Провести полное исследование поведения функции и построить график. 1) 5); 6); 7); 8). 5.6. Постройте на отрезке [0;6] график функции
Модуль 2. Дифференциальное исчисление функции нескольких переменных Тема 1. Функции двух переменных Область определения функции двух переменных 1.1. Найти значения функции при заданных значениях аргументов. 1) 2) 3);,. 1.2. Найти и построить область определения функции двух переменных. 1) Частные и полное приращения 1.3. Дана функция Найти частные приращения при переходе от точки Найти полное приращение при переходе от точки Линии уровня 1.4. Построить линии уровня функции двух переменных 1) 2) 3),. Частные производные первого порядка 1.5. Найти частные производные 1-го порядка функции: 1) 4) 7) 10). 1.6. Вычислить значения частных производных функции в точке. 1),; 2),. Полный дифференциал и полное приращение функции 1.7. Найти полный дифференциал и вычислить его в точке 1); 2). 1.8. Вычислить приближенно выражение, заменяя приращение функции дифференциалом. 1); 2). Градиент функции 1.9. Найти градиент 1) 1.10. Построить линии уровня и 1); 2); 3). Частные производные и дифференциалы второго порядка 1.11. Найти частные производные второго порядка. Убедиться в равенстве смешанных частных производных. 1) 4); 5). 1.12. Найти дифференциал второго порядка 1); 2); 3).
|

 ; 2)
; 2) 
 ; 4)
; 4)  .
. на отрезке [0;2]; 2)
на отрезке [0;2]; 2)  на отрезке [-3;0];
на отрезке [-3;0];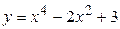 на отрезке
на отрезке  ; 4)
; 4)  на отрезке
на отрезке  .
. ; 2)
; 2)  ;
; ; 4)
; 4)  .
. ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ;
; , если:
, если:
 ,
,  ,
,  ;
;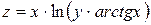 ,
,  ,
,  ;
; ; 2)
; 2) 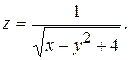 ; 3)
; 3) 
 .
. соответственно к точкам
соответственно к точкам  ,
, 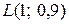 .
. .
. при заданных значениях
при заданных значениях 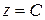 .
. ,
,  ;
; ,
,  ;
; ; 2)
; 2)  ; 3)
; 3)  ;
; ; 5)
; 5)  ; 6)
; 6)  ;
; ; 8)
; 8)  ; 9)
; 9)  ;
; .
. функции:
функции: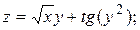 2)
2)  3)
3) 
 ; 2)
; 2)  ; 3)
; 3)  ;
; для функций.
для функций.


